Bootstrap

《PyTorch 深度学习实践》第12讲 循环神经网络（基础篇）

文章目录

该专栏内容为对该视频的学习记录：【《PyTorch深度学习实践》完结合集】
专栏的全部代码、数据集和课件全放在个人GitHub了，欢迎自取。

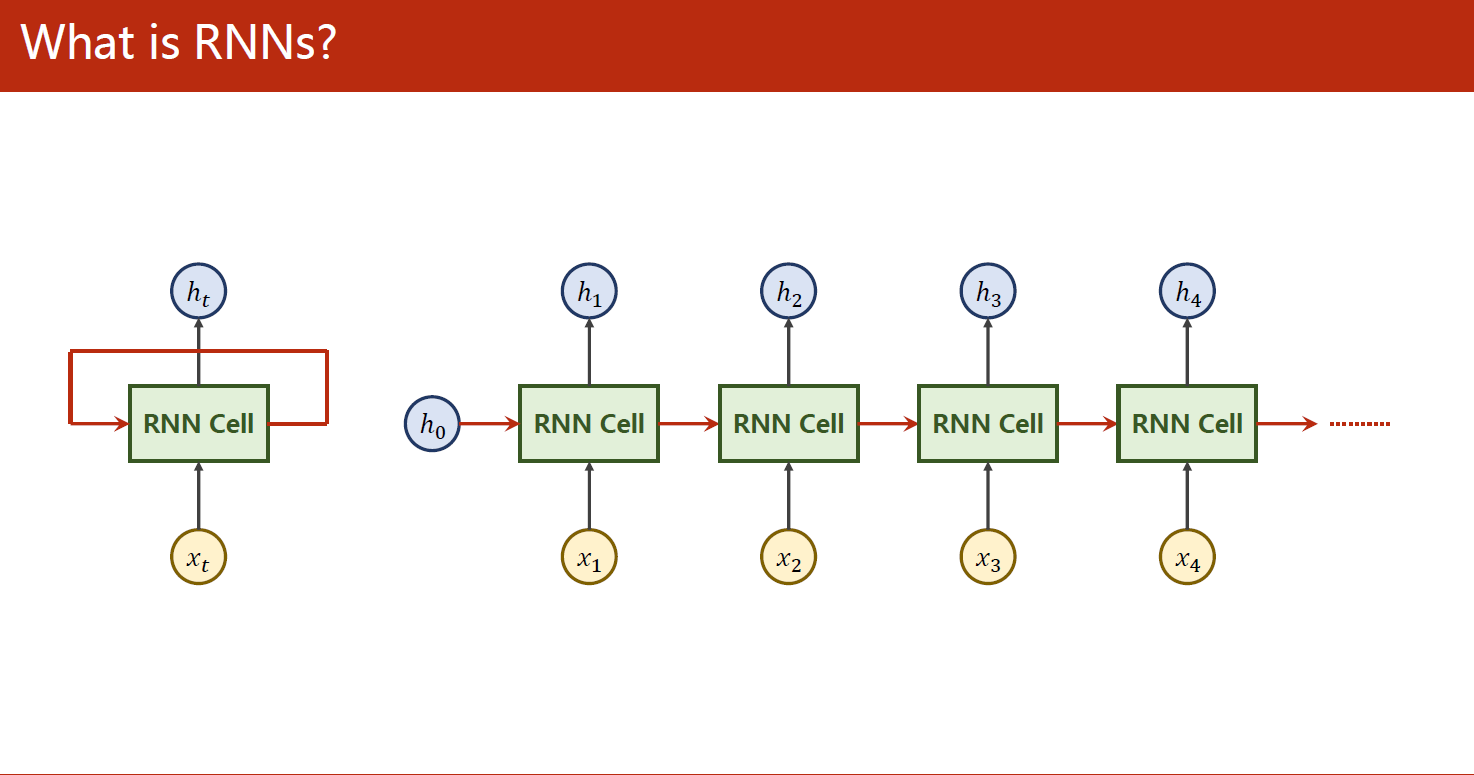
1 什么是RNN？

RNN是循环神经网络（Recurrent Neural Network）的缩写。它是一种神经网络结构，可以处理序列数据，例如时间序列数据或自然语言文本数据。相比于传统的前馈神经网络，RNN可以利用当前的输入和之前的状态来决定当前的输出，因此它可以捕捉到序列数据中的时间依赖关系。

在RNN中，每个时间步都有一个隐藏状态（hidden state），这个隐藏状态可以捕捉到之前时间步的信息，并且会在当前时间步中被用于计算输出。RNN的训练过程通常使用反向传播算法和梯度下降优化算法，目标是最小化模型预测值和真实值之间的误差。

RNN在自然语言处理、语音识别、时间序列预测等领域都有广泛的应用。

image-20230423123352273

1.1 原理

RNN的核心思想是利用当前的输入和之前的状态来决定当前的输出，这使得RNN可以处理序列数据中的时间依赖关系。RNN的结构可以看作是在时间轴上展开的多个神经网络层，每个时间步都有一个隐藏状态，这个隐藏状态可以传递到下一个时间步，并参与当前时间步的计算。

image-20230423123912734

具体来说，RNN的计算可以分为三个步骤：

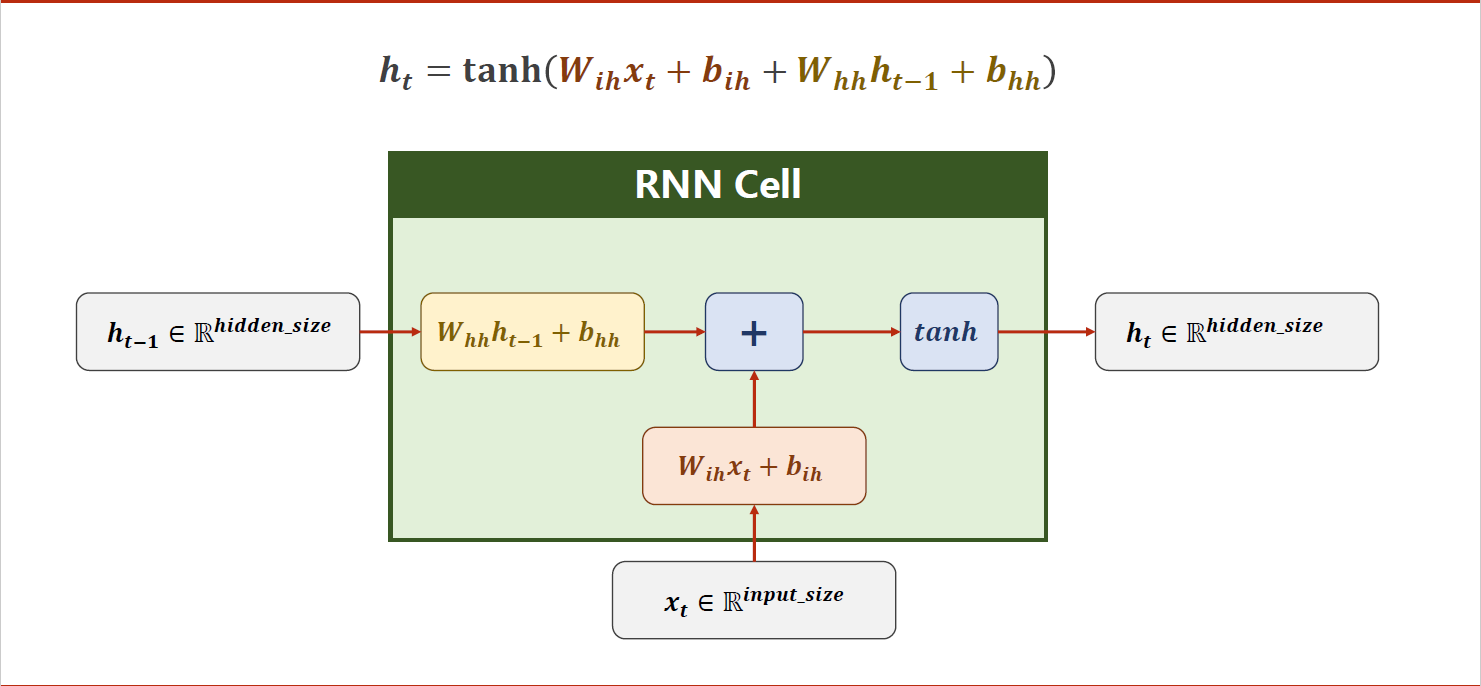
  1. 输入层和隐藏层之间的计算。假设当前时间步的输入是 x t x_t xt​，上一个时间步的隐藏状态是 h t − 1 h_{t-1} ht−1​，那么当前时间步的隐藏状态 h t h_t ht​可以通过下面的公式计算得到：

h t = f ( W i h x t + b i h + W h h h t − 1 + b h h ) h_t = f(W_{ih} x_t + b_{ih} + W_{hh} h_{t-1} + b_{hh}) ht​=f(Wih​xt​+bih​+Whh​ht−1​+bhh​)

其中 W i h W_{ih} Wih​是输入层到隐藏层的权重矩阵， W h h W_{hh} Whh​是隐藏层到隐藏层的权重矩阵， b i h b_{ih} bih​和 b h h b_{hh} bhh​是隐藏层的偏置向量， f f f是激活函数（通常是tanh或ReLU，上图中是tanh，即双曲正切函数）。

  1. 隐藏层和输出层之间的计算。假设当前时间步的隐藏状态是 h t h_t ht​，那么当前时间步的输出 y t y_t yt​可以通过下面的公式计算得到：

y t = g ( W h y h t + b y ) y_t=g(W_{hy}h_t+b_y) yt​=g(Why​ht​+by​)

其中 W h y W_{hy} Why​是隐藏层到输出层的权重矩阵， b y b_y by​是输出层的偏置向量， g g g是输出层的激活函数（通常是softmax）。

  1. 损失函数计算和反向传播。根据任务类型，可以选择不同的损失函数，例如交叉熵损失函数用于分类任务，均方误差损失函数用于回归任务。然后使用反向传播算法和梯度下降优化算法来更新权重和偏置，目标是最小化模型预测值和真实值之间的误差。

RNN的主要优点是可以处理任意长度的序列数据，并且可以捕捉序列数据中的时间依赖关系。然而，RNN也存在一些缺点，例如难以处理长期依赖关系、训练速度慢、梯度消失和梯度爆炸等问题。因此，研究人员提出了许多改进的RNN模型，例如LSTM和GRU等。

1.2 维度说明

在RNN中，输入、输出和隐藏层的维度可以根据具体的应用场景和数据集来确定。通常情况下，输入和输出的维度是固定的，而隐藏层的维度则是由用户自己指定的超参数。

以下是一些常见的维度配置：

  1. 序列分类任务中，输入通常是一个序列的特征向量，输出是一个类别标签。假设输入序列的长度为seq_len，每个时间步的特征向量维度为input_size，输出类别数为num_classes，那么输入和输出的维度分别为[batch_size, seq_len, input_size]和[batch_size, num_classes]，其中batch_size为批次大小。
  2. 序列生成任务中，输入和输出都是一个序列。假设输入序列的长度为seq_len，每个时间步的特征向量维度为input_size，输出序列的长度也为seq_len，每个时间步的特征向量维度为output_size，那么输入和输出的维度都为[batch_size, seq_len, input_size]或[batch_size, seq_len, output_size]，具体要看是什么任务。
  3. 序列标注任务中，输入通常是一个序列的特征向量，输出是每个时间步的标注信息。假设输入序列的长度为seq_len，每个时间步的特征向量维度为input_size，输出标注类别数为num_classes，那么输入和输出的维度分别为[batch_size, seq_len, input_size]和[batch_size, seq_len, num_classes]。
  4. 在隐藏层维度方面，可以根据任务和数据集的复杂程度来选择合适的值。一般来说，隐藏层的维度越大，模型的表达能力就越强，但也会增加模型的计算复杂度和训练难度。通常情况下，隐藏层的维度在几十到几百之间。

2 一些琐碎代码

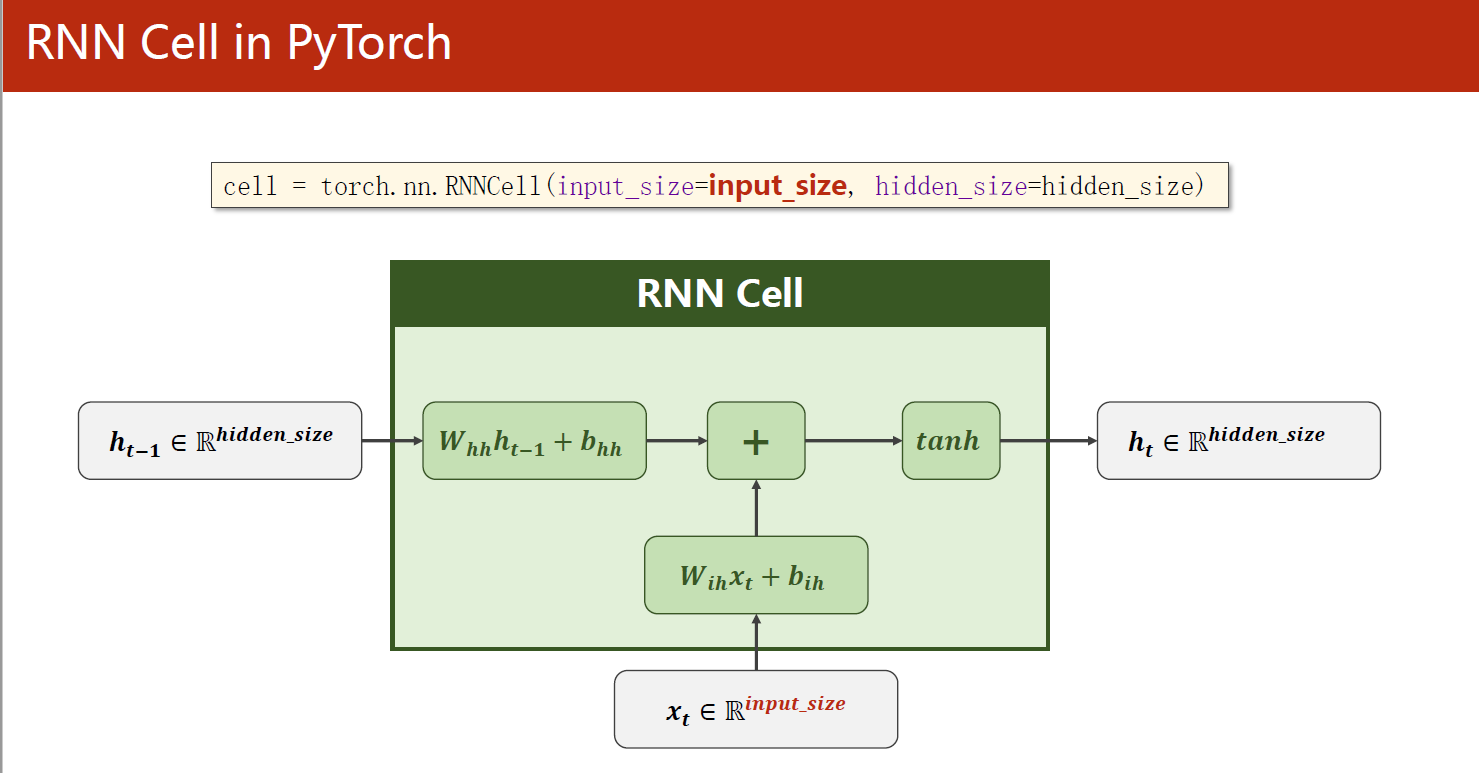
2.1 RNNCell

image-20230423130301157

这段代码演示了如何使用PyTorch的RNNCell模块构建一个简单的RNN，并对一个简单的序列进行前向传递计算。

在代码中，我们首先构建了一个RNNCell对象，使用了输入维度为input_size、输出维度为hidden_size的隐藏层。接着，我们构造了一个大小为(seq_len, batch_size, input_size)的输入数据集dataset，并将隐藏状态hidden初始化为全零张量，大小为(batch_size, hidden_size)。

然后，我们将数据集按序列长度依次输入到RNNCell中，并在每一步更新隐藏状态hidden。在每一步中，我们打印出隐藏状态hidden的形状和值，以便了解RNN在每个时间步的输出情况。

具体来说，循环从seq_len的第0个时间步开始，依次将大小为(batch_size, input_size)的输入数据input输入到RNNCell中，并用当前的隐藏状态hidden计算下一个隐藏状态。由于这是一个简单的循环，每次更新隐藏状态时，输出的hidden大小保持不变，都是(batch_size, hidden_size)。

代码如下：

import torch

batch_size = 1
seq_len = 3
input_size = 4
hidden_size = 2

# Construction of RNNCell
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)
# Wrapping the sequence into:(seqLen,batchSize,InputSize)
dataset = torch.randn(seq_len, batch_size, input_size)  # (3,1,4)
# Initializing the hidden to zero
hidden = torch.zeros(batch_size, hidden_size)  # (1,2)

for idx, input in enumerate(dataset):
    print('=' * 20, idx, '=' * 20)  #分割线，20个=号
    print('Input size:', input.shape)  # (batch_size, input_size)
    # 按序列依次输入到cell中，seq_len=3，故循环3次
    hidden = cell(input, hidden)  # 返回的hidden是下一次的输入之一，循环使用同一个cell

    print('output size:', hidden.shape)  # (batch_size, hidden_size)
    print(hidden)

运行结果：

==================== 0 ====================
Input size: torch.Size([1, 4])
output size: torch.Size([1, 2])
tensor([[-0.4140,  0.1517]], grad_fn=<TanhBackward0>)
==================== 1 ====================
Input size: torch.Size([1, 4])
output size: torch.Size([1, 2])
tensor([[-0.4725, -0.7875]], grad_fn=<TanhBackward0>)
==================== 2 ====================
Input size: torch.Size([1, 4])
output size: torch.Size([1, 2])
tensor([[-0.8257, -0.2262]], grad_fn=<TanhBackward0>)

可以看到，每次计算后的隐藏状态hidden都是2维的张量，大小为(batch_size, hidden_size) = (1, 2)。在每个时间步骤中，输出的hidden值都不同，因为输入数据集dataset不同，而隐藏状态hidden是随着时间步骤的推进而更新的。

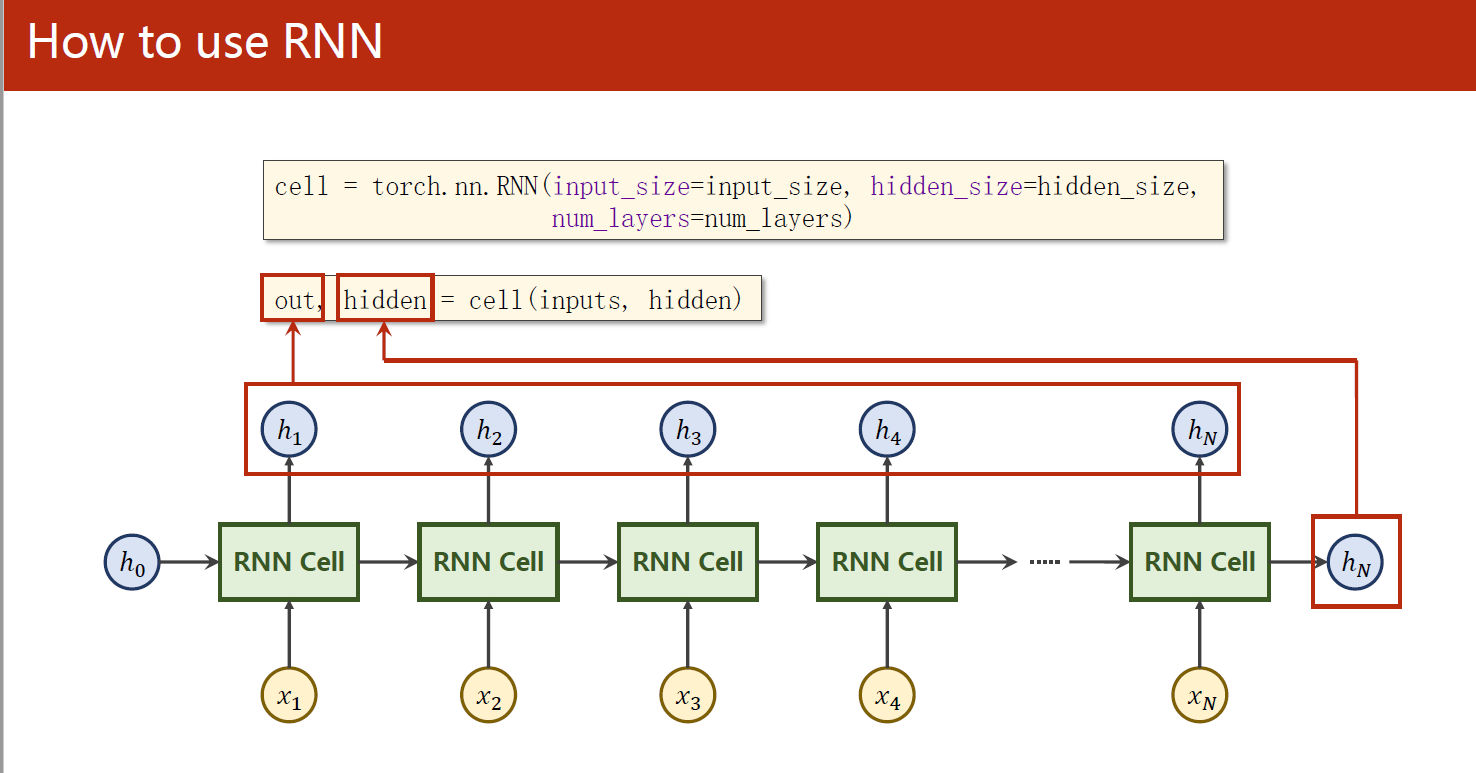
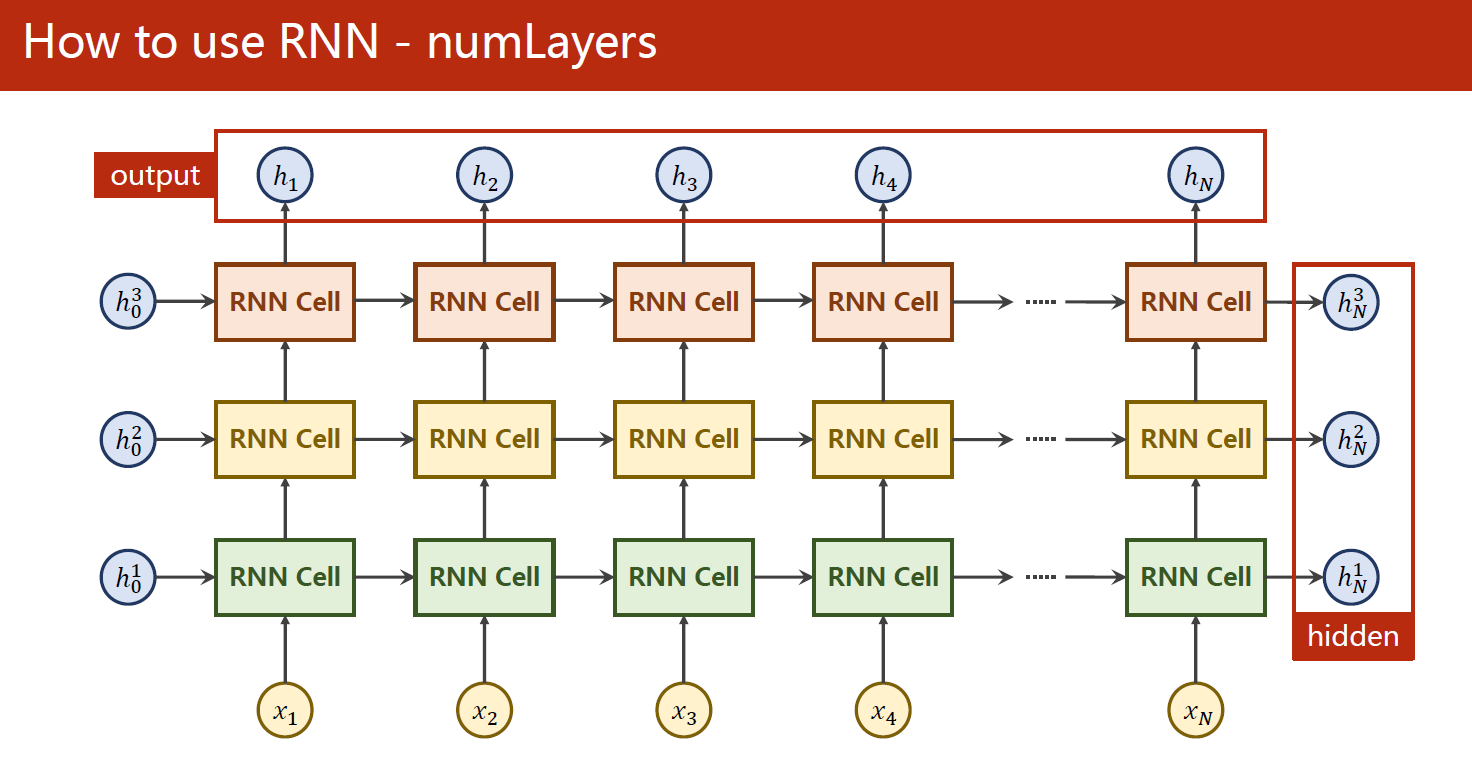
2.2 RNN

image-20230423130925511

image-20230423132517785

这段代码演示了如何使用PyTorch的RNN模块构建一个简单的RNN，并对一个简单的序列进行前向传递计算。

在这个例子中，我们首先构建了一个RNN对象，使用了输入维度为input_size、输出维度为hidden_size的隐藏层，并设置了RNN的层数num_layers为1（上图是num_layers为3的原理图，我们这里只使用了1层RNN）。接着，我们构造了一个大小为(seq_len, batch_size, input_size)的输入数据inputs，并将隐藏状态hidden初始化为全零张量，大小为(num_layers, batch_size, hidden_size)。

然后，我们将整个输入序列inputs输入到RNN中并得到输出output和最后一个时间步的隐藏状态hidden。在这个例子中，由于我们只有一个RNN层，因此hidden的大小与初始大小相同，仅仅是在第一维上添加了一个额外的维度。

最后，我们打印输出output和隐藏状态hidden的形状和值，以便了解RNN在整个序列上的输出情况。

具体来说，我们可以看到，整个输入序列的输出output是一个大小为(seq_len, batch_size, hidden_size) = (3, 1, 2)的张量。其中，第一维表示序列长度，第二维表示批次大小，第三维表示隐藏层输出的维度。而最后一个时间步的隐藏状态hidden是一个大小为(num_layers, batch_size, hidden_size) = (1, 1, 2)的张量。其中，第一维表示RNN的层数，第二维表示批次大小，第三维表示隐藏层输出的维度。

代码如下：

import torch

batch_size = 1
seq_len = 3
input_size = 4
hidden_size = 2
num_layers = 1  # RNN层数

# Construction of RNN
rnn = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)
# Wrapping the sequence into:(seqLen,batchSize,InputSize)
inputs = torch.randn(seq_len, batch_size, input_size)  # (3,1,4)
# Initializing the hidden to zero
hidden = torch.zeros(num_layers, batch_size, hidden_size)  # (1,1,2)

output, hidden = rnn(inputs, hidden)  # RNN内部包含了循环，故这里只需把整个序列输入即可

print('Output size:', output.shape)  # (seq_len, batch_size, hidden_size)
print('Output:', output)
print('Hidden size:', hidden.shape)  # (num_layers, batch_size, hidden_size)
print('Hidden:', hidden)

运行结果：

Output size: torch.Size([3, 1, 2])
Output: tensor([[[-0.9880, -0.8818]],

        [[ 0.6066,  0.9090]],

        [[-0.3108,  0.7957]]], grad_fn=<StackBackward0>)
Hidden size: torch.Size([1, 1, 2])
Hidden: tensor([[[-0.3108,  0.7957]]], grad_fn=<StackBackward0>)

可以看到，输出output是一个3维的张量，大小为(seq_len, batch_size, hidden_size) = (3, 1, 2)，在每个时间步的输出值都不同。最后一个时间步的隐藏状态hidden是一个3维的张量，大小为(num_layers, batch_size, hidden_size) = (1, 1, 2)，是整个序列的最后一个时间步的隐藏状态。

这个跟之前的RNNCell有什么不同呢？

前面的例子中使用了RNNCell，它只是RNN的一个单元，用于处理一个时间步的输入数据，需要在循环中手动处理时间步。而在这个例子中，我们使用了完整的RNN模型，它内部包含了循环结构，可以一次性处理整个序列的输入，从而避免了手动处理时间步的繁琐过程。

在上面的代码中，我们使用torch.nn.RNN构造了一个RNN模型，并将整个序列inputs输入到模型中，模型内部完成了所有的循环计算，并返回了整个序列的输出output和最后一个时间步的隐状态hidden。值得注意的是，模型中的hidden状态是在不同的时间步共享的，即当前时间步的隐状态hidden是由上一个时间步的输出和隐状态计算得到的，这与前面的RNNCell是类似的。但是，完整的RNN模型会自动完成时间步之间的循环，因此更加方便。

2.3 RNN参数：batch_first

在PyTorch中，RNN模型的输入通常是(seq_len, batch_size, input_size)这样的形式，即时间步序列排列在第一维，批量数据排列在第二维。但是，在某些情况下，我们可能更倾向于使用(batch_size, seq_len, input_size)的输入形式。为了满足这种需要，PyTorch提供了batch_first参数。

当batch_first=True时，输入和输出的形状就变成了(batch_size, seq_len, input_size)，这样就更符合一般的数据格式。在构造RNN模型时，只需将batch_first参数设置为True即可。

例如，对于一个RNN模型，当batch_first=False时，输入的形状为(seq_len, batch_size, input_size)，而当batch_first=True时，输入的形状为(batch_size, seq_len, input_size)。下面是一个示例：

import torch

batch_size = 1
seq_len = 3
input_size = 4
hidden_size = 2
num_layers = 1  # RNN层数

# Construction of RNN, batch_first=True
rnn = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers, batch_first=True)
# 仅这里做了更改 Wrapping the sequence into:(batchSize,seqLen,InputSize)
inputs = torch.randn(batch_size, seq_len, input_size)  # (1,3,4)
# Initializing the hidden to zero
hidden = torch.zeros(num_layers, batch_size, hidden_size)  # (1,1,2)

output, hidden = rnn(inputs, hidden)  # RNN内部包含了循环，故这里只需把整个序列输入即可

print('Output size:', output.shape)  # 输出维度发生变化(batch_size, seq_len, hidden_size)
print('Output:', output)
print('Hidden size:', hidden.shape)  # (num_layers, batch_size, hidden_size)
print('Hidden:', hidden)

Output size: torch.Size([1, 3, 2])
Output: tensor([[[ 0.6276, -0.1454],
         [ 0.0294,  0.3148],
         [-0.3239,  0.4692]]], grad_fn=<TransposeBackward1>)
Hidden size: torch.Size([1, 1, 2])
Hidden: tensor([[[-0.3239,  0.4692]]], grad_fn=<StackBackward0>)

在上面的例子中，我们构建了一个RNN模型，将batch_first参数设置为True，并将输入数据inputs的形状设置为(batch_size, seq_len, input_size)。通过这种方式，我们可以更方便地处理输入数据，而不用担心时间步和批量之间的顺序问题。

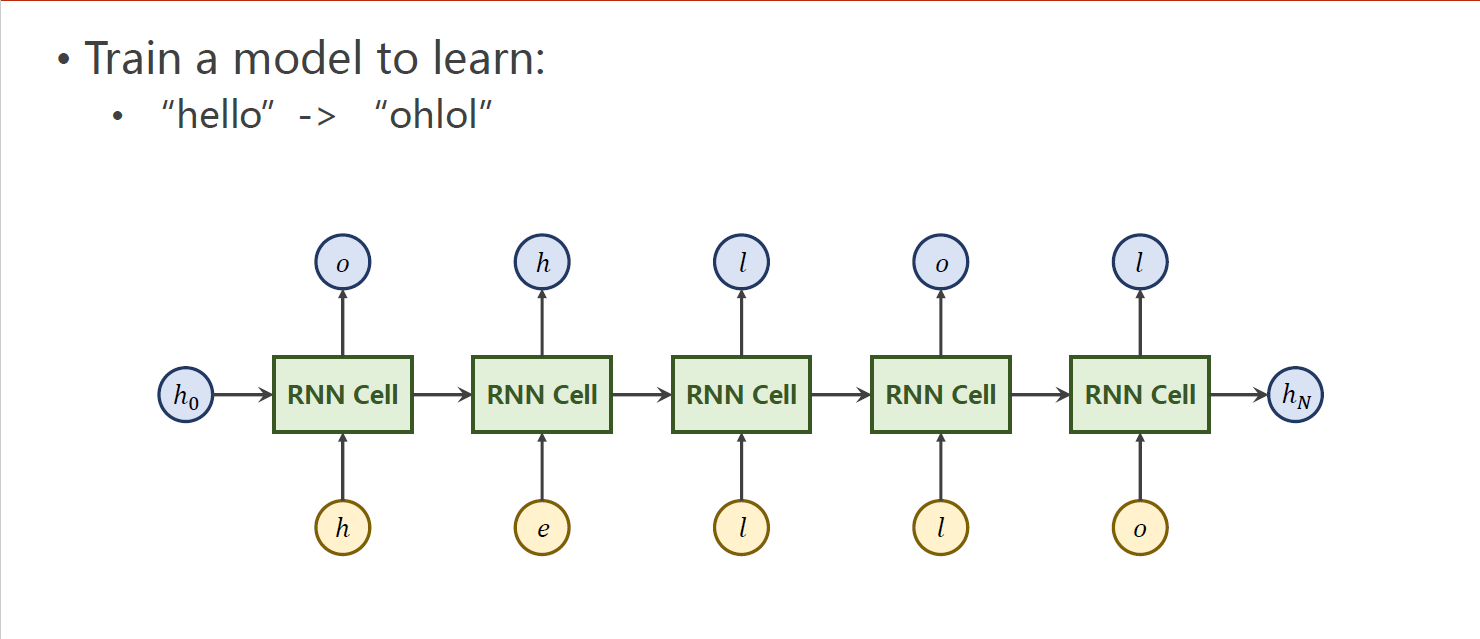
3 例子：序列变换把 “hello” --> “ohlol”

image-20230423133037919

3.1 使用RNNCell

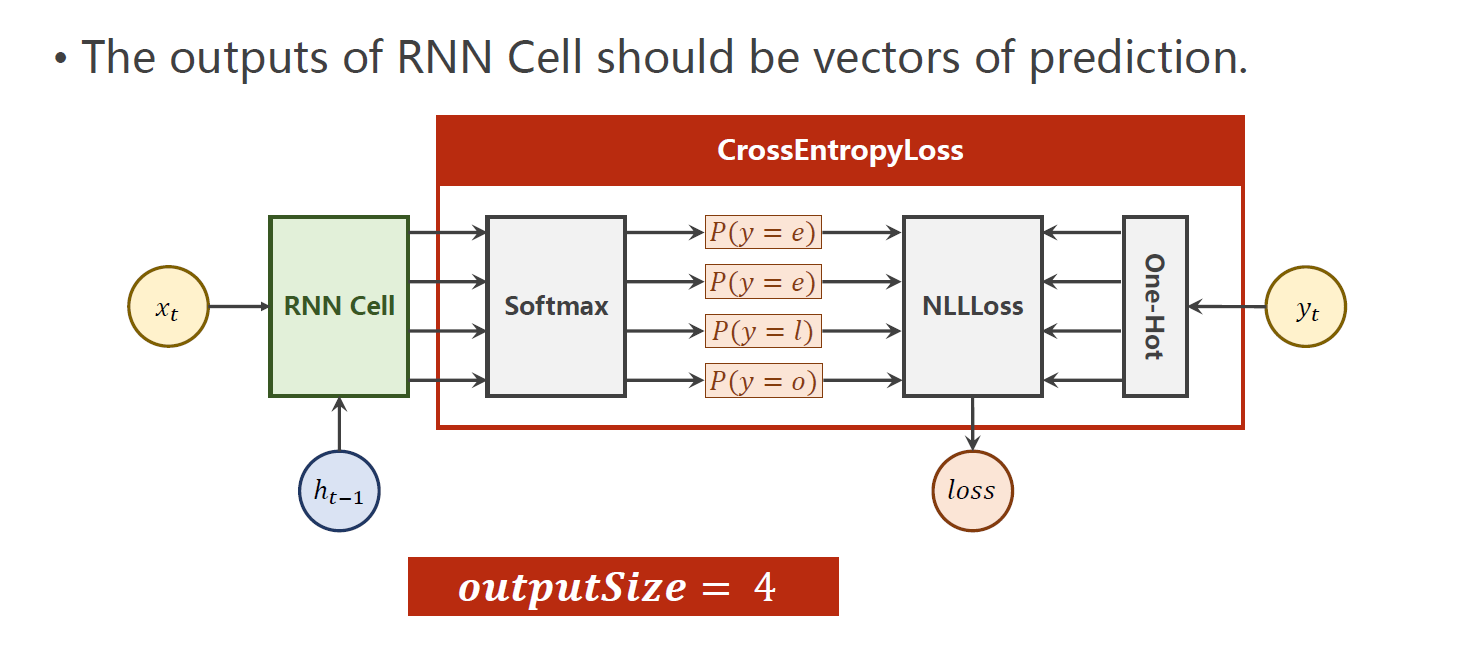
输入的独热编码示意图：

image-20230423133230333

输出示意图：

image-20230423133401053

这段代码是一个基于RNNCell的简单的字符级别的语言模型的训练过程。具体的训练过程如下：

  1. 定义了一个大小为input_size的输入向量，大小为hidden_size的隐藏向量和批次大小为batch_size的Model类，并且在这个类的初始化函数中，构建了一个RNNCell。
  2. 使用给定的索引，将输入序列转换为 one-hot 向量，并将输入序列和标签序列都进行维度变换，使其变为 (sequence_length, batch_size, input_size) 和 (sequence_length, 1)。
  3. 定义损失函数为交叉熵损失函数，优化器为 Adam。
  4. 在循环训练的过程中，每次输入一个字符，即按序列次序进行循环。每次训练前先将优化器的梯度清零，然后使用 net.init_hidden() 初始化隐藏层，并在循环中使用 net(input, hidden) 得到下一个时间步的隐藏状态。接着计算损失，进行反向传播，更新参数。每次循环中还会打印出预测的字符和当前损失。
  5. 循环训练15次，直到训练完成。
import torch

# 1、确定参数
input_size = 4
hidden_size = 4
batch_size = 1

# 2、准备数据
index2char = ['e', 'h', 'l', 'o']  #字典
x_data = [1, 0, 2, 2, 3]  #用字典中的索引（数字）表示来表示hello
y_data = [3, 1, 2, 3, 2]  #标签：ohlol

one_hot_lookup = [[1, 0, 0, 0],  # 用来将x_data转换为one-hot向量的参照表
                  [0, 1, 0, 0],
                  [0, 0, 1, 0],
                  [0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[x] for x in x_data]  #将x_data转换为one-hot向量
inputs = torch.Tensor(x_one_hot).view(-1, batch_size, input_size)  #(𝒔𝒆𝒒𝑳𝒆𝒏,𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒊𝒏𝒑𝒖𝒕𝑺𝒊𝒛𝒆)
labels = torch.LongTensor(y_data).view(-1, 1)  # (seqLen*batchSize,𝟏).计算交叉熵损失时标签不需要我们进行one-hot编码，其内部会自动进行处理


# 3、构建模型
class Model(torch.nn.Module):
    def __init__(self, input_size, hidden_size, batch_size):
        super(Model, self).__init__()
        self.batch_size = batch_size
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.rnncell = torch.nn.RNNCell(input_size=self.input_size, hidden_size=self.hidden_size)

    def forward(self, input, hidden):
        hidden = self.rnncell(input, hidden)
        return hidden

    def init_hidden(self):  #初始化隐藏层，需要batch_size
        return torch.zeros(self.batch_size, self.hidden_size)


net = Model(input_size, hidden_size, batch_size)

# 4、损失和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.1)  # Adam优化器

# 5、训练
for epoch in range(15):
    loss = 0
    optimizer.zero_grad()  #梯度清零
    hidden = net.init_hidden()  # 初始化隐藏层
    print('Predicted string:', end='')
    for input, label in zip(inputs, labels):  #每次输入一个字符，即按序列次序进行循环
        hidden = net(input, hidden)
        loss += criterion(hidden, label)  # 计算损失，不用item()，因为后面还要反向传播
        _, idx = hidden.max(dim=1)  # 选取最大值的索引
        print(index2char[idx.item()], end='')  # 打印预测的字符
    loss.backward()  # 反向传播
    optimizer.step()  # 更新参数
    print(', Epoch [%d/15] loss: %.4f' % (epoch + 1, loss.item()))

运行结果：

Predicted string:hehee, Epoch [1/15] loss: 8.2711
Predicted string:olhll, Epoch [2/15] loss: 6.2931
Predicted string:ollll, Epoch [3/15] loss: 5.3395
Predicted string:ollll, Epoch [4/15] loss: 4.7223
Predicted string:ohlll, Epoch [5/15] loss: 4.2614
Predicted string:ohlll, Epoch [6/15] loss: 3.9137
Predicted string:ohlol, Epoch [7/15] loss: 3.6579
Predicted string:ohlol, Epoch [8/15] loss: 3.4601
Predicted string:ohlol, Epoch [9/15] loss: 3.2896
Predicted string:ohlol, Epoch [10/15] loss: 3.1306
Predicted string:ohlol, Epoch [11/15] loss: 2.9806
Predicted string:ohlol, Epoch [12/15] loss: 2.8476
Predicted string:ohlol, Epoch [13/15] loss: 2.7450
Predicted string:ohlol, Epoch [14/15] loss: 2.6792
Predicted string:ohlol, Epoch [15/15] loss: 2.6347

3.2 使用RNN

在代码中，首先定义了一个RNN模型的类Model，继承自torch.nn.Module。这个模型接受一个input_size表示输入的向量维度，一个hidden_size表示隐藏层的向量维度，一个batch_size表示每批次输入数据的样本数量，以及一个可选的num_layers表示RNN的层数。

在这个类中，定义了一个RNN层self.rnn，输入为input_size和hidden_size，并指定层数为num_layers。在前向传播过程中，将输入数据input和一个全零张量hidden输入到RNN层中，然后将输出张量out从三维张量转换为二维张量，并返回输出张量。

在训练时，首先将优化器的梯度清零，然后将输入数据inputs送入模型中得到输出outputs。将输出outputs和标签labels输入到交叉熵损失函数中计算损失，然后通过反向传播计算梯度，并调用优化器的step方法更新模型参数。

最后，将输出outputs中每个时间步的预测结果取出来，转换为对应的字符，打印出来。同时，输出当前的损失和训练轮数。

import torch

# 1、确定参数
seq_len = 5
input_size = 4
hidden_size = 4
batch_size = 1

# 2、准备数据
index2char = ['e', 'h', 'l', 'o']  #字典
x_data = [1, 0, 2, 2, 3]  #用字典中的索引（数字）表示来表示hello
y_data = [3, 1, 2, 3, 2]  #标签：ohlol

one_hot_lookup = [[1, 0, 0, 0],  # 用来将x_data转换为one-hot向量的参照表
                  [0, 1, 0, 0],
                  [0, 0, 1, 0],
                  [0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[x] for x in x_data]  #将x_data转换为one-hot向量
inputs = torch.Tensor(x_one_hot).view(seq_len, batch_size,
                                      input_size)  #(𝒔𝒆𝒒𝑳𝒆𝒏,𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒊𝒏𝒑𝒖𝒕𝑺𝒊𝒛𝒆)
labels = torch.LongTensor(y_data)


# 3、构建模型
class Model(torch.nn.Module):
    def __init__(self, input_size, hidden_size, batch_size, num_layers=1):
        super(Model, self).__init__()
        self.num_layers = num_layers
        self.batch_size = batch_size
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.rnn = torch.nn.RNN(input_size=self.input_size, hidden_size=self.hidden_size, num_layers=num_layers)

    def forward(self, input):
        hidden = torch.zeros(self.num_layers, self.batch_size, self.hidden_size)
        out, _ = self.rnn(input, hidden)  # out: tensor of shape (seq_len, batch, hidden_size)
        return out.view(-1, self.hidden_size)  # 将输出的三维张量转换为二维张量,(𝒔𝒆𝒒𝑳𝒆𝒏×𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒉𝒊𝒅𝒅𝒆𝒏𝑺𝒊𝒛𝒆)

    def init_hidden(self):  #初始化隐藏层，需要batch_size
        return torch.zeros(self.batch_size, self.hidden_size)


net = Model(input_size, hidden_size, batch_size, num_layers)

# 4、损失和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)  # Adam优化器

# 5、训练
for epoch in range(15):
    optimizer.zero_grad()
    outputs = net(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

    _, idx = outputs.max(dim=1)
    idx = idx.data.numpy()
    print('Predicted string: ', ''.join([index2char[x] for x in idx]), end='')
    print(', Epoch [%d/15] loss: %.4f' % (epoch + 1, loss.item()))

运行结果：

Predicted string:  hhhhh, Epoch [1/15] loss: 1.4325
Predicted string:  hhhhh, Epoch [2/15] loss: 1.2532
Predicted string:  ohhoh, Epoch [3/15] loss: 1.1057
Predicted string:  ohlol, Epoch [4/15] loss: 0.9970
Predicted string:  ohlol, Epoch [5/15] loss: 0.9208
Predicted string:  oolol, Epoch [6/15] loss: 0.8669
Predicted string:  oolol, Epoch [7/15] loss: 0.8250
Predicted string:  oolol, Epoch [8/15] loss: 0.7863
Predicted string:  oolol, Epoch [9/15] loss: 0.7453
Predicted string:  oolol, Epoch [10/15] loss: 0.7024
Predicted string:  oolol, Epoch [11/15] loss: 0.6625
Predicted string:  oolol, Epoch [12/15] loss: 0.6291
Predicted string:  ohlol, Epoch [13/15] loss: 0.6026
Predicted string:  ohlol, Epoch [14/15] loss: 0.5812
Predicted string:  ohlol, Epoch [15/15] loss: 0.5630

在这段代码中，labels不需要进行.view(-1, 1)处理的原因是因为它是一个一维的LongTensor张量，形状为(seq_len,)。在 PyTorch 的交叉熵损失函数 torch.nn.CrossEntropyLoss() 中，标签需要被表示成一维的长整型张量。这是因为交叉熵损失函数在内部将标签进行了one-hot编码，并使用这些编码来计算预测值和标签之间的损失。

在这段代码中，由于 labels 是一个一维张量，因此无需进行形状变换。当然，如果你将 labels 转换为 (seq_len, 1) 的形状也可以，但是在这种情况下，torch.nn.CrossEntropyLoss() 会自动将其转换回一维张量，所以不必进行此操作。

3.3 使用embedding and linear layer

在使用独热编码作为RNN输入时，有以下几个缺点：

  1. 维度灾难：对于大规模的数据集和多类分类问题，独热编码会导致输入数据维度极度膨胀，从而导致模型参数变得非常庞大，训练和推理时间变慢。
  2. 数据稀疏性：独热编码会使得大部分输入都是0，因为只有一个位置是1，这导致输入数据非常稀疏，浪费了大量的存储空间和计算资源。
  3. 无法表达序列信息：在RNN中，序列的顺序很重要，但是独热编码无法表达序列信息，只能表达每个输入在类别上的差异。因此，在处理序列数据时，独热编码可能无法捕捉到序列中的模式和规律。
  4. 无法处理未知类别：独热编码需要预先知道类别的数量，如果遇到新的类别，需要重新扩展编码向量，这会带来额外的开销和复杂度。

因此，在某些情况下，可以考虑使用其他的编码方式来解决这些问题，例如使用嵌入（embedding）向量来表示输入数据，或者使用特征哈希（feature hashing）等技术来降低维度。

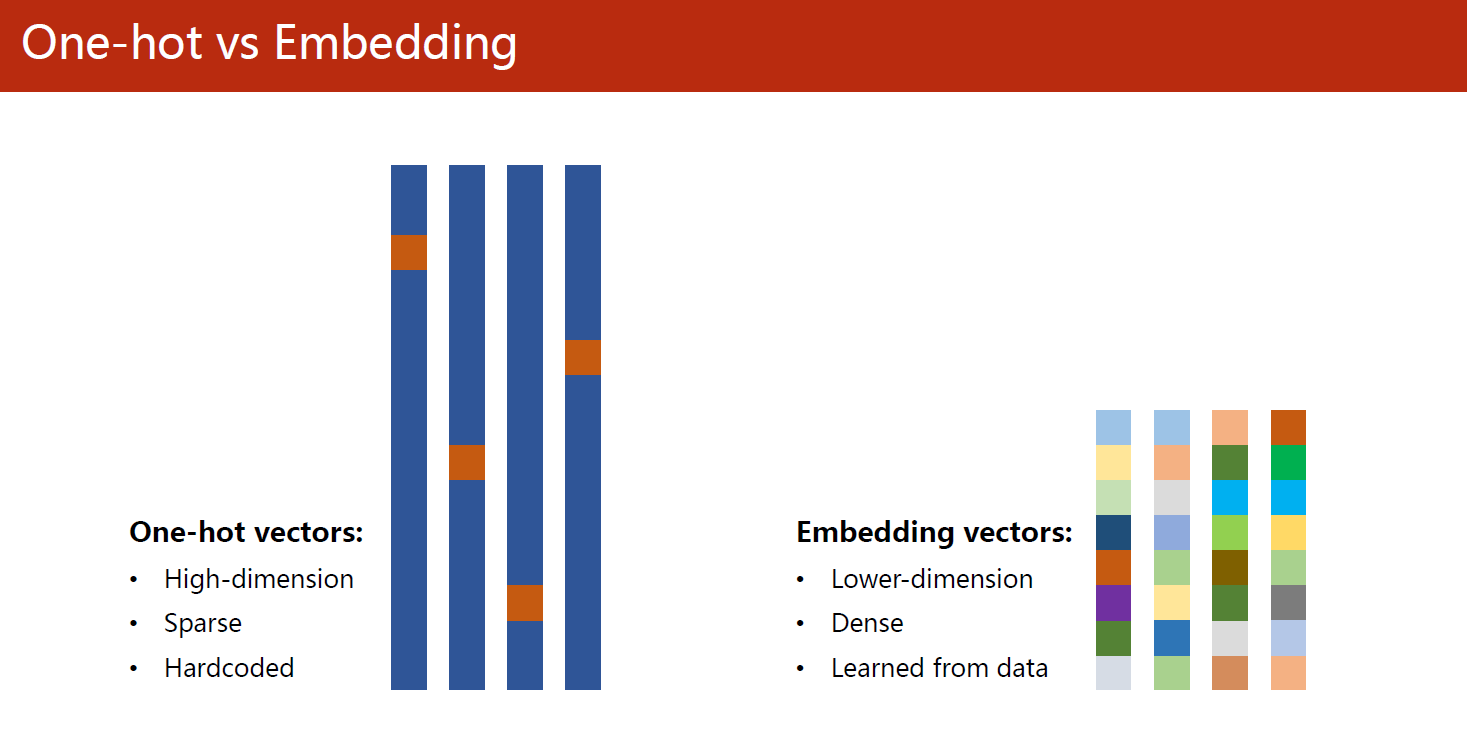
image-20230423135726064

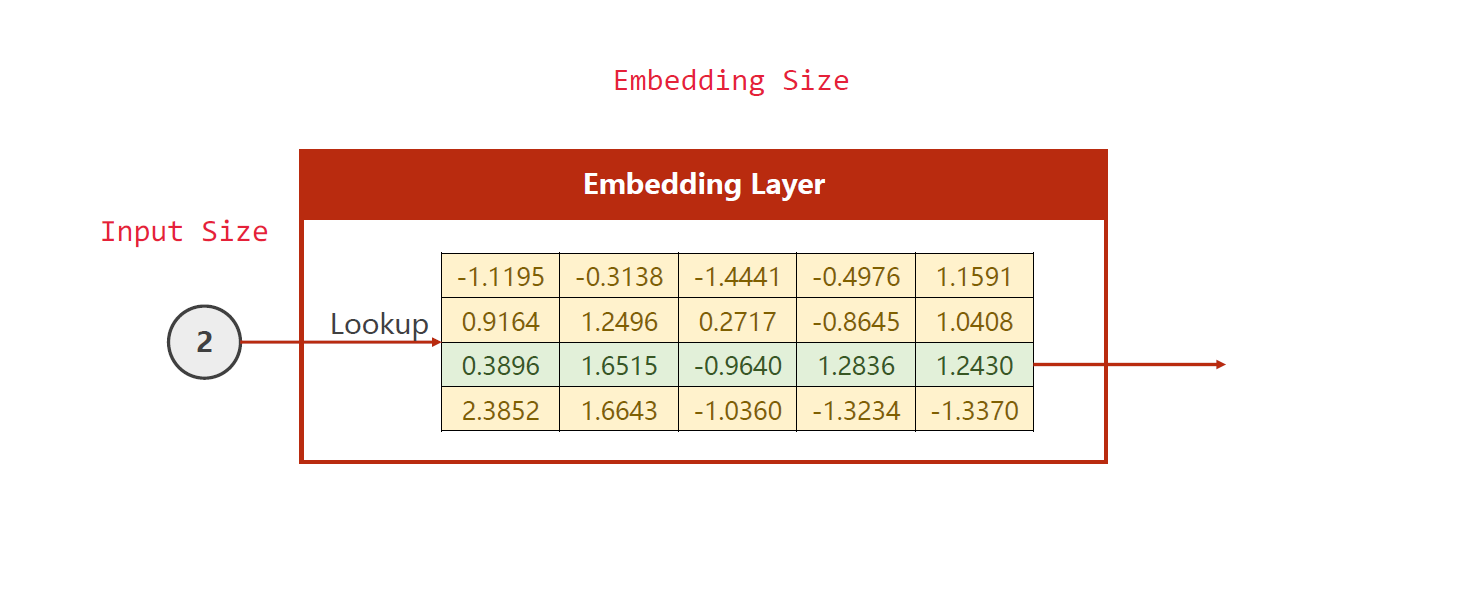
嵌入（embedding）向量

嵌入（embedding）向量是一种将离散型数据（如词语、用户ID等）映射到连续型向量空间中的技术，常用于自然语言处理、推荐系统等领域。

嵌入向量的原理是利用神经网络中的一层或多层进行映射。假设有n个离散化的元素，每个元素用一个唯一的整数进行编码。嵌入层的输入是这些编码，输出是每个编码对应的k维嵌入向量，通常k的值会远小于n，因此将数据从一个大的高维空间压缩到一个较小的低维空间。

在嵌入层中，每个元素的编码都被映射为一个固定长度的向量，且不同元素的向量之间可以计算相似度，这个相似度在一定程度上反映了它们在原始数据中的关系。例如，在自然语言处理中，相似的单词（如“cat”和“dog”）在嵌入空间中的向量会更加接近，因为它们在语义上有一定的相关性。

image-20230423140105849

嵌入向量在许多应用中被广泛使用，例如语言模型、情感分析、推荐系统等。在自然语言处理中，通过使用嵌入向量可以将文本转换为数字，从而方便机器学习算法处理。同时，由于嵌入向量的低维度表示，计算速度较快，可以处理大规模数据集。

image-20230423140241004

相关函数

image-20230423141828128

image-20230423141848208

image-20230423141912482

代码

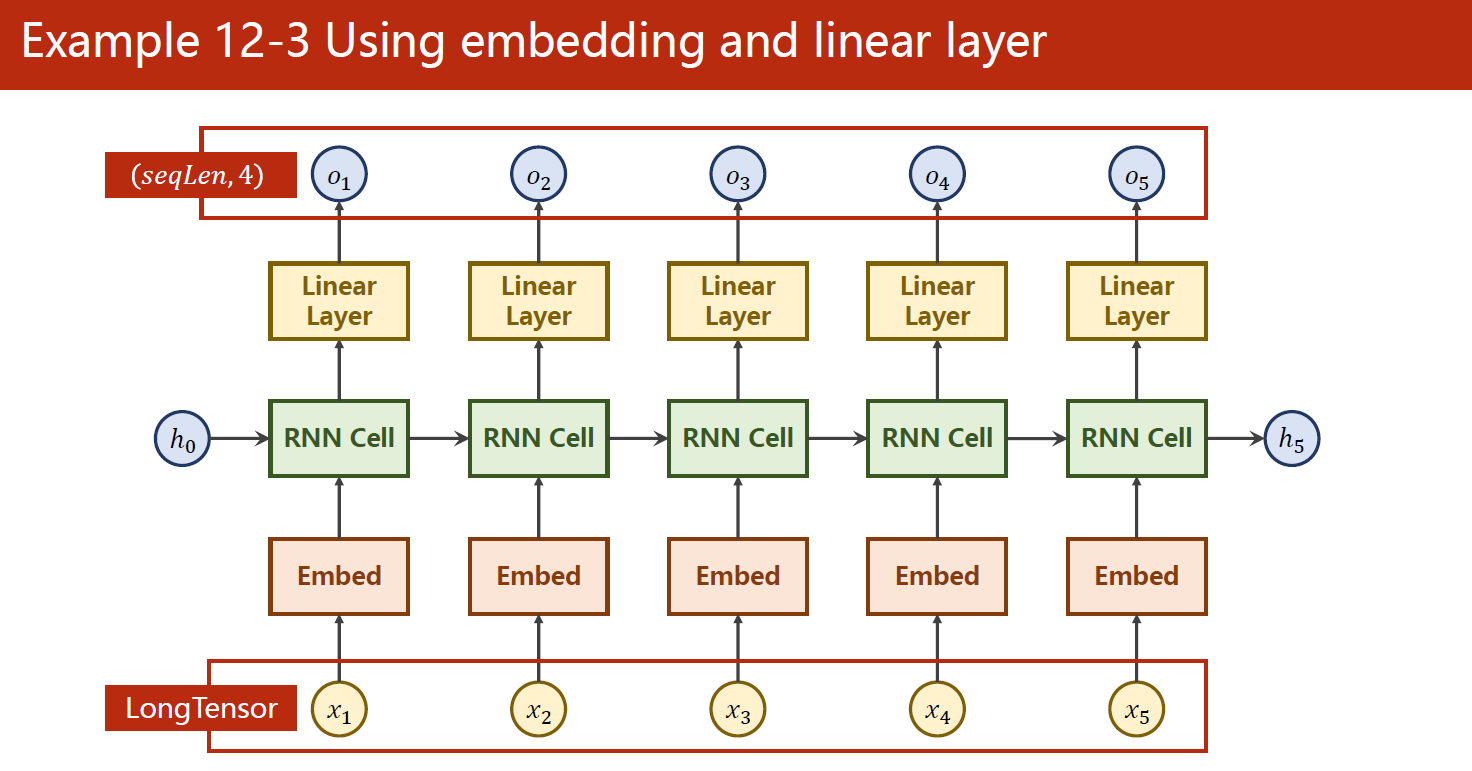
这段代码是一个基于RNN的字符级别的语言模型，用于预测给定输入字符序列的下一个字符。下面是对代码的解释和说明：

  1. 在确定参数的部分，定义了RNN的输入和输出大小、隐藏状态的维度、Embedding向量的大小、RNN层数等参数，这些参数将会在模型的构建中使用。
  2. 在准备数据的部分，定义了一个字典index2char用于将数字索引映射到字符，输入数据x_data是一段英文字符串"hello"，并将其转换为数字索引的形式。
  3. 在构建模型的部分，使用了PyTorch中的Embedding层将输入字符的数字索引转换为固定长度的向量表示，该向量表示将在RNN中传递。使用RNN层将Embedding向量作为输入，计算RNN的输出。最后，通过一个全连接层fc将RNN的输出映射到每个字符的概率分布。在这个模型中，全连接层的作用是对RNN的输出做一个线性变换，从而将输出的维度从隐藏状态的维度变为每个字符的数量。
  4. 在定义损失函数和优化器的部分，使用了交叉熵损失函数作为模型的损失函数，Adam优化器来更新模型的参数。
  5. 在训练模型的部分，使用一个简单的循环进行模型的训练，每次训练输出当前训练次数和损失值，并打印出模型预测的字符串。在这个过程中，每个字符的Embedding向量会随着训练不断调整，最终使模型能够对字符序列做出准确的预测。
import torch

# 1、确定参数
num_class = 4
input_size = 4
hidden_size = 8
embedding_size = 10
num_layers = 2
batch_size = 1
seq_len = 5

# 2、准备数据
index2char = ['e', 'h', 'l', 'o']  #字典
x_data = [[1, 0, 2, 2, 3]]  # (batch_size, seq_len) 用字典中的索引（数字）表示来表示hello
y_data = [3, 1, 2, 3, 2]  #  (batch_size * seq_len) 标签：ohlol

inputs = torch.LongTensor(x_data)  # (batch_size, seq_len)
labels = torch.LongTensor(y_data)  # (batch_size * seq_len)


# 3、构建模型
class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.emb = torch.nn.Embedding(num_class, embedding_size)
        self.rnn = torch.nn.RNN(input_size=embedding_size, hidden_size=hidden_size, num_layers=num_layers,
                                batch_first=True)
        self.fc = torch.nn.Linear(hidden_size, num_class)

    def forward(self, x):
        hidden = torch.zeros(num_layers, x.size(0), hidden_size)  # (num_layers, batch_size, hidden_size)
        x = self.emb(x)  # 返回(batch_size, seq_len, embedding_size)
        x, _ = self.rnn(x, hidden)  # 返回(batch_size, seq_len, hidden_size)
        x = self.fc(x)  # 返回(batch_size, seq_len, num_class)
        return x.view(-1, num_class)  # (batch_size * seq_len, num_class)


net = Model()

# 4、损失和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)  # Adam优化器

# 5、训练
for epoch in range(15):
    optimizer.zero_grad()
    outputs = net(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

    _, idx = outputs.max(dim=1)
    idx = idx.data.numpy()
    print('Predicted string: ', ''.join([index2char[x] for x in idx]), end='')
    print(', Epoch [%d/15] loss: %.4f' % (epoch + 1, loss.item()))

运行结果：

Predicted string:  eeeee, Epoch [1/15] loss: 1.5407
Predicted string:  oolol, Epoch [2/15] loss: 1.1158
Predicted string:  oolol, Epoch [3/15] loss: 0.9047
Predicted string:  ohlol, Epoch [4/15] loss: 0.7391
Predicted string:  lhlol, Epoch [5/15] loss: 0.6006
Predicted string:  ohlol, Epoch [6/15] loss: 0.4833
Predicted string:  ohlol, Epoch [7/15] loss: 0.3581
Predicted string:  ohlol, Epoch [8/15] loss: 0.2540
Predicted string:  ohlol, Epoch [9/15] loss: 0.1921
Predicted string:  ohlol, Epoch [10/15] loss: 0.1351
Predicted string:  ohlol, Epoch [11/15] loss: 0.0972
Predicted string:  ohlol, Epoch [12/15] loss: 0.0752
Predicted string:  ohlol, Epoch [13/15] loss: 0.0594
Predicted string:  ohlol, Epoch [14/15] loss: 0.0465
Predicted string:  ohlol, Epoch [15/15] loss: 0.0363

4 LSTM和GRU

上面 RNN 模型也存在一些局限性：

  1. 梯度消失和梯度爆炸问题：当序列非常长时，梯度可能会逐渐消失或爆炸，导致网络无法学习长序列的依赖关系。

  2. 只能学习固定长度的序列：由于 RNN 的输入和输出都是固定长度的，因此模型只能学习固定长度的序列。

  3. 处理不同时间步的输入时存在数据对齐问题：在训练 RNN 时，需要将不同长度的序列对齐到相同的长度，这通常需要一些预处理和后处理，而且可能会导致信息丢失或噪声引入。

  4. 无法很好地处理长期依赖关系：尽管 RNN 可以学习一定的序列依赖性，但是当序列的时间跨度很大时，RNN 可能会出现长期依赖问题。此外，由于 RNN 的循环结构，每个时间步的输出都依赖于前一时间步的状态，因此模型可能会受到某些时间步的信息干扰。

有几种方法可以尝试解决RNN模型的一些局限性：

  1. 使用更高级别的模型：可以使用一些更先进的模型，如LSTM（长短期记忆网络）和GRU（门控循环单元）等，这些模型在一定程度上解决了RNN模型存在的一些问题。
  2. 添加注意力机制：注意力机制可以帮助模型在输入序列中关注不同的部分，并对重要的部分进行加权，从而提高模型的准确性。
  3. 使用更多的数据：增加数据量可以帮助模型更好地学习输入序列的规律，从而提高模型的准确性。
  4. 对数据进行预处理：对输入数据进行预处理，如归一化、降噪、平滑等，可以提高模型的鲁棒性和准确性。
  5. 结合其他技术：可以结合其他技术来解决模型存在的问题，如集成学习、正则化、Dropout等。

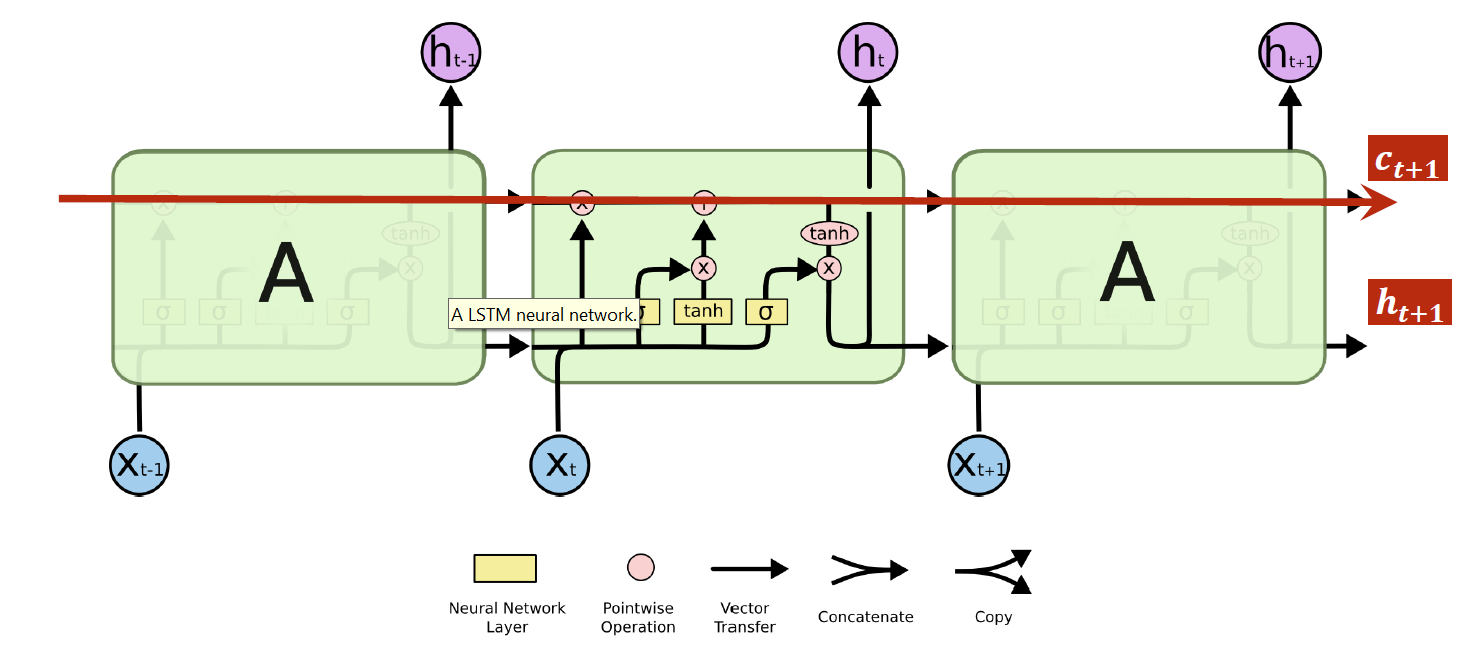
LSTM（Long Short-Term Memory，长短期记忆网络）和GRU（Gated Recurrent Unit，门控循环单元）是常用的循环神经网络（RNN）的变种，相比于传统的RNN，它们能够更好地处理长序列数据，解决了传统RNN中的梯度消失和梯度爆炸问题。

LSTM的主要思想是引入一个称为“细胞状态”（cell state）的记忆单元，以及三个门（输入门、遗忘门和输出门）来控制对细胞状态的访问和更新。其中，输入门决定了新的输入如何影响细胞状态，遗忘门决定了何时忘记旧的细胞状态，输出门决定了输出什么样的信息。LSTM的结构相对复杂，需要较高的计算资源和训练时间。

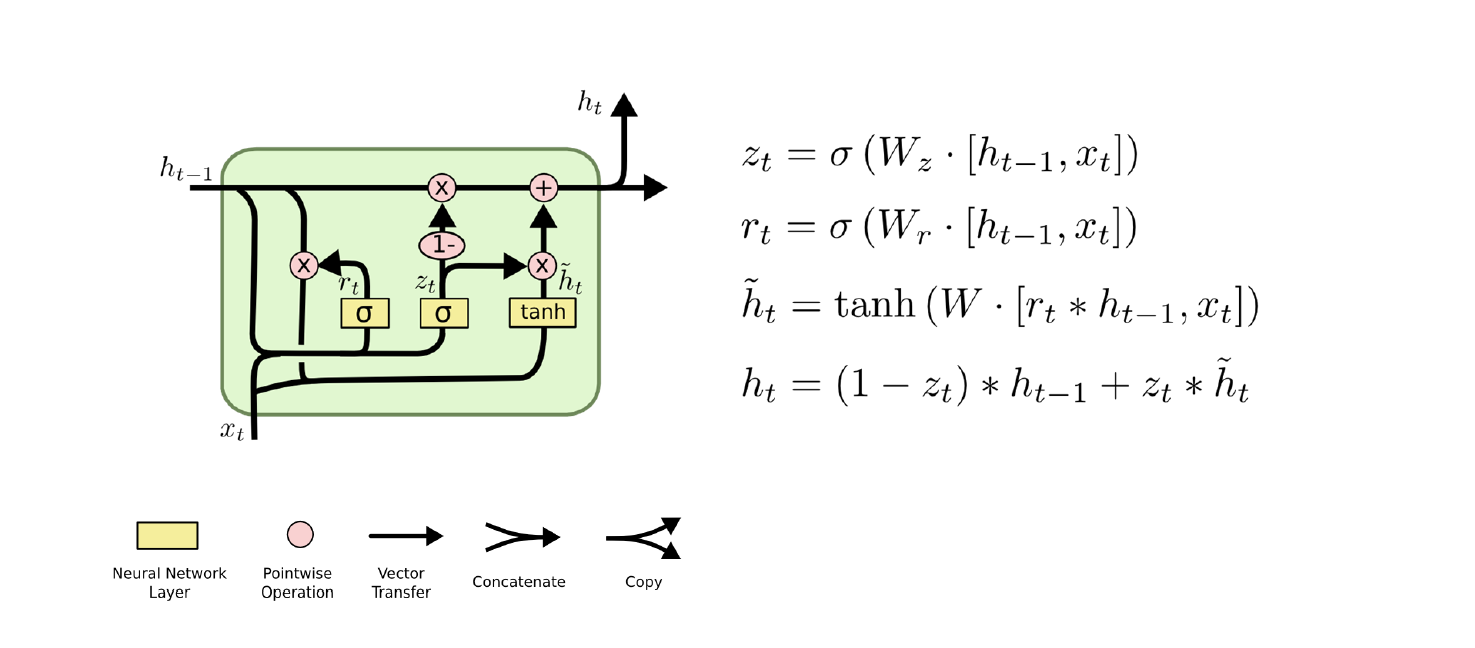
GRU是由Cho等人于2014年提出的一种轻量级的门控循环单元，它只包含两个门（更新门和重置门），通过控制输入和历史状态的权重来控制信息流动。GRU的结构比LSTM简单，计算量也相对较小，同时在处理长序列数据时也具有不错的效果。

总的来说，LSTM和GRU是目前在循环神经网络领域中表现优异的模型，但具体选择哪种模型需要根据具体的任务和数据集来决定。

image-20230423142703707

image-20230423142740832

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
水印 截屏攻击 matlab,数字水印常见攻击类型汇总，噪声，缩放，旋转，剪切（附matlab代码）...
实验三：熟悉常用的HBase操作
（附源码）计算机毕业设计SSM基于的二手车商城
初识git · 有关模型
中国疫情发展趋势分析预测（python实现）
Javaweb学习之JavaScript输出与字符串（二）
OpenCV中Mat类型与C#中Bitmap类型的转换
群晖ssh登录并开启root用户登录功能
知乎广告怎么做？知乎种树推广怎么收费？
详解Vmware+Linux+Oracle10g rac全过程
;