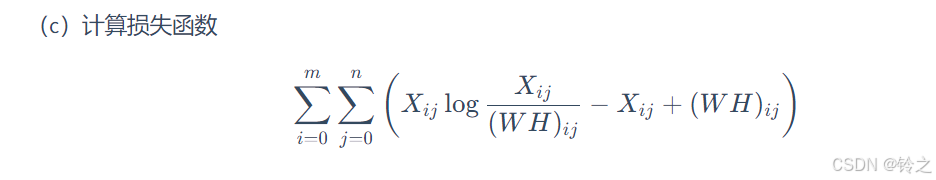第17章潜在语义分析：奇异值分解、非负矩阵分解及课后习题

1.单词向量空间模型通过单词的向量表示文本的语义内容。以单词-文本矩阵 $X$ 为输入，其中每一行对应一个单词，每一列对应一个文本，每一个元素表示单词在文本中的频数或权值（如TF-IDF）
$\left[ \begin{array} { c c c c } { x _ { 11 } } & { x _ { 12 } } & { \cdots } & { x _ { 1 n } } \\ { x _ { 21 } } & { x _ { 22 } } & { \cdots } & { x _ { 2 n } } \\ { \vdots } & { \vdots } & { } & { \vdots } \\ { x _ { m 1 } } & { x _ { m 2 } } & { \cdots } & { x _ { m n } } \end{array} \right]$
单词向量空间模型认为，这个矩阵的每一列向量是单词向量，表示一个文本，两个单词向量的内积或标准化内积表示文本之间的语义相似度。

TF-IDF 是词频-逆文档频率（Term Frequency-Inverse Document Frequency），这个值越大，表示词语 $t_i$ 在文档 $d_j$ 中越重要。它结合了词语在单个文档中的频率和词语在整个文档集中出现的稀有程度，能够有效地衡量词语的重要性。公式如下：

$\text{TF-IDF}_{ij} = \frac{tf_{ij}}{tf_{j}} \times \log \left( \frac{df}{df_i} \right)$

词频部分：
$\frac{tf_{ij}}{tf_{j}}$
- $tf_{ij}$ ：词语 $t_i$ 在文档 $d_j$ 中出现的次数。
- $tf_{j}$ ：文档 $d_j$ 中所有词语出现的总次数。
这个部分计算的是词语 $t_i$ 在文档 $d_j$ 中的相对词频（Term Frequency, TF），即词语在文档中出现的频率。
逆文档频率部分：
$\log \left( \frac{df}{df_i} \right)$
- $df$ ：文档集中所有文档的总数。
- $df_i$ ：包含词语 $t_i$ 的文档数。
这个部分计算的是词语 $t_i$ 的逆文档频率（Inverse Document Frequency, IDF）。当词语 $t_i$ 出现在较少的文档中时，IDF值较高，表示该词语对区分文档的重要性较大。反之，如果词语 $t_i$ 出现在许多文档中，IDF值较低，表示该词语对区分文档的重要性较小。

2.话题向量空间模型通过话题的向量表示文本的语义内容。假设有话题文本矩阵 $\left[ \begin{array} { c c c c } { y _ { 11 } } & { y _ { 12 } } & { \cdots } & { y _ { 1 n } } \\ { y _ { 21 } } & { y _ { 22 } } & { \cdots } & { y _ { 2 n } } \\ { \vdots } & { \vdots } & { } & { \vdots } \\ { y _ { k 1 } } & { y _ { k 2 } } & { \cdots } & { y _ { k n } } \end{array} \right]$
其中每一行对应一个话题，每一列对应一个文本，每一个元素表示话题在文本中的权值。话题向量空间模型认为，这个矩阵的每一列向量是话题向量，表示一个文本，两个话题向量的内积或标准化内积表示文本之间的语义相似度。假设有单词话题矩阵 $T$
$\left[ \begin{array} { c c c c } { t _ { 11 } } & { t _ { 12 } } & { \cdots } & { t _ { 1 k } } \\ { t _ { 21 } } & { t _ { 22 } } & { \cdots } & { t _ { 2 k } } \\ { \vdots } & { \vdots } & { } & { \vdots } \\ { t _ { m 1 } } & { t _ { m 2 } } & { \cdots } & { t _ { m k } } \end{array} \right]$
其中每一行对应一个单词，每一列对应一个话题，每一个元素表示单词在话题中的权值。

给定一个单词文本矩阵 $X$
$\left[ \begin{array} { c c c c } { x _ { 11 } } & { x _ { 12 } } & { \cdots } & { x _ { 1 n } } \\ { x _ { 21 } } & { x _ { 22 } } & { \cdots } & { x _ { 2 n } } \\ { \vdots } & { \vdots } & { } & { \vdots } \\ { x _ { m 1 } } & { x _ { m 2 } } & { \cdots } & { x _ { m n } } \end{array} \right]$

潜在语义分析的目标是，找到合适的单词-话题矩阵 $T$ 与话题-文本矩阵 $Y$ ，将单词-文本矩阵 $X$ 近似的表示为 $T$ 与 $Y$ 的乘积形式。
$\approx T Y$

等价地，潜在语义分析将文本在单词向量空间的表示X通过线性变换 $T$ 转换为话题向量空间中的表示 $Y$ 。

潜在语义分析的关键是对单词-文本矩阵进行以上的矩阵因子分解（话题分析）

3.潜在语义分析的算法是奇异值分解。通过对单词文本矩阵进行截断奇异值分解，得到
$\approx U _ { k } \Sigma _ { k } V _ { k } ^ { T } = U _ { k } ( \Sigma _ { k } V _ { k } ^ { T } )$

矩阵 $U_k$ 表示话题空间，矩阵 $\Sigma _ { k } V _ { k } ^ { T } )$ 是文本在话题空间的表示。

4.非负矩阵分解也可以用于话题分析。非负矩阵分解将非负的单词文本矩阵近似分解成两个非负矩阵 $W$ 和 $H$ 的乘积，得到
$\approx W H$

矩阵 $W$ 表示话题空间，矩阵 $H$ 是文本在话题空间的表示。

非负矩阵分解可以表为以下的最优化问题：
$\left. \begin{array} { l } { \operatorname { min } _ { W , H } \| X - W H \| ^ { 2 } } \\ { \text { s.t. } W , H \geq 0 } \end{array} \right.$
非负矩阵分解的算法是迭代算法。乘法更新规则的迭代算法，交替地对 $W$ 和 $H$ 进行更新。本质是梯度下降法，通过定义特殊的步长和非负的初始值，保证迭代过程及结果的矩阵 $W$ 和 $H$ 均为非负。

非负矩阵分解（NMF）

NMF 是一种矩阵分解技术，用于将一个非负矩阵 $X$ 分解为两个非负矩阵 $W$ 和 $H$ 的乘积，即：

$\approx W \cdot H$

其中：

$X$ 是原始的非负矩阵，维度为 $\times n$ 。
$W$ 是左因子矩阵，维度为 $\times k$ 。
$H$ 是右因子矩阵，维度为 $\times n$ 。
$k$ 是分解的潜在特征的数量，也就是我们选择的维度。

这种分解方法在文本挖掘、图像处理和推荐系统中广泛应用。

import numpy as np

# 保留两位小数，不使用科学计数法
np.set_printoptions(precision=2, suppress=True)


def inverse_transform(W, H):
    # 重构
    return W.dot(H)


def loss(X, X_):
    #计算重构误差
    return ((X - X_) * (X - X_)).sum()


# 基于平方损失的算法 17.1
class MyNMF:
    def fit(self, X, k, t):
        m, n = X.shape

        W = np.random.rand(m, k)
        W = W / W.sum(axis=0)

        H = np.random.rand(k, n)

        i = 1
        while i < t:

            W = W * X.dot(H.T) / W.dot(H).dot(H.T)

            H = H * (W.T).dot(X) / (W.T).dot(W).dot(H)

            i += 1

        return W, H

X = [[2, 0, 0, 0], [0, 2, 0, 0], [0, 0, 1, 0], [0, 0, 2, 3], [0, 0, 0, 1],
     [1, 2, 2, 1]]
X = np.asarray(X)
model = MyNMF()
W, H = model.fit(X, 3, 200)
print('W:\n', W)
print('H:\n', H)

# 重构
X_ = inverse_transform(W, H)
print('X:\n', X)
print('X_:\n', X_)
print('重构损失：', loss(X, X_))

W:
 [[0.   0.39 0.  ]
 [0.   0.78 0.  ]
 [0.   0.   0.4 ]
 [1.44 0.   0.75]
 [0.49 0.   0.  ]
 [0.46 0.97 0.78]]
H:
 [[0.   0.   0.08 2.05]
 [1.03 2.06 0.01 0.01]
 [0.01 0.01 2.5  0.07]]
X:
 [[2 0 0 0]
 [0 2 0 0]
 [0 0 1 0]
 [0 0 2 3]
 [0 0 0 1]
 [1 2 2 1]]
X_:
 [[0.4  0.8  0.01 0.  ]
 [0.8  1.6  0.01 0.01]
 [0.   0.   1.   0.03]
 [0.   0.01 2.   3.  ]
 [0.   0.   0.04 1.  ]
 [1.   2.   2.   1.  ]]
重构损失： 4.002696167437877

# 使用sklearn
from sklearn.decomposition import NMF

model = NMF(n_components=3, init='random', random_state=0)
W = model.fit_transform(X)
H = model.components_
print('W:\n', W)
print('H:\n', H)

# 重构
X_ = inverse_transform(W, H)
print('X:\n', X)
print('X_:\n', X_)
print('重构损失：', loss(X, X_))

W:
 [[0.   0.54 0.  ]
 [0.   1.08 0.  ]
 [0.7  0.   0.  ]
 [1.4  0.   1.97]
 [0.   0.   0.66]
 [1.4  1.35 0.66]]
H:
 [[0.   0.   1.43 0.  ]
 [0.74 1.49 0.   0.  ]
 [0.   0.   0.   1.52]]
X:
 [[2 0 0 0]
 [0 2 0 0]
 [0 0 1 0]
 [0 0 2 3]
 [0 0 0 1]
 [1 2 2 1]]
X_:
 [[0.4 0.8 0.  0. ]
 [0.8 1.6 0.  0. ]
 [0.  0.  1.  0. ]
 [0.  0.  2.  3. ]
 [0.  0.  0.  1. ]
 [1.  2.  2.  1. ]]
重构损失： 4.000001672582457

习题17.1

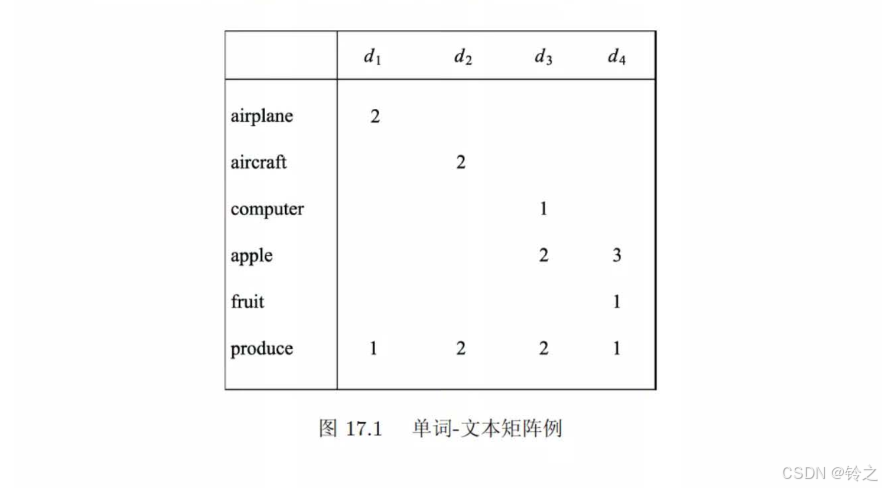
试将图17.1的例子进行潜在语义分析，并对结果进行观察。
在这里插入图片描述

# X=U*(Sigma*Vt)=T*Y
import numpy as np

# 保留两位小数，不使用科学计数法
np.set_printoptions(precision = 2, suppress = True)

def lsa_svd(X, k):
    """
    潜在语义分析的矩阵奇异值分解
    :param X: 单词-文本矩阵
    :param k: 话题数
    :return: 话题向量空间、文本集合在话题向量空间的表示
    """
    # 单词-文本矩阵X的奇异值分解
    U, S, Vt = np.linalg.svd(X)
    # 矩阵的截断奇异值分解，取前k个
    U = U[:, :k]
    S = np.diag(S[:k])
    Vt = Vt[:k, :] # 取V的前k列即为取V^T的前k行

    return U, np.dot(S, Vt)

X = [[2, 0, 0, 0], [0, 2, 0, 0], [0, 0, 1, 0], [0, 0, 2, 3], [0, 0, 0, 1], [1, 2, 2, 1]]
X = np.asarray(X)
T, Y = lsa_svd(X, 3)

print("单词话题矩阵T（话题空间）:\n", T)
print("话题文本矩阵Y（文本在话题空间的表示）:\n", Y)

单词话题矩阵T（话题空间）:
 [[-0.08 -0.28  0.89]
 [-0.16 -0.57 -0.45]
 [-0.14  0.01 -0.  ]
 [-0.73  0.55  0.  ]
 [-0.15  0.18  0.  ]
 [-0.63 -0.51 -0.  ]]
话题文本矩阵Y（文本在话题空间的表示）:
 [[-0.79 -1.57 -2.86 -2.96]
 [-1.08 -2.15  0.1   1.33]
 [ 1.79 -0.89 -0.    0.  ]]

在假设话题个数为3的情况下，单词airplane在话题3上的权值最大为0.89，表示单词airplane在话题3中的重要度最高；文本 $d 2$ 在话题2中的权值最大为-2.15，表示话题2在文本 $d 2$ 中的重要度最高。

# 或者可以直接使用sklearn的截断奇异值分解类
from sklearn.decomposition import TruncatedSVD

# 可惜的是这个类不会显式地计算出左奇异矩阵U
svd = TruncatedSVD(n_components=3, n_iter=7, random_state=42)  
svd.fit(X)
Sigma = np.diag(svd.singular_values_)
# svd.components_返回的是已截断的Vt，形状为(n_components,X的列数)
Y = np.dot(Sigma, svd.components_)
print("话题文本矩阵Y（文本在话题空间的表示）:\n", Y)

话题文本矩阵Y（文本在话题空间的表示）:
 [[ 0.79  1.57  2.86  2.96]
 [ 1.08  2.15 -0.1  -1.33]
 [ 1.79 -0.89 -0.    0.  ]]

习题17.2

给出损失函数是散度损失时的非负矩阵分解（潜在语义分析）的算法。
在这里插入图片描述
损失函数是散度损失时的非负矩阵分解算法

import numpy as np


class DivergenceNmfLsa:
    def __init__(self, max_iter=1000, tol=1e-6, random_state=0):
        """
        损失函数是散度损失时的非负矩阵分解
        :param max_iter: 最大迭代次数
        :param tol: 容差
        :param random_state: 随机种子
        """
        self.max_iter = max_iter
        self.tol = tol
        self.random_state = random_state
        np.random.seed(self.random_state)

    def _init_param(self, X, k):
        self.__m, self.__n = X.shape
        self.__W = np.random.random((self.__m, k))
        self.__H = np.random.random((k, self.__n))

    def _div_loss(self, X, W, H):
        Y = np.dot(W, H)
        loss = 0
        for i in range(self.__m):
            for j in range(self.__n):
                loss += (X[i][j] * np.log(X[i][j] / Y[i][j])
                         if X[i][j] * Y[i][j] > 0 else 0) - X[i][j] + Y[i][j]

        return loss

    def fit(self, X, k):
        """
        :param X: 单词-文本矩阵
        :param k: 话题个数
        :return:
        """
        # (1)初始化
        self._init_param(X, k)
        # (2.c)计算散度损失
        loss = self._div_loss(X, self.__W, self.__H)

        for _ in range(self.max_iter):
            # (2.a)更新W的元素
            WH = np.dot(self.__W, self.__H)
            for i in range(self.__m):
                for l in range(k):
                    s1 = sum(self.__H[l][j] * X[i][j] / WH[i][j]
                             for j in range(self.__n))
                    s2 = sum(self.__H[l][j] for j in range(self.__n))
                    self.__W[i][l] *= s1 / s2

            # (2.b)更新H的元素
            WH = np.dot(self.__W, self.__H)
            for l in range(k):
                for j in range(self.__n):
                    s1 = sum(self.__W[i][l] * X[i][j] / WH[i][j]
                             for i in range(self.__m))
                    s2 = sum(self.__W[i][l] for i in range(self.__m))
                    self.__H[l][j] *= s1 / s2

            new_loss = self._div_loss(X, self.__W, self.__H)
            if abs(new_loss - loss) < self.tol:
                break

            loss = new_loss

        return self.__W, self.__H

X = np.array([[2, 0, 0, 0],
              [0, 2, 0, 0],
              [0, 0, 1, 0],
              [0, 0, 2, 3],
              [0, 0, 0, 1],
              [1, 2, 2, 1]])

# 设置精度为2
np.set_printoptions(precision=2, suppress=True)
# 假设话题的个数是3个
k = 3
div_nmf = DivergenceNmfLsa(max_iter=200, random_state=2022)
W, H = div_nmf.fit(X, k)
print("话题空间W：")
print(W)
print("文本在话题空间的表示H：")
print(H)

话题空间W：
[[0.   0.   1.39]
 [0.   1.47 0.  ]
 [0.35 0.   0.  ]
 [1.77 0.   0.  ]
 [0.35 0.   0.  ]
 [1.06 1.47 0.7 ]]
文本在话题空间的表示H：
[[0.   0.   1.41 1.41]
 [0.   1.36 0.   0.  ]
 [1.44 0.   0.   0.  ]]

习题17.3，习题17.4

解答见链接

使用书籍：李航《机器学习方法》
习题解答：https://datawhalechina.github.io/statistical-learning-method-solutions-manual/#/