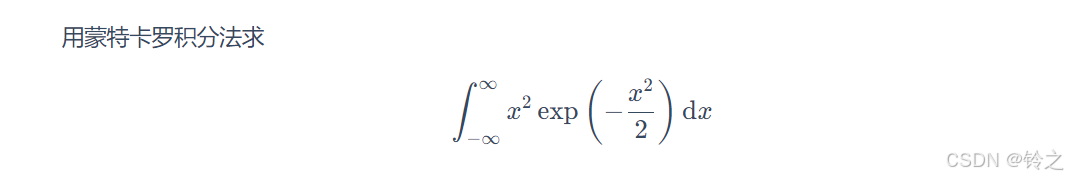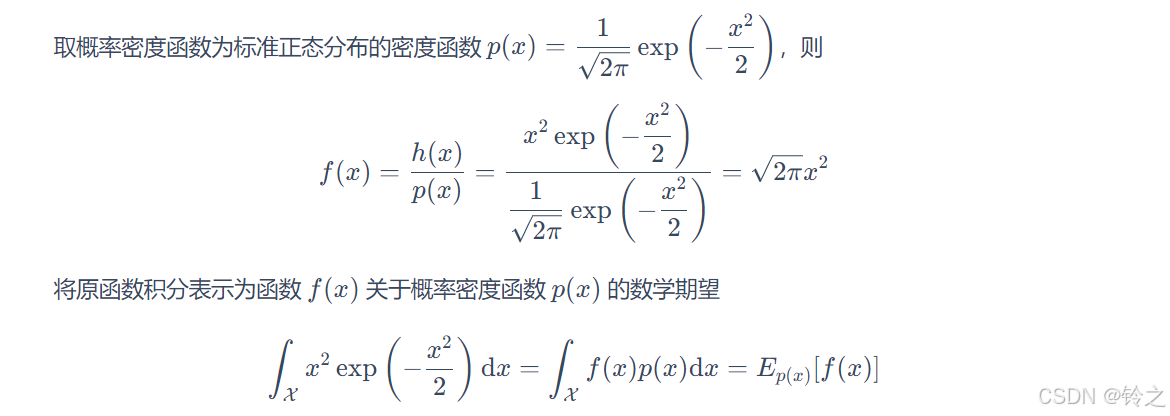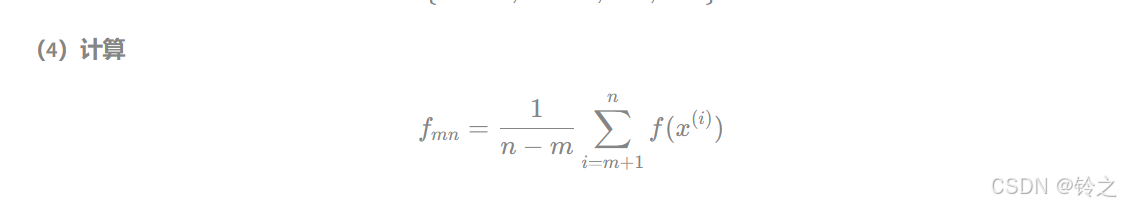本章学习使用书籍：李航老师的《机器学习方法》

配合观看视频：蒙特卡洛（Monte Carlo, MCMC）方法的原理和应用P1、P2和机器学习-白板推导系列(十三)-MCMC（Markov Chain Monte Carlo）

其他博客链接：

https://cosx.org/2013/01/lda-math-mcmc-and-gibbs-sampling

https://www.cnblogs.com/pinard/p/6638955.html

https://zhuanlan.zhihu.com/p/37121528

把以上都看完就无敌了孩子。

本章概要：

1. 蒙特卡罗法是通过基于概率模型的抽样进行数值近似计算的方法，蒙特卡罗法可以用于概率分布的抽样、概率分布数学期望的估计、定积分的近似计算。

随机抽样是蒙特卡罗法的一种应用，有直接抽样法、接受拒绝抽样法等。接受拒绝法的基本想法是，找一个容易抽样的建议分布，其密度函数的数倍大于等于想要抽样的概率分布的密度函数。按照建议分布随机抽样得到样本，再按要抽样的概率分布与建议分布的倍数的比例随机决定接受或拒绝该样本，循环执行以上过程。

马尔可夫链蒙特卡罗法数学期望估计是蒙特卡罗法的另一种应用，按照概率分布$p(x)$抽取随机变量$x$的$n$个独立样本，根据大数定律可知，当样本容量增大时，函数的样本均值以概率1收敛于函数的数学期望

$${\hat{f}}_n\to E_{p(x)}[f(x)],n\to \infty$$

计算样本均值${\hat{f}}_n$，作为数学期望$E_{p(x)}[f(x)]$的估计值。

2. 马尔可夫链是具有马尔可夫性的随机过程$$P(X_t|X_0{X}_1\cdots X_{t-1})=P(X_t|X_{t-1}),t=1,2,\cdots$$
   通常考虑时间齐次马尔可夫链。有离散状态马尔可夫链和连续状态马尔可夫链，分别由概率转移矩阵$P$和概率转移核$p(x,y)$定义。

满足$\pi =P\pi$或$\pi (y)=\int p(x,y)\pi (x)dx$的状态分布称为马尔可夫链的平稳分布。

马尔可夫链有不可约性、非周期性、正常返等性质。一个马尔可夫链若是不可约、非周期、正常返的，则该马尔可夫链满足遍历定理。当时间趋于无穷时，马尔可夫链的状态分布趋近于平稳分布，函数的样本平均依概率收敛于该函数的数学期望。

$${\lim }_{t\to \infty }P(X_t=i|X_0=j)={\pi }_i,i=1,2,\cdots ;j=1,2$$
$${\hat{f}}_t\to E_{\pi }[f(X)],t\to \infty$$
可逆马尔可夫链是满足遍历定理的充分条件。

3. 马尔可夫链蒙特卡罗法是以马尔可夫链为概率模型的蒙特卡罗积分方法，其基本想法如下：

（1）在随机变量$x$的状态空间$\chi$上构造一个满足遍历定理条件的马尔可夫链，其平稳分布为目标分布$p(x)$；

（2）由状态空间的某一点$X_0$出发，用所构造的马尔可夫链进行随机游走，产生样本序列$X_1,X_2,\cdots ,X_t,\cdots$；

（3）应用马尔可夫链遍历定理，确定正整数$m$和$n(m<n)$，得到样本集合 { x m + 1 , x m + 2 , ⋯   , x n } \{ x _ { m + 1 } , x _ { m + 2 } , \cdots , x _ { n } \} {xm+1​,xm+2​,⋯,xn​}，进行函数$f(x)$的均值（遍历均值）估计：
$$\hat{E}f=\frac{1}{n-m}\sum _{i=m+1}^{n}f(x_i)$$

4. Metropolis-Hastings算法是最基本的马尔可夫链蒙特卡罗法。假设目标是对概率分布$p(x)$进行抽样，构造建议分布$q(x,x^{\prime })$，定义接受分布$\alpha (x,x^{\prime })$进行随机游走，假设当前处于状态$x$，按照建议分布$q(x,x^{\prime })$机抽样，按照概率$\alpha (x,x^{\prime })$接受抽样，转移到状态 $x^{\prime }$，按照概率$1-\alpha (x,x^{\prime })$拒绝抽样，停留在状态$x$，持续以上操作，得到一系列样本。这样的随机游走是根据转移核为$p(x,x^{\prime })=q(x,x^{\prime })\alpha (x,x^{\prime })$的可逆马尔可夫链（满足遍历定理条件）进行的，其平稳分布就是要抽样的目标分布$p(x)$。

5. 吉布斯抽样（Gibbs sampling）用于多元联合分布的抽样和估计吉布斯抽样是单分量 Metropolis-Hastings-算法的特殊情况。这时建议分布为满条件概率分布$$q(x,x^{\prime })=p(x_j^{\prime }|x_{-j})$$
   吉布斯抽样的基本做法是，从联合分布定义满条件概率分布，依次从满条件概率分布进行抽样，得到联合分布的随机样本。假设多元联合概率分布为$p(x)=p(x_1,x_2,\cdots ,x_k)$，吉布斯抽样从一个初始样本$x^{(0)}=(x_1^{(0)},x_2^{(0)},\cdots ,x_k^{(0)}{)}^T$出发，不断进行迭代，每一次迭代得到联合分布的一个样本$x^{(i)}=(x_1^{(i)},x_2^{(i)},\cdots ,x_k^{(i)}{)}^T$，在第$i$次迭代中，依次对第$j$个变量按照满条件概率分布随机抽样$p(x_j|x_1^{(i)},\cdots ,x_{j-1}^{(i)},x_{j+1}^{(i-1)},\cdots ,x_k^{(i-1)}),j=1,2,\cdots ,k$，得到$x_j^{(i)}$最终得到样本序列 { x ( 0 ) , x ( 1 ) , ⋯   , x ( n ) } \{ x ^ { ( 0 ) } , x ^ { ( 1 ) } , \cdots , x ^ { ( n ) } \} {x(0),x(1),⋯,x(n)}。

本文只挑几个课后习题。

习题19.1

import numpy as np


class MonteCarloIntegration:
    def __init__(self, func_f, func_p):
        # 所求期望的函数
        self.func_f = func_f
        # 抽样分布的概率密度函数
        self.func_p = func_p

    def solve(self, num_samples):
        """
        蒙特卡罗积分法
        :param num_samples: 抽样样本数量
        :return: 样本的函数均值
        """
        samples = self.func_p(num_samples)
        y = self.func_f(samples)
        return np.sum(y) / num_samples


def func_f(x):
    """定义函数f"""
    return x**2 * np.sqrt(2 * np.pi)  # 即h(x)/p(x)得到的函数表达式


def func_p(n):
    """p(x)是标准正态分布，随机抽样n个观测"""
    return np.random.standard_normal(int(n))


# 设置样本数量
num_samples = 1e6

# 使用蒙特卡罗积分法进行求解
monte_carlo_integration = MonteCarloIntegration(func_f, func_p)
result = monte_carlo_integration.solve(num_samples)
print("抽样样本数量:", num_samples)
print("近似解:", result)

抽样样本数量: 1000000.0
近似解: 2.508167414386113

习题19.6

 从一般的Metropolis-Hastings算法推导出单分量Metropolis-Hastings算法。

习题19.7

 假设进行伯努利实验，后验概率为 $P(\theta |y)$，其中变量 y ∈ { 0 , 1 } y \in \{ 0, 1 \} y∈{0,1} 表示实验可能的结果，变量 $\theta$ 表示结果为 1 的概率。再假设先验概率 $P(\theta )$ 遵循 Beta 分布 $B(\alpha ,\beta )$，其中 $\alpha =1,\beta =1$；似然函数 $P(y|\theta )$ 遵循二项分布$\text{Bin}(n,k,\theta )$，其中 $n=10,k=4$，即实验进行 10 次其中结果为 1 的次数为 4。试用 Metropolis-Hastings 算法求后验概率分布 $P(\theta |y)\propto P(\theta )P(y|\theta )$ 的均值和方差。（提示：可采用 Metropolis 选择，即假设建议分布是对称的。）

解答：
为了使用 Metropolis-Hastings 算法求后验概率分布 $P(\theta |y)$，需要进行以下几个步骤：

1. 定义先验分布和似然函数：

   • 先验分布 $P(\theta )$ 遵循 Beta 分布 $B(\alpha ,\beta )$，其中 $\alpha =1,\beta =1$，即均匀分布。
   • 似然函数 $P(y|\theta )$ 是二项分布 $\text{Bin}(n,k,\theta )$，其中 $n=10,k=4$。

2. 定义后验分布：
   $$P(\theta |y)\propto P(\theta )P(y|\theta )$$

3. 选择提议分布：
   使用对称的提议分布，例如正态分布。

4. 实现 Metropolis-Hastings 算法：

   • 初始化 $\theta$ 值。
   • 迭代执行以下步骤：
     • 从提议分布中采样一个新的 ${\theta }^{\prime }$。
     • 计算接受率：
       $$\alpha =\min \left(1,\frac{P({\theta }^{\prime }|y)}{P(\theta |y)}\right)$$
     • 根据接受率决定是否接受新的 ${\theta }^{\prime }$。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta, binom

# 定义先验分布的参数
alpha_prior = 1
beta_prior = 1

# 定义似然函数的参数
n = 10
k = 4

# 定义后验分布
def posterior(theta):
    if 0 <= theta <= 1:
        prior = beta.pdf(theta, alpha_prior, beta_prior)
        likelihood = binom.pmf(k, n, theta)
        return prior * likelihood
    else:
        return 0

# Metropolis-Hastings 算法
def metropolis_hastings(posterior, initial_theta, num_samples, proposal_width):
    samples = []
    theta_current = initial_theta
    for _ in range(num_samples):
        theta_proposed = np.random.normal(theta_current, proposal_width)
        acceptance_ratio = posterior(theta_proposed) / posterior(theta_current)
        if np.random.rand() < acceptance_ratio:
            theta_current = theta_proposed
        samples.append(theta_current)
    return np.array(samples)

# 设置算法参数
initial_theta = 0.5
num_samples = 10000
proposal_width = 0.1

# 运行 Metropolis-Hastings 算法
samples = metropolis_hastings(posterior, initial_theta, num_samples, proposal_width)

# 后验分布的均值和方差
half=int(num_samples/2)
mean_theta = np.mean(samples[half:])
var_theta = np.var(samples[half:])

print(f'后验分布均值: {mean_theta}')
print(f'后验分布方差: {var_theta}')

# 绘制后验分布的样本直方图
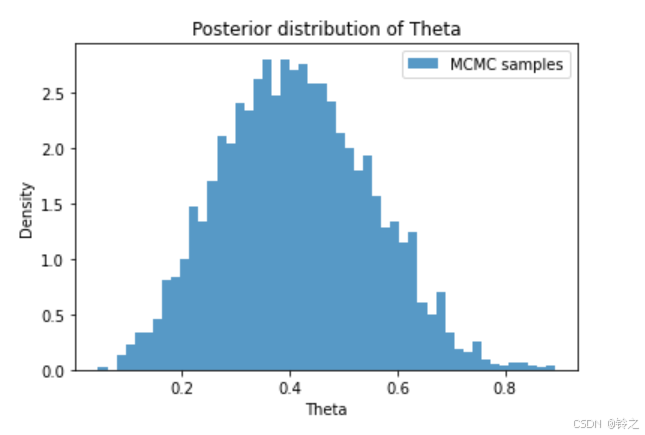
plt.hist(samples[half:], bins=50, density=True, alpha=0.75, label='MCMC samples')
plt.xlabel('Theta')
plt.ylabel('Density')
plt.title('Posterior distribution of Theta')
plt.legend()
plt.show()

后验分布均值: 0.4127077514777162
后验分布方差: 0.019117645067499734

习题19.8

 设某试验可能有五种结果，其出现的概率分别为
$$\frac{\theta }{4}+\frac{1}{8},\frac{\theta }{4},\frac{\eta }{4},\frac{\eta }{4}+\frac{3}{8},\frac{1}{2}(1-\theta -\eta )$$
模型含有两个参数 $\theta$ 和 $\eta$，都介于 0 和 1 之间。现有 22 次试验结果的观测值为
$$y=(y_1,y_2,y_3,y_4,y_5)=(14,1,1,1,5)$$
其中 $y_i$ 表示 22 次试验中第 $i$ 个结果出现的次数，$i=1,2,\cdots ,5$。试用吉布斯抽样估计参数 $\theta$ 和 $\eta$ 的均值和方差。

为了使用吉布斯抽样估计参数 $\theta$ 和 $\eta$ 的均值和方差，我们需要以下几个步骤：

1. 定义似然函数和联合后验分布。
2. 选择初始值。
3. 迭代进行吉布斯抽样：
   • 依次从条件后验分布 $P(\theta |\eta ,y)$ 和 $P(\eta |\theta ,y)$ 中抽样。

似然函数和联合后验分布

首先，给定观测数据 $y=(y_1,y_2,y_3,y_4,y_5)=(14,1,1,1,5)$，似然函数为：
$$P(y|\theta ,\eta )={\left(\frac{\theta }{4}+\frac{1}{8}\right)}^{y_1}{\left(\frac{\theta }{4}\right)}^{y_2}{\left(\frac{\eta }{4}\right)}^{y_3}{\left(\frac{\eta }{4}+\frac{3}{8}\right)}^{y_4}{\left(\frac{1}{2}(1-\theta -\eta )\right)}^{y_5}$$

为了简化计算，我们假设先验分布为均匀分布 $P(\theta )=1$ 和 $P(\eta )=1$，因此后验分布正比于似然函数。

$$P(\theta ,\eta |y)\propto P(y|\theta ,\eta )\cdot P(\theta )\cdot P(\eta )$$

吉布斯抽样

吉布斯抽样是一个马尔可夫链蒙特卡罗（MCMC）算法，用于从高维联合分布中抽样。它通过依次从每个条件分布中抽样来实现。对于参数 $\theta$ 和 $\eta$，我们需要知道它们的条件后验分布。

1. 从 $P(\theta |\eta ,y)$ 抽样：
   $$P(\theta |\eta ,y)\propto {\left(\frac{\theta }{4}+\frac{1}{8}\right)}^{14}\left(\frac{\theta }{4}\right){\left(\frac{1}{2}(1-\theta -\eta )\right)}^5$$

2. 从 $P(\eta |\theta ,y)$ 抽样：
   $$P(\eta |\theta ,y)\propto \left(\frac{\eta }{4}\right)\left(\frac{\eta }{4}+\frac{3}{8}\right){\left(\frac{1}{2}(1-\theta -\eta )\right)}^5$$

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta

# 观测值
y = np.array([14, 1, 1, 1, 5])
n_iter = 10000  # 迭代次数
burn_in = 1000  # 烧入（收敛）步数

# 初始化参数
theta_samples = np.zeros(n_iter)
eta_samples = np.zeros(n_iter)
theta_samples[0] = np.random.rand()
eta_samples[0] = np.random.rand()


# 定义抽样函数
def sample_theta(eta, y):
    a = y[0] + y[1] + 1
    b = y[4] + 1
    return beta.rvs(a, b) * (1 - eta) # 贝塔分布产生的值为[0,1]之间，乘以(1-eta)以确保theta+eta<1


def sample_eta(theta, y):
    a = y[2] + y[3] + 1
    b = y[4] + 1
    return beta.rvs(a, b) * (1 - theta)


# 吉布斯抽样
for i in range(1, n_iter):
    theta_samples[i] = sample_theta(eta_samples[i - 1], y)
    eta_samples[i] = sample_eta(theta_samples[i], y)

# 去掉烧入阶段的样本
theta_samples_post_burn_in = theta_samples[burn_in:]
eta_samples_post_burn_in = eta_samples[burn_in:]

# 计算均值和方差
mean_theta = np.mean(theta_samples_post_burn_in)
var_theta = np.var(theta_samples_post_burn_in)
mean_eta = np.mean(eta_samples_post_burn_in)
var_eta = np.var(eta_samples_post_burn_in)

print(f'θ 的均值: {mean_theta}, 方差: {var_theta}')
print(f'η 的均值: {mean_eta}, 方差: {var_eta}')

# 绘制样本直方图
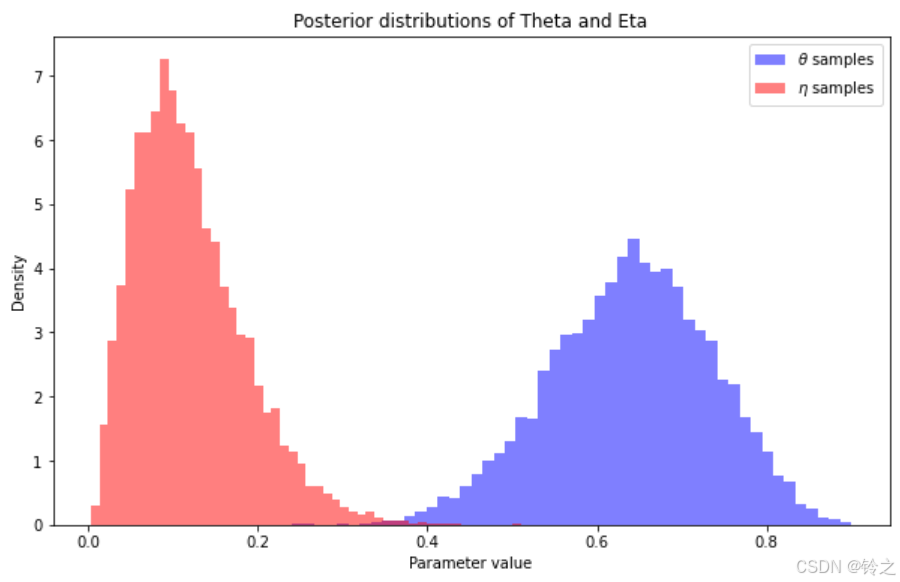
plt.figure(figsize=(10, 6))

plt.hist(theta_samples_post_burn_in,
         bins=50,
         density=True,
         alpha=0.5,
         label='$\\theta$ samples',
         color='blue')
plt.hist(eta_samples_post_burn_in,
         bins=50,
         density=True,
         alpha=0.5,
         label='$\\eta$ samples',
         color='red')

plt.xlabel('Parameter value')
plt.ylabel('Density')
plt.title('Posterior distributions of Theta and Eta')
plt.legend()
plt.show()

θ 的均值: 0.6393311463493639, 方差: 0.009050636891319451
η 的均值: 0.11999694894828164, 方差: 0.004142201497725771

代码解释:

1. 初始化参数和样本数组：

   • theta_samples 和 eta_samples 用于存储每次迭代的抽样结果。
   • 随机初始化参数 $\theta$ 和 $\eta$。

2. 定义条件抽样函数：

   • sample_theta 函数根据当前的 $\eta$ 和观测值 $y$ 抽样新的 $\theta$ 值。
   • sample_eta 函数根据当前的 $\theta$ 和观测值 $y$ 抽样新的 $\eta$ 值。

3. 吉布斯抽样迭代：

   • 依次从条件分布 $P(\theta |\eta ,y)$ 和 $P(\eta |\theta ,y)$ 中抽样新的 $\theta$ 和 $\eta$，并将结果存储到样本数组中。

4. 计算结果：

   • 计算 $\theta$ 和 $\eta$ 样本的均值和方差。
   • 绘制 $\theta$ 和 $\eta$ 样本的后验分布直方图。

通过执行以上代码，可以得到 $\theta$ 和 $\eta$ 的后验分布的样本，并估计它们的均值和方差。

附：本来想安装关于MCMC的库pymc3，可死活安装不成功，整憔悴了！
习题参考： https://datawhalechina.github.io/statistical-learning-method-solutions-manual/#/chapter19/ch19