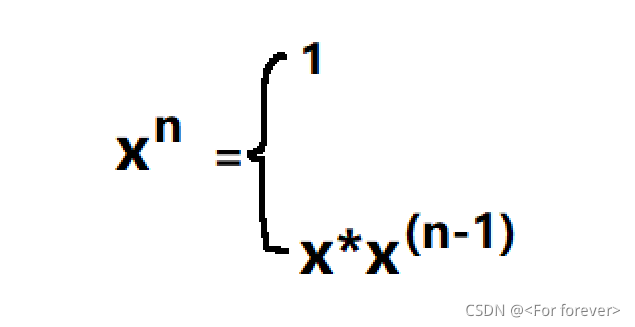前言

Hello,everyone! forever 上次对函数基础部分做了归纳整理，今天就来说说函数的递归。希望能给初学者提供一些帮助，如有不足之处也望大佬们评价并批评指正。

正文

一、什么是递归

在一个过程或函数执行过程中直接或间接的调用自己本身，这就称为递归调用。C 语言中允许函数递归，在函数中直接调用函数本身称为直接递归调用。在函数中调用其他函数，其他函数又调用原函数，称为间接递归调用。
如下图解释：

如下例题解释：
例题，求一个数 x 的 n 次方：

在求解 xⁿ中使用了 x^(n-1) ，即要计算出 xⁿ，必须先计算求出 x^(n-1)，而要知道 x^(n-1)，必须先求出 x^(n-2)，以此类推，直到求出 x⁰为止。再以此为基础，返回来求 xⁿ。这种算法就称为递归算法，递归算法可以将复杂问题简单化。

二、递归的关键点和优缺点

1、递归的两个关键点

递归边界和递归公式

2、递归的优点

递归可以将大型复杂问题简单化转化成规模较小的问题，减少代码量。

3、递归的缺点

递归重复次数过多会出现栈溢出；而且过多的重复计算会降低效率。

4、递归的两个必要条件

（1）递归必须在一定的限制条件下进行；
（2）每次递归后都会越来越接近这个限制条件。

三、实际问题理解递归

1、按顺序打印一个数字的各位数

//顺序打印一个数的各个位数
#include<stdio.h>
void print(int n)
{
	if (n > 9)
	{
		print(n / 10);// print函数自己调用自己
	}
	printf("%d\n", n % 10);
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	print(n);
	return 0;
}

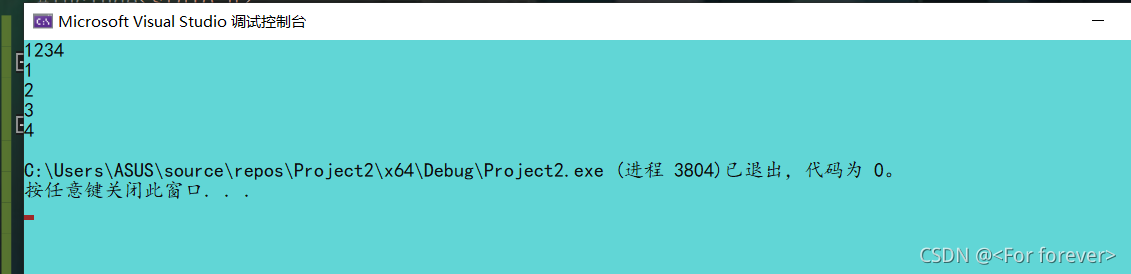
运行结果：

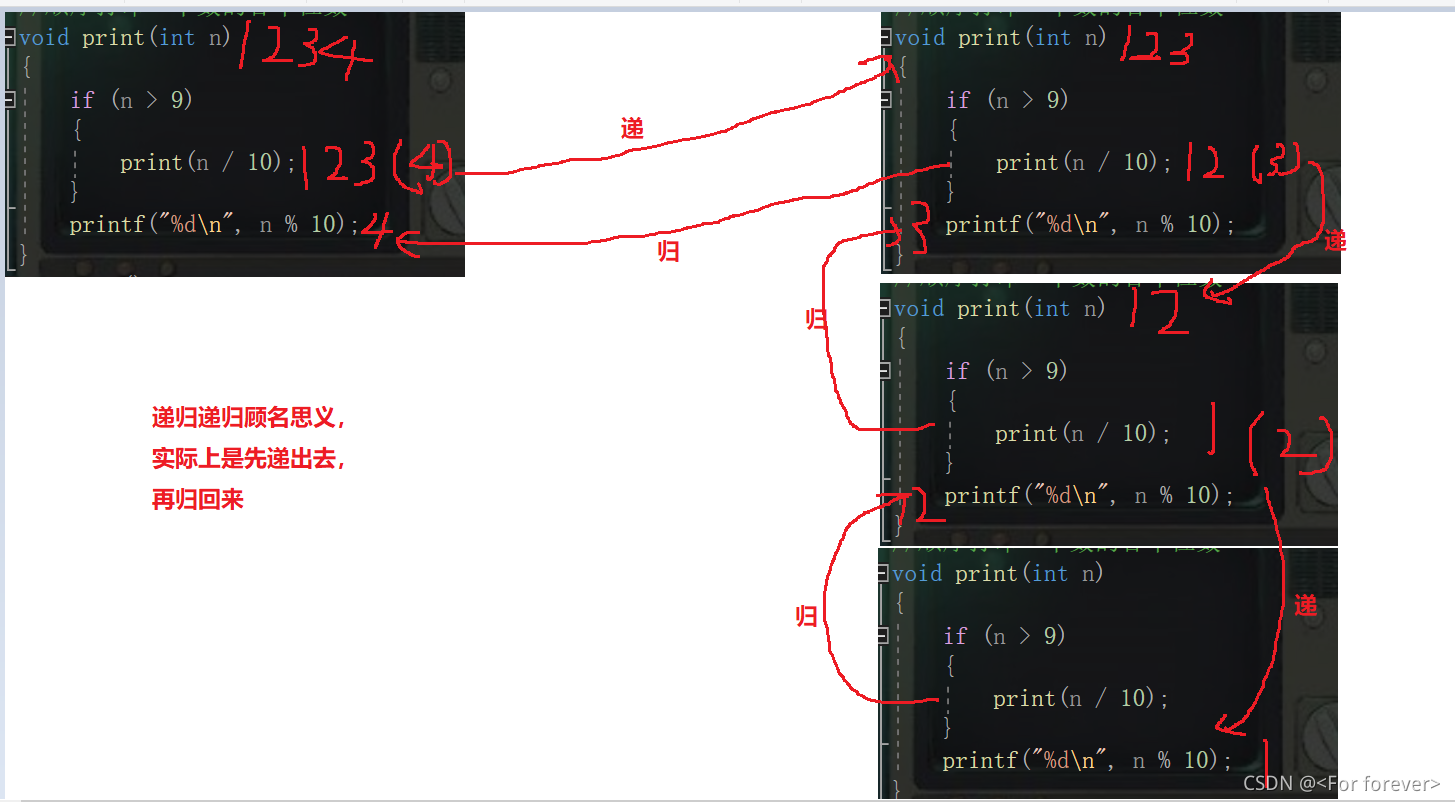
如下图解分析：

如上是利用递归来按顺序打印一个数的各个位数，其过程是通过递归先将其数目一位一位的拆开，然后再依次打印 1，2，3，4。

2、利用递归实现斐波那契数列

斐波那契数列又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……
（1）利用递归实现斐波那契数列

//递归实现斐波那契数列
#include<stdio.h>
int Fib(int n)
{
	if (n < 3)//递归实现条件
	{
		return 1;
	}
	else
	{
		return Fib(n - 1) + Fib(n - 2);//递归公式
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d", ret);
	return 0;
}

运行结果：

（2）非递归对比
相比之下，递归代码更加简洁、简便。

//非递归实现斐波那契数列
#include<stdio.h>
int Fib(int n)
{
	int a = 1;
	int b = 0;
	if (n < 2)
	{
		return 1;
	}
	else
	{
		for (int i = 2; i <= n; i++)
		{
			a = a + b;
			b = a - b;
		}
		return a;
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret=Fib(n);
	printf("%d\n", ret);
	return 0;
}

运行结果：

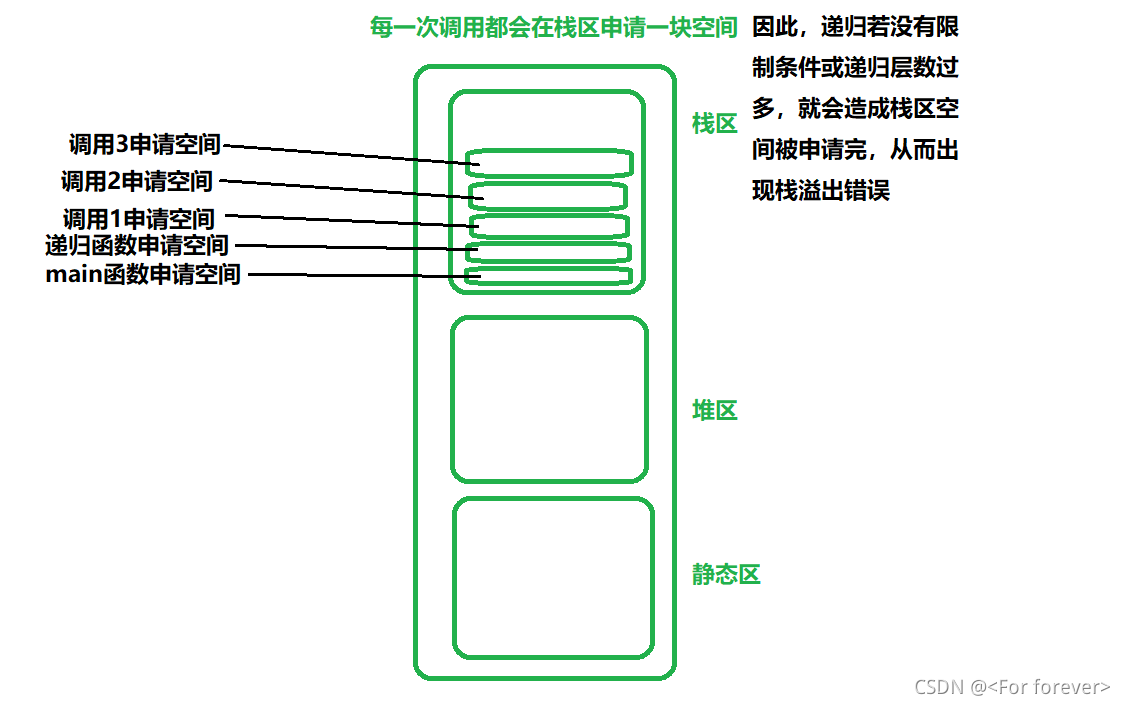
**这两个简单的例子就能明显反映递归的思想以及递归算法。调用的层数称为递归的深度。函数的递归是分两个阶段完成。第一个阶段是逐层调用，调用函数自身；第二个阶段是逐层返回，返回到调用该层的位置继续执行后续操作。递归调用是多重嵌套的一种特殊情况，每次递归调用都要用堆栈保护主调层的现场和返回地址。**即每一次调用都会在内存的栈区申请块空间，如下图：

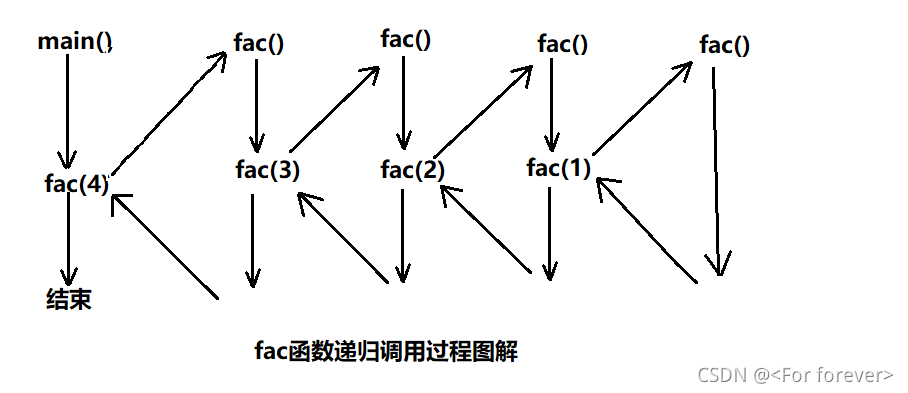
3、图解递归调用过程

四、递归、循环和迭代

1、迭代介绍及与其他的区别

迭代是利用已知的变量值，根据递推公式不断演变得到变量新值的编程思想。它是函数内部某段代码实现循环。
迭代与普通循环的区别：迭代循环代码中参与运算的变量同时是保存结果的变量，当前保存的结果作为下一次循环计算的初始值。

2、用斐波那契数列区分仨

（1）普通循环实现斐波那契数列

#include<stdio.h>
int Fib(int n)
{
	int a = 1;
	int b = 0;
	if (n < 2)
	{
		return 1;
	}
	else
	{
		for (int i = 2; i <= n; i++)
		{
			a = a + b;
			b = a - b;
		}
		return a;
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret=Fib(n);
	printf("%d\n", ret);
	return 0;
}

运行结果：

（2）迭代实现斐波那契数列

#include<stdio.h>
int Fib(int a)
{
	int temp = 0;
	int m = 0, n = 1;
	if (a < 2)
	{
		return 1;
	}
	else
	{
		for (int i = 2; i <= a; i++)
		{
			temp = m + n;//迭代里用的变量 以及递推公式
			m = n;
			n = temp;
		}
		return temp;
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret=Fib(n);
	printf("%d\n", ret);
	return 0;
}

运行结果：

（3）递归实现斐波那契数列

#include<stdio.h>
int Fib(int n)
{
	if (n < 3)//递归实现条件
	{
		return 1;
	}
	else
	{
		return Fib(n - 1) + Fib(n - 2);//递归公式
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d", ret);
	return 0;
}

运行结果：

3、汉诺塔问题

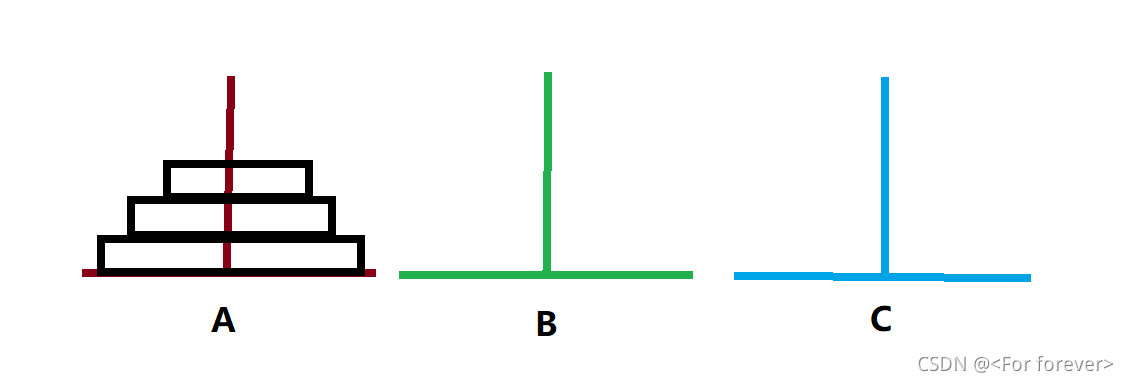
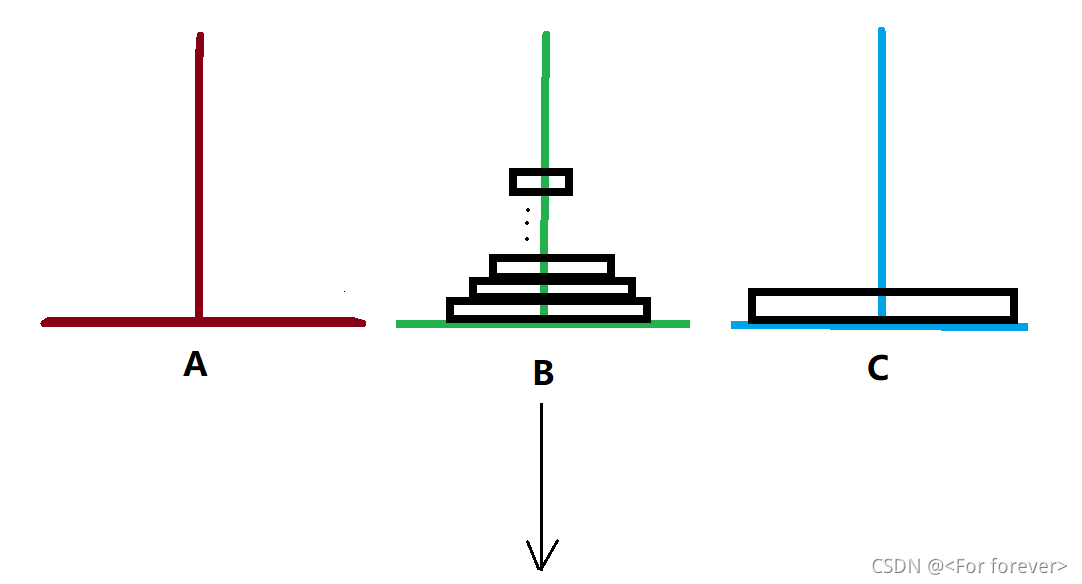
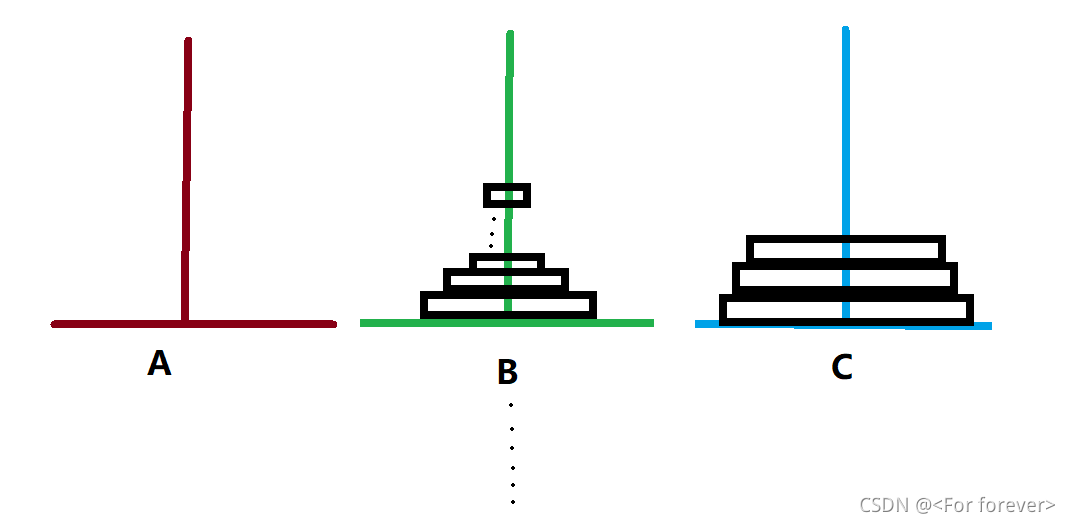
汉诺塔问题。这是一个经典的递归问题。问题是这样描述的：设有三个塔座（A、B、C、），在一个塔座（设为A塔）上有64个盘片，盘片大小不等，依下往上，按照从大到小顺序叠放着，如下图。现在要借助 B 塔将这些盘片移动到 C 塔去，要求在移动过程中，每个塔座的盘片始终保持大盘在下，小盘在上的叠放方式，每次只能移动一个盘片。

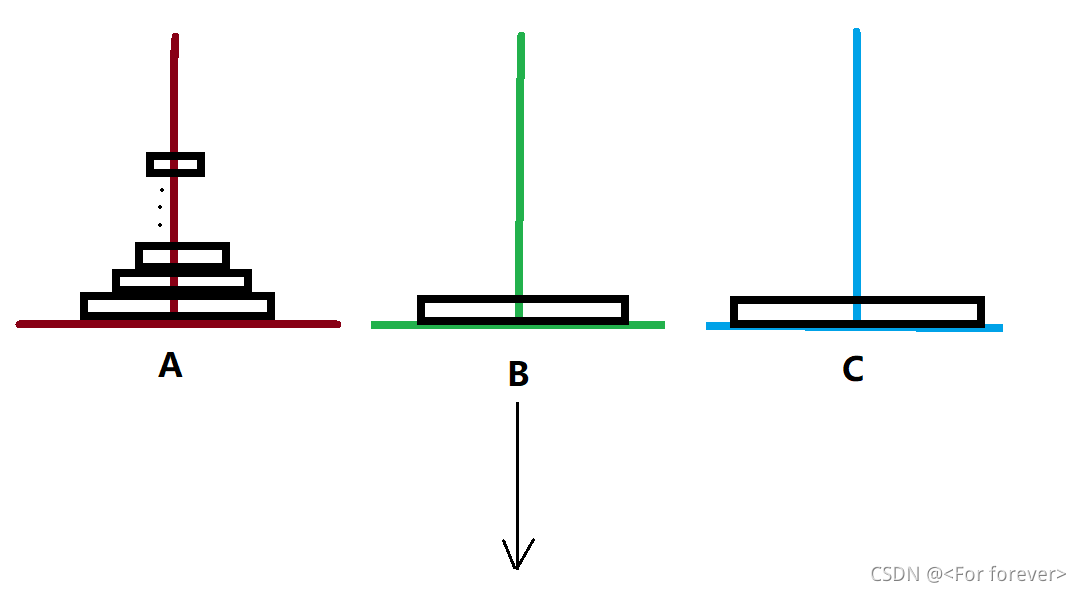
解决思路：可以设想（一）先将 A 上面的 63 片借助于 C 塔移动到 B 塔上，剩下的一片（化成 63 和 1 ）就可以移动到 C 塔上了；（二）这时再将 B 塔 63 片最上面的 62 片借助 C 塔移动到 A 塔，然后 B 塔上剩下的一片（化成 62 和 2 ）就可以直接移动到 C 塔了……同理，这样依次进行下去，就会完成整个移动。
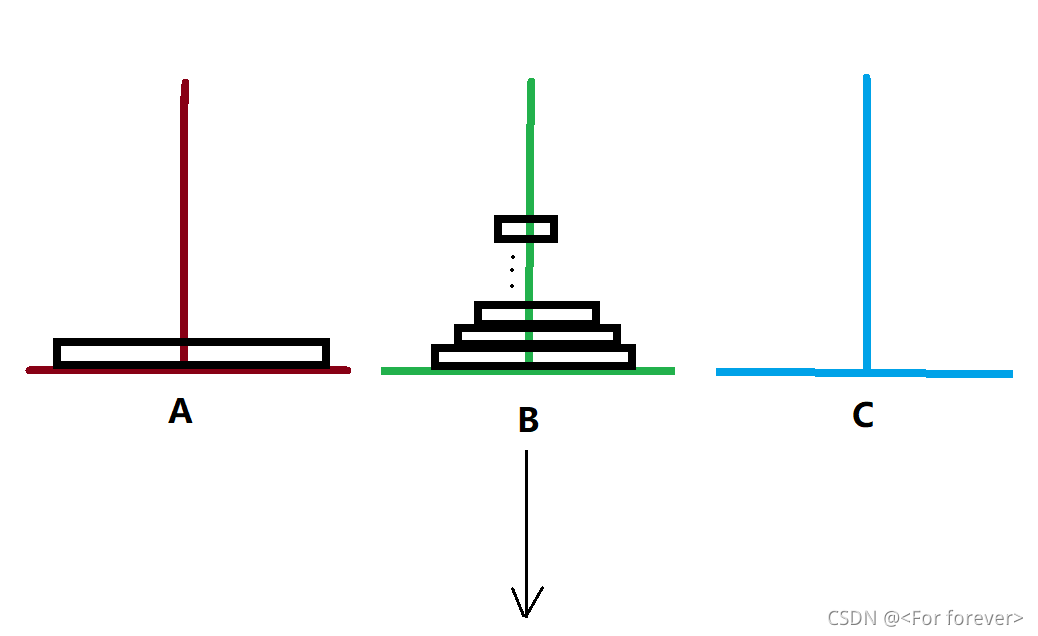
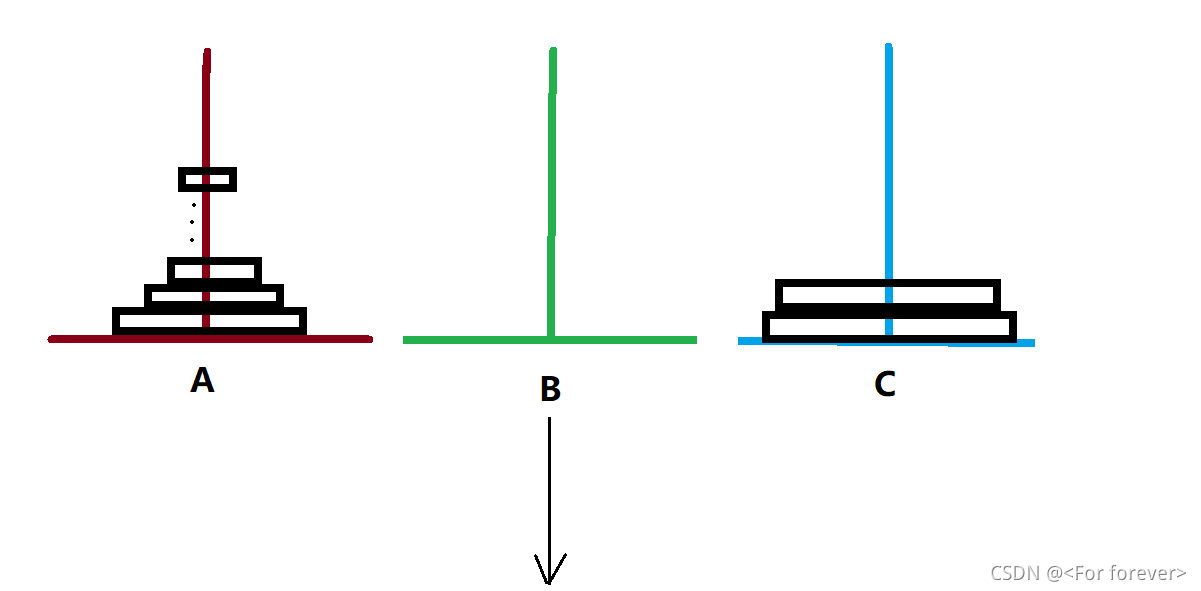
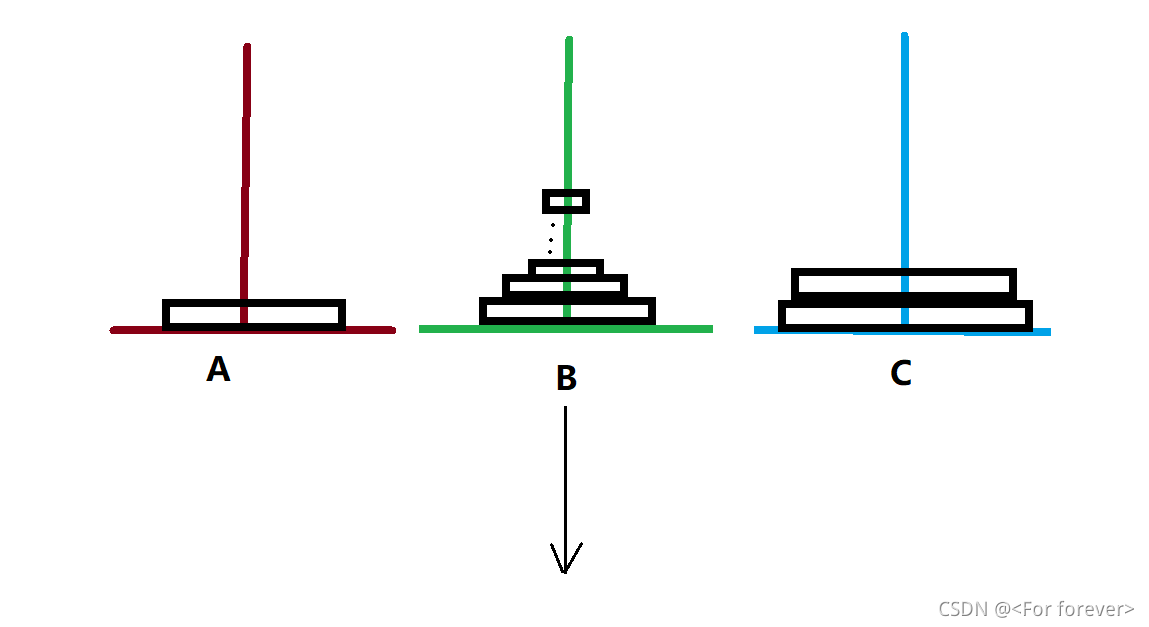
下面来个图解分析：





如上图实现：假设将 n 个盘片按规定从 A 塔移至到 C 塔，可以按以下步骤：
（1）将 A 上面的 n-1 个盘片借助 C 全部移到 B 上；
（2）然后再将最后第 n 个移动到 C 上；
（3）把 B 塔上的 n-1 个盘片借助 A 移动到 C ；
程序如下：

//递归实现汉诺塔问题
#include <stdio.h>
void hanoi(int n, char x, char y, char z)
{
	if (n == 1)
	{
		printf("%c—>%c\n", x, z);
	}
	else
	{
		hanoi(n - 1, x, z, y);
		printf("%c—>%c\n", x, z);
		hanoi(n - 1, y, x, z);
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	hanoi(n, 'A', 'B', 'C');
	return 0;
}

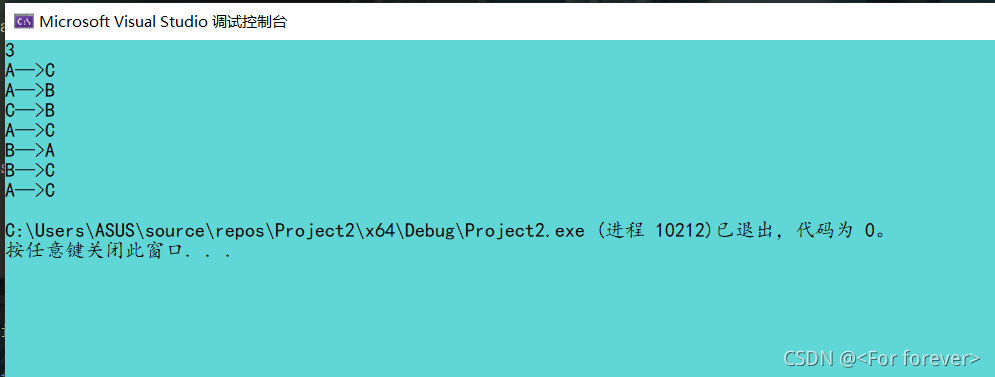
运行结果：

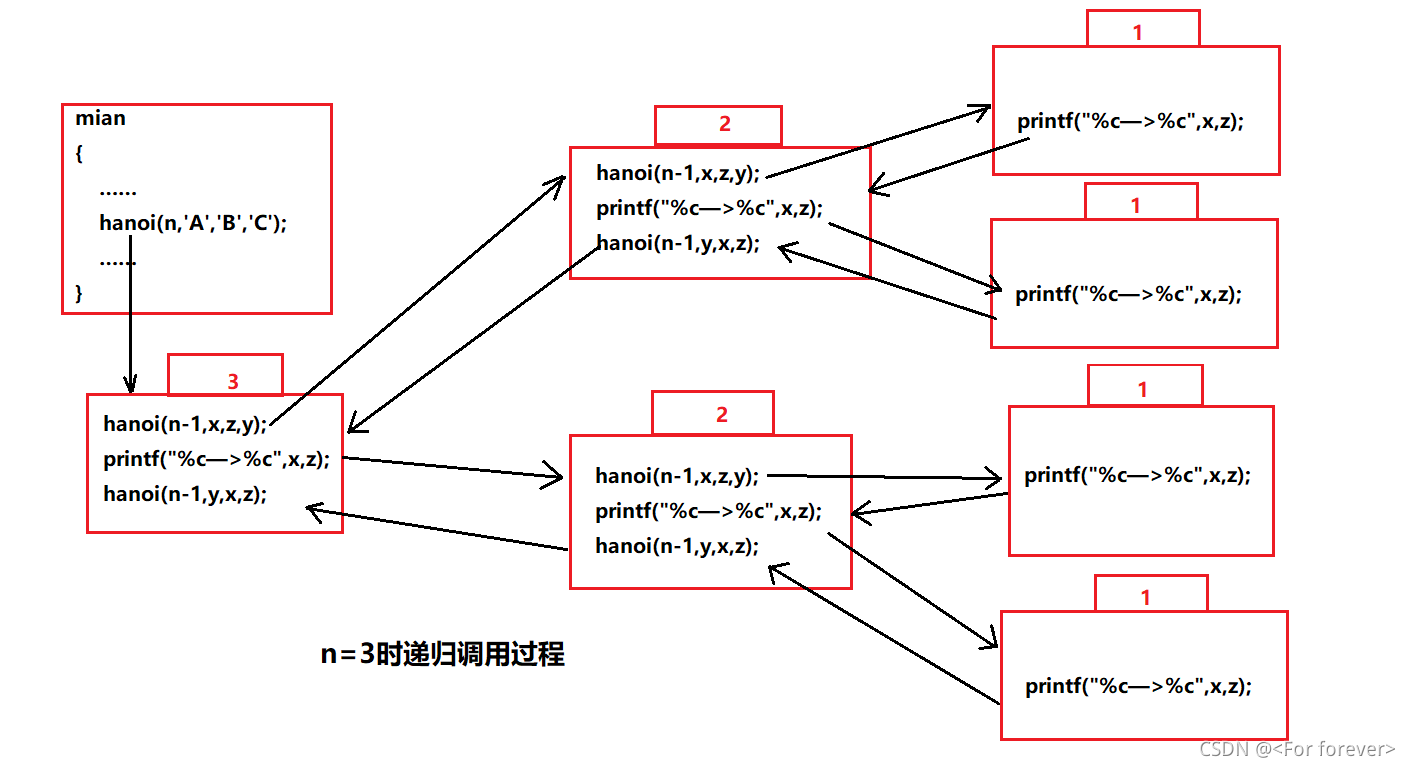
本程序只是输出了盘片的移动顺序，用它代表盘片移动的过程。这里通过递归算法用简单的过程去解决一个复杂的问题。如下递归调用过程详解图：

结语

OK! 目前就给大家介绍到这里，希望能给大家带来一些帮助哈！如有不足或错误之处，请大家多多指导！
谢谢观看！再见啦！
以上代码均可运行，所用编译环境为 vs2019 ,运行时注意加上编译头文件#define _CRT_SECURE_NO_WARNINGS 1