Hyperbolic Representation Learning: Revisiting and Advancing
论文地址和代码地址
论文地址:https://arxiv.org/pdf/2306.09118
代码地址:https://github.com/marlin-codes/HIE
1 介绍
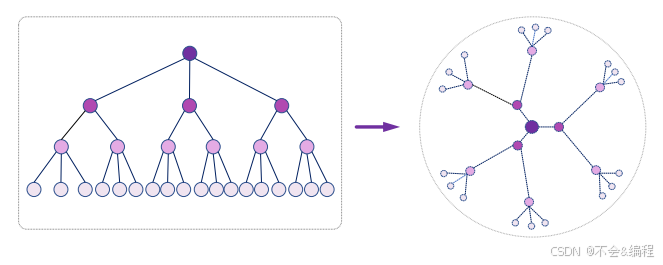
在利用双曲空间时,目标是提取数据中固有的层次信息。如下图所示,预期的学习目标包括优化父节点与其各自后代节点的关系,即将根节点推向双曲空间原点,同时将叶节点放置在离双曲空间原点更远的位置。
本文的贡献:
-
我们提出了一种位置跟踪策略,揭示了双曲学习过程与传统理解之间的显著差异,为双曲表示学习过程提供了新的视角。
-
引入了一种新颖的方法,用于从双曲嵌入中推断隐式的层次结构。它直接从嵌入中提取层次信息,省去了额外输入或注释的需求。
-
提出了一种简单而有效的方法,利用推断出的层次结构推进双曲表示学习。我们的方法与现有的双曲模型无缝集成,并且不会引入额外的模型参数,具有实际应用价值并易于实现。
-
我们在多种双曲模型上进行了广泛的实验,证明了我们提出的方法的有效性。
2 背景知识
2.1 黎曼几何与双曲空间(RiemannianGeometry and Hyperbolic Space)
黎曼几何
一个具有
d
d
d维的黎曼流形
M
\mathcal{M}
M是一个具有度量张量
g
g
g的拓扑空间,记作
(
M
,
g
)
(\mathcal{M},g)
(M,g)。一些重要的概念有:
- 在流形 M \mathcal{M} M中的任意点 x x x处,流形可以通过一个局部线性空间来局部逼近,该空间称为切空间 T x M \mathcal{T}_\mathbf{x}\mathcal{M} TxM,它与 R d \mathbb{R}^d Rd等距的。
- 流形上两点之间的最短路径称为测地线,其长度被称为诱导距离 d M d_{\mathcal{M}} dM。
- 在超曲面空间 (HDO) 中,节点到原点的距离可以理解为其对应的诱导超曲面范数。
- 为了将切向量投影到流形上,使用指数映射 exp x \exp_{\mathbf{x}} expx,而其逆函数被称为对数映射 log x \log_{\mathbf{x}} logx。
- 平行运输 P x → y P_{\mathbf{x}\to\mathbf{y}} Px→y,它允许将几何数据沿着唯一的测地线从 x x x 运输到 y y y ,同时保持度量张量不变。
双曲空间
双曲空间指的是具有常负曲率的黎曼流形,其坐标可以通过不同的等距模型来表示。在机器学习和深度学习领域,Poincaré 球模型和洛伦兹模型是广泛研究的模型。
一个
d
d
d 维的 Poincaré 球模型,其具有常负曲率
κ
(
κ
<
0
)
\kappa(\kappa<0)
κ(κ<0),定义为黎曼流形
(
B
κ
d
,
g
B
κ
)
\left( \mathcal{B}_\kappa^d, g_\mathcal{B}^\kappa \right)
(Bκd,gBκ)
- B κ d = { x ∈ R d ∣ ∥ x ∥ 2 < − 1 / κ } \mathcal{B}_\kappa^{d} = \{ \mathbf{x} \in \mathbb{R}^d \mid \|\mathbf{x}\|^2 < -1/\kappa \} Bκd={x∈Rd∣∥x∥2<−1/κ}
- 度量张量为 g B κ = ( λ x κ ) 2 I d g_\mathcal{B}^\kappa = (\lambda_\mathbf{x}^\kappa)^2 {\mathbf{I}}_d gBκ=(λxκ)2Id,其中 I d \mathbf{I}_d Id 是 d d d 维的单位矩阵。
- B κ d \mathcal{B}_\kappa^d Bκd 是半径为 ( − κ ) − 1 2 (-\kappa)^{-\frac12} (−κ)−21 的 d d d 维开球,而 λ x κ = 2 ( 1 + κ ∥ x ∥ 2 2 ) − 1 \lambda_\mathbf{x}^\kappa = 2(1 + \kappa \|\mathbf{x}\|_2^2)^{-1} λxκ=2(1+κ∥x∥22)−1 是共形因子。
洛伦兹模型
洛伦兹模型是另一个流行的双曲空间模型。在这个模型中,空间被看作是 ( d + 1 ) (d+1) (d+1) 维闵可夫斯基空间中双叶双曲面的其中一片。
一个具有常负曲率 κ ( κ < 0 ) \kappa(\kappa<0) κ(κ<0) 的 d d d 维洛伦兹模型(也称为双曲面模型)定义为黎曼流形 ( L κ d , g L κ ) (\mathcal{L}_\kappa^d, g_\mathcal{L}^\kappa) (Lκd,gLκ)
- 其中 L κ d = { x ∈ R d + 1 ∣ ⟨ x , x ⟩ L = 1 / κ } \mathcal{L}_\kappa^d = \{ \mathbf{x} \in \mathbb{R}^{d+1} \mid \langle \mathbf{x}, \mathbf{x} \rangle_{\mathcal{L}} = 1/\kappa \} Lκd={x∈Rd+1∣⟨x,x⟩L=1/κ}
- 度量张量为 g L κ = diag ( [ − 1 , 1 , ⋯ , 1 ] ) g_{\mathcal{L}}^\kappa = \text{diag}([-1, 1, \cdots, 1]) gLκ=diag([−1,1,⋯,1])。
需要注意的是,研究适用于 Poincaré 球模型和洛伦兹模型,为了简化,统一使用符号 H \mathcal{H} H。有关双曲公式,例如:指数映射 exp x κ \exp_{\mathbf{x}}^\kappa expxκ、对数映射 log x κ \log_{\mathbf{x}}^{\kappa} logxκ、双曲距离 d H d_{\mathcal{H}} dH 和平行运输 P o → x κ P_{\mathbf{o}\to\mathbf{x}}^{\kappa} Po→xκ 等。
2.2 双曲浅层模型
双曲浅层模型将实体编码到双曲空间中,并利用相对距离或相似性作为推断它们排序的手段。例如,、将数据嵌入到 Poincaré 球模型和洛伦兹模型中,通过优化以下目标来学习嵌入:
max x ∈ H d ∑ ( i , j ) ∈ E log exp ( − d H ( x i , x j ) ) ∑ j ′ ∈ N e g ( i ) exp ( − d H ( x i , x j ′ ) ) , ( 1 ) \max_{\mathbf{x} \in \mathcal{H}^d}\sum_{(i,j)\in E}\log\frac{\exp\left(-d_\mathcal{H}(\mathbf{x}_i,\mathbf{x}_j)\right)}{\sum_{j' \in Neg(i)}\exp\left(-d_\mathcal{H}(\mathbf{x}_i,\mathbf{x}_{j'})\right)}, (1) x∈Hdmax(i,j)∈E∑log∑j′∈Neg(i)exp(−dH(xi,xj′))exp(−dH(xi,xj)),(1)
- E E E 是由链接或相关对象对组成的集合
- N e g ( i ) = { j ∣ ( i , j ) ∉ E } ∪ { i } Neg(i) = \{j | (i,j) \notin E\} \cup \{i\} Neg(i)={j∣(i,j)∈/E}∪{i} 是 i i i 的负例集合
- x ∈ H d \mathbf{x} \in \mathcal{H}^d x∈Hd 是可训练的节点嵌入( x i \mathbf{x}_i xi 表示特定的对象 i i i)
- d H d_{\mathcal{H}} dH 是双曲距离。
- 优化目标鼓励原始数据中相连或相关的对象对具有较小的双曲距离。
2.3 双曲神经网络(HNNs)
HNN 的基本架构包括几个组件:
- 多项式逻辑回归(MLR)
- 全连接(FC)层
- 递归神经网络(RNNs)。
为了简洁起见,本研究主要集中在核心模块——即 FC 层。相应的双曲 FC 由线性变换和非线性激活组成。双曲线性变换首先进行矩阵乘法,然后是偏置平移。通常,这一过程可以在原点的切空间中实现。
给定一个双曲点 x ∈ H d \mathbf{x} \in \mathcal{H}^d x∈Hd,首先通过对数映射将其投影到原点的切空间 T o H d \mathcal{T}_{\mathrm{o}}\mathcal{H}^{d} ToHd,然后与权重矩阵 W ∈ R d ′ × d \mathbf{W} \in \mathbb{R}^{d^{\prime} \times d} W∈Rd′×d 相乘。双曲矩阵乘法定义为: W ⊗ κ x : = exp o κ ( W log o κ ( x ) ) \mathbf{W}\otimes^\kappa\mathbf{x} := \exp_{\mathbf{o}}^\kappa(\mathbf{W}\log_{\mathbf{o}}^\kappa(\mathbf{x})) W⊗κx:=expoκ(Wlogoκ(x))
- log o κ ( x ) ) \log_{\mathbf{o}}^\kappa(\mathbf{x})) logoκ(x))将特征从双曲空间转到切向量空间
- exp o κ \exp_{\mathbf{o}}^\kappa expoκ将特征从切向量空间空间转到双曲空间
对于偏置的加法,我们使用一个位于 T o H d \mathcal{T}_\mathrm{o}\mathcal{H}^d ToHd 的偏置 b \mathbf{b} b,并将其通过平行传输到感兴趣的双曲点,然后映射到流形上,定义为: x ⊕ κ b : = exp x κ ( P o → x κ ( b ) ) \mathbf{x} \oplus^\kappa \mathbf{b} := \exp_{\mathbf{x}}^\kappa(P_{\mathbf{o} \to \mathbf{x}}^\kappa(\mathbf{b})) x⊕κb:=expxκ(Po→xκ(b))
非线性激活也在切空间中实现,为简便起见,我们使用双曲原点,其定义为: σ H κ 1 , κ 2 ( x ) : = exp o κ 1 ( σ ( log o κ 2 ( x ) ) ) \sigma_{\mathcal{H}}^{\kappa_1, \kappa_2}(\mathbf{x}) := \exp_{\mathbf{o}}^{\kappa_1} \left( \sigma(\log_{\mathbf{o}}^{\kappa_2}(\mathbf{x})) \right) σHκ1,κ2(x):=expoκ1(σ(logoκ2(x)))
最后,给定
x
∈
H
d
\mathbf{x} \in \mathcal{H}^d
x∈Hd,第
ℓ
\ell
ℓ 层双曲神经网络的公式为:
x
ℓ
=
σ
H
κ
ℓ
,
κ
ℓ
−
1
(
W
⊗
κ
ℓ
−
1
x
ℓ
−
1
)
⊕
κ
ℓ
−
1
b
,
(
2
)
\mathbf{x}^{\ell} = \sigma_{\mathcal{H}}^{\kappa_{\ell}, \kappa_{\ell-1}} (\mathbf{W} \otimes^{\kappa_{\ell-1}} \mathbf{x}^{\ell-1}) \oplus^{\kappa_{\ell-1}} \mathbf{b},(2)
xℓ=σHκℓ,κℓ−1(W⊗κℓ−1xℓ−1)⊕κℓ−1b,(2)
- κ ℓ \kappa_{\ell} κℓ 和 κ ℓ − 1 \kappa_{\ell-1} κℓ−1 分别是第 ℓ \ell ℓ 层和第 ℓ − 1 \ell-1 ℓ−1 层的曲率。
2.4 双曲图卷积神经网络(HGCNs)
双曲图卷积神经网络(HGCNs)的核心是执行双曲空间内的图卷积。HGNNs 使用消息传递机制,包括线性变换、邻居聚合和非线性激活。
与方程(2)中给出的HNNs相比,HGCN 层多了一个邻居聚合步骤。设 j ∈ N ( i ) j \in \mathcal{N}(i) j∈N(i) 为节点 i i i 的邻居(包括自环),双曲邻居聚合定义为:
A G G κ ( x i ) : = exp x r κ ( ∑ j ∈ N ( i ) a ~ i j log x r κ ( x j ) ) \mathrm{AGG}^{\kappa}(\mathbf{x}_{i}):=\exp_{\mathbf{x}_{r}}^{\kappa}\left(\sum_{j\in\mathcal{N}(i)}\tilde{a}_{ij}\log_{\mathbf{x}_{r}}^{\kappa}(\mathbf{x}_{j})\right) AGGκ(xi):=expxrκ j∈N(i)∑a~ijlogxrκ(xj)
其中 x r \mathbf{x}_r xr 是双曲空间中的参考点,本研究中为简便起见将其设置为原点, a ~ i j \tilde{a}_{ij} a~ij 是归一化的边权,计算方法可以通过基于注意力的方法:
a ~ i j = Softmax j ∈ N ( i ) ( MLP ( log o κ ( x i ) ∥ log o κ ( x j ) ) ) \tilde{a}_{ij} = \text{Softmax}_{j \in \mathcal{N}(i)}(\text{MLP}(\log_{\mathbf{o}}^{\kappa}(\mathbf{x}_i) \| \log_{\mathbf{o}}^{\kappa}(\mathbf{x}_j))) a~ij=Softmaxj∈N(i)(MLP(logoκ(xi)∥logoκ(xj)))
或者通过对称归一化拉普拉斯矩阵:
a ~ i j = 1 d ~ i d ~ j , \tilde{a}_{ij} = \frac{1}{\sqrt{\tilde{d}_i \tilde{d}_j}}, a~ij=d~id~j1,
- 其中 d v d_v dv 表示节点 v v v 的度数(包括自环)。
然后,单个 HGNN 层的公式为:
x
i
ℓ
=
σ
H
κ
ℓ
−
1
,
κ
ℓ
(
h
~
i
ℓ
)
,
h
~
i
ℓ
=
A
G
G
κ
ℓ
−
1
(
h
i
ℓ
)
,
(
3
)
h
i
ℓ
=
(
W
ℓ
⊗
κ
ℓ
−
1
x
i
ℓ
−
1
)
⊕
κ
ℓ
−
1
b
ℓ
.
\begin{aligned} & \mathbf{x}_{i}^{\ell}=\sigma_{\mathcal{H}}^{\kappa_{\ell-1},\kappa_{\ell}}(\tilde{\mathbf{h}}_{i}^{\ell}), \\ & \tilde{\mathbf{h}}_{i}^{\ell}=\mathrm{AGG}^{\kappa_{\ell-1}}(\mathbf{h}_{i}^{\ell}), & \mathrm{(3)} \\ & \mathbf{h}_i^\ell=(\mathbf{W}^\ell\otimes^{\kappa_{\ell-1}}\mathbf{x}_i^{\ell-1})\oplus^{\kappa_{\ell-1}}\mathbf{b}^\ell. \end{aligned}
xiℓ=σHκℓ−1,κℓ(h~iℓ),h~iℓ=AGGκℓ−1(hiℓ),hiℓ=(Wℓ⊗κℓ−1xiℓ−1)⊕κℓ−1bℓ.(3)
3 当前存在问题
3.1 Hyperbolic Distance to Origin (HDO)
从点 x \mathbf{x} x 到原点 o \mathbf{o} o 的双曲距离(HDO),也称为诱导的双曲范数, d H ( x , o ) d_{\mathcal{H}}(\mathbf{x}, \mathbf{o}) dH(x,o)。
目前已在多个领域中得到了广泛应用,特别是在阐明嵌入层级结构的复杂性方面。
- 在 WordNet 4 ^4 4 嵌入中,通过嵌入范数的差异来定义一个得分函数,用于评估 Poincaré 嵌入在表示语义关系方面的有效性。
- 在图像嵌入中,将 HDO 作为不确定性量化指标,并发现难以分类的图像被嵌入到双曲空间的原点附近,而易于分类的图像则被放置在 Poincaré 边界附近。难以分类的图像通常包含来自不同类别的模式,这些模式与层级中的高级位置相关。而易于分类的图像则表现出特定的模式,这些模式与层级中的低级位置相关。
- 利用 HDO 分析了双曲用户-物品嵌入与流行度的对齐情况。分析结果表明,较小的 HDO 值表示较高的流行度水平。一个物品的流行度越高,意味着该物品被大量用户偏好,最受欢迎的物品通常作为网络的中心或树的根节点。
在一个 k k k-正则树中,层级 r r r 上的节点数量呈指数增长,为 ( k + 1 ) k r − 1 (k+1)k^{r-1} (k+1)kr−1,且层级小于或等于 r r r 的节点数量也呈类似的趋势,为 ( k + 1 ) k r − 2 k − 1 \frac{(k+1)k^r - 2}{k-1} k−1(k+1)kr−2。这意味着节点的数量随着距离树根的增加而增加。
- 在双曲空间中,圆盘的面积也随着距离双曲原点的增加而呈指数扩展。因此,战略性地将树的第 r r r 层节点放置在距离双曲原点的距离 R R R (其中 R R R 与 r r r 成正比)上,可以得到一个捕捉树状结构的层次化嵌入。
3.2 存在的问题
由于图数据集缺乏重要的几何信息,如根节点标签、层级信息和叶节点,因此合成了两个纯树形数据集。
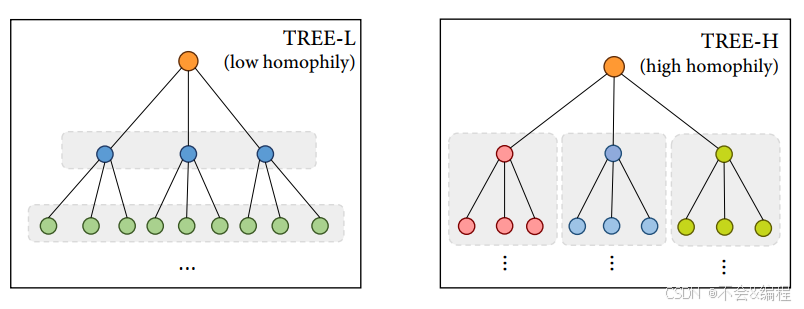
两个纯树形数据集具有不同同质性(homophily)程度的树形结构:TREE-H(同质性率为0.998)和TREE-L(同质性率为0.018)。
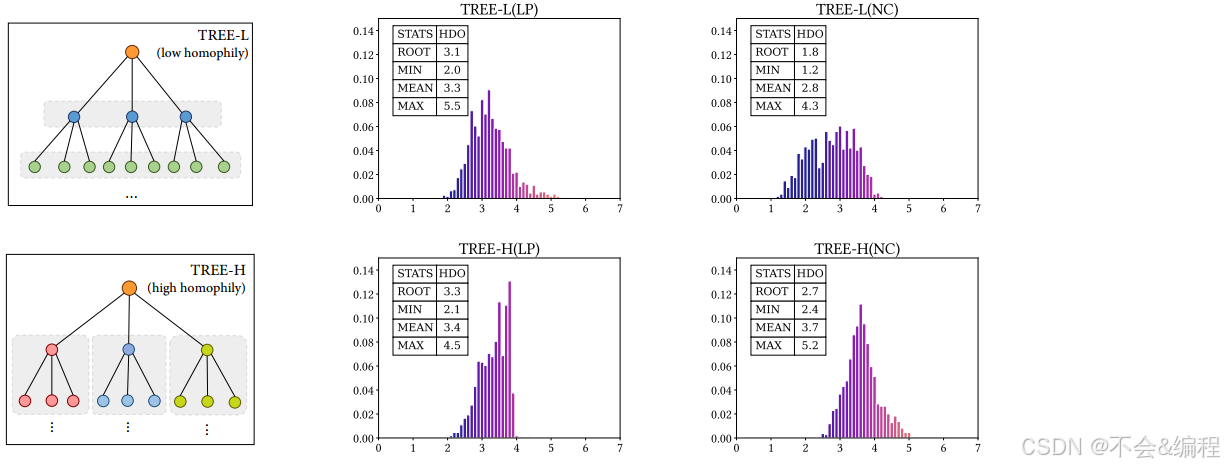
我们对HGCN在节点分类和链路预测任务中的表现进行了实验评估,并展示了最终嵌入层中节点状态的HDO分布,如图2所示。
- 合成的TREE-L/H结构示意图(第一列)
- HGCN在链路预测(LP)任务(第二列)中对应的HDO分布。
- HGCN在节点分类(NC)任务(第三列)中对应的HDO分布。
从实验结果中可以观察到: - 在这两种情况下,根节点与最小HDO值(参见MIN和ROOT值)之间存在较大差异。例如,在链路预测任务中,TREE-L和TREE-H的根节点ROOT值分别为3.1和3.3,而最小值MIN分别为2.0和2.1。
- HDO的分布呈现出更加正态的模式。
- 在树形结构中,叶节点占据了大多数,并且预计会位于离原点更远的地方,遵循幂律分布。
- 节点并未完全扩展,这可以从分布的形状以及最小、均值和最大HDO之间的差距推断出来。
双曲空间呈指数扩展,远离原点的区域显著更广阔,更能容纳更多节点。但上述的实验表明:
- 根节点没有被优化为位于或接近最高层级,这可能导致层次结构不准确。(HDO值太大)
- 学习到的嵌入的HDO呈正态分布,这不足以捕捉树状结构。(正态分布没有层次性)
- 整体嵌入没有最大程度地散开,表明模型未能充分利用双曲空间的扩展特性。
4 HIE模型
4.1 算法 双曲信息嵌入 (HIE)
双曲信息嵌入 (HIE)
-
输入:
- (i) 输入数据 X \mathcal{X} X,可以是 n n n 个一般的输入样本 X = { x 1 , ⋯ , x n } \mathcal{X}=\{\mathbf{x}_1, \cdots, \mathbf{x}_n\} X={x1,⋯,xn},或者是包含邻接矩阵的图中 n n n 个节点,即 X = { x 1 , ⋯ , x n , A } \mathcal{X}=\{\mathbf{x}_1, \cdots, \mathbf{x}_n, \mathbf{A}\} X={x1,⋯,xn,A}; x i \mathbf{x}_i xi 可以是随机采样的且可训练的,或者是预定义的。
- (ii) 学习模型 F \mathcal{F} F,可选择地由 W \mathbf{W} W 参数化。
- (iii) 超参数 λ > 0 \lambda > 0 λ>0。
-
输出: n n n 个对象的嵌入和最优的 W \mathbf{W} W。
-
初始化F的输入数据 χ \chi χ和可学习权重 W \mathbf{W} W(可选)。
-
计算嵌入 Z ← F ( [ W ] , X ) \mathbf{Z} \leftarrow \mathcal{F}([\mathbf{W}], \mathcal{X}) Z←F([W],X);
-
如果是部分根对齐:
- 计算特定任务的损失: L t a s k L_\mathrm{task} Ltask;
- 计算根对齐的嵌入 Z ˉ \bar{\mathbf{Z}} Zˉ;
- 计算到原点的双曲距离损失: L h y p L_\mathrm{hyp} Lhyp;
- 使用总体损失函数进行优化: L t a s k + λ L h y p L_\mathrm{task} + \lambda L_\mathrm{hyp} Ltask+λLhyp;
- 返回 Z , W \mathbf{Z}, \mathbf{W} Z,W;
-
end if;
-
如果是全部根对齐:
- 计算根对齐嵌入 Z ˉ \bar{\mathbf{Z}} Zˉ;
- 计算到原点的双曲距离损失: L h y p L_\mathrm{hyp} Lhyp;
- 计算特定任务的损失: L t a s k L_\mathrm{task} Ltask;
- 使用总体损失函数进行优化: L t a s k + λ L h y p L_{\mathrm{task}} + \lambda L_{\mathrm{hyp}} Ltask+λLhyp;
- 返回 Z ˉ , W \bar{\mathbf{Z}}, \mathbf{W} Zˉ,W;
-
end if;
所提出的方法可以通过两种方式实现:
- 一种是硬操作,替换所有原始嵌入。对所有节点的嵌入都进行根对齐。即,将图中的所有节点的嵌入朝着双曲空间的原点对齐。
- 另一种方法是通过在 L h y p L_\mathrm{hyp} Lhyp损失函数中部分实现它来生成所需的更新梯度。即根对齐操作仅应用于那些特定节点的嵌入,通常是与任务相关的节点或部分嵌入。
4.2 双曲空间HIE
为了解决上述问题,提出了HIE算法。
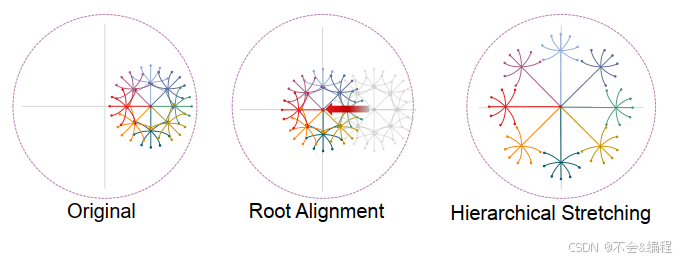
如下图所示,HIE的基本思想示意图,可以分解为两个关键步骤:
- 根对齐。即根节点并将其对齐到双曲空间的原点
- 层次感知,拉伸。即根据每个节点的层次信息,将其优化到远离原点的位置。
但是实现上述目标存在挑战:
- 定义和定位根节点:许多指标,如中心性,可以描述节点在图中的作用。然而,这些方法仅依赖于图的拓扑结构,忽略了节点的特征。此外,当处理大规模图时,一些指标的计算开销较大。而且,树状数据集通常包含多个子树或根节点。
- 高效获取层次信息并引导层次学习:在现实世界的场景中,这种层次信息很少现成可得,并且在大规模数据集上标注这些信息是人工完成的。
4.2.1 双曲嵌入中心(HC)
首先解决第一个挑战,解决方案是:利用双曲嵌入中心(HC)作为根节点,并将其与双曲空间的原点进行对齐。
HC的定理如下:
定理1. 给定图 G = ( V , E ) G = (V, E) G=(V,E)中的节点嵌入 z ∈ H d z ∈ H^d z∈Hd。双曲嵌入中心 z c ∈ H d z_c ∈ H^d zc∈Hd是和所有节点的加权双曲距离平方和的最小化问题的解,表达式如下: z c = min z a ∈ H d , κ ∑ i ∈ V v i d H 2 ( z i , z a ) , \mathbf{z}_c=\min_{\mathbf{z}_a\in\mathcal{H}^{d,\kappa}}\sum_{i\in V}v_id_\mathcal{H}^2(\mathbf{z}_i,\mathbf{z}_a), zc=za∈Hd,κmini∈V∑vidH2(zi,za),
- z a z_a za 是流形中的任意一点,嵌入中心包括 Poincaré 球模型中的莫比乌斯圆心和洛伦兹模型中的加权质心。
HC是通过特定流形的方法计算的,并作为最优解来最小化与所有节点的平方距离和。这符合规则树中根结点的特性,即是与其他结点的距离总和最小的结点。
HC的优势如下:
- 计算 HC 相对简单,计算成本为 O ( ∣ V ∣ ) O(|V|) O(∣V∣),或者在利用 GPU 进行并行计算时为 O ( 1 ) O(1) O(1)。
- HC 来源于双曲嵌入,能够编码结构和特征信息。它有效处理多个根节点的情况,因为 HC 总是代表一个独特的点,可以看作是连接所有子树的超节点。
- HC 可以根据下游任务在学习过程中自适应调整。
令 Z \mathbf{Z} Z 为最终层嵌入矩阵,其中包含 n n n 个双曲节点向量 ( z 1 , ⋯ , z i , ⋯ , z n ) (\mathbf{z}_1, \cdots, \mathbf{z}_i, \cdots, \mathbf{z}_n) (z1,⋯,zi,⋯,zn),其中 z i ∈ H κ d \mathbf{z}_i \in \mathcal{H}_\kappa^d zi∈Hκd,并令 v i v_i vi 表示分配给 z i \mathbf{z}_i zi 的权重。函数 f c f_c fc 用于计算加权中心, z c \mathbf{z}_c zc 表示该中心,则计算公式为: z c = f c ( { z i , v i ∣ i ∈ V } ) \mathbf{z}_c = f_c(\{\mathbf{z}_i, v_i | i \in V\}) zc=fc({zi,vi∣i∈V})
- f c f_c fc 可在附录查看
接下来,我们采用根对齐策略,公式如下:
z
ˉ
=
z
⊕
κ
(
−
z
c
)
,
(root alignment)(4)
\bar{\mathbf{z}}=\mathbf{z}\oplus_\kappa(-\mathbf{z}_c),\quad\text{(root alignment)(4)}
zˉ=z⊕κ(−zc),(root alignment)(4)
- ⊕ κ \oplus_\kappa ⊕κ 表示双曲加法操作,具体操作可在附录查看
4.2.2 层次伸缩方法
为了解决第二个挑战,利用HDO对节点进行层次扩展。即,将双曲嵌入中心(即根节点)与双曲空间的原点对齐,之后HDO可以更准确地反映节点相对于根节点的相对距离,从而指示其层次级别,公式如下:
z
h
d
o
=
1
∣
V
∣
∑
i
∈
V
w
i
d
H
(
z
ˉ
i
,
o
)
,
(HDO computation)(5)
z_{\mathrm{hdo}}=\frac{1}{|V|}\sum_{i\in V}w_id_{\mathcal{H}}(\bar{\mathbf{z}}_i,\mathbf{o}),\quad\text{(HDO computation)(5)}
zhdo=∣V∣1i∈V∑widH(zˉi,o),(HDO computation)(5)
- w i w_i wi 表示双曲空间中的节点级别,它是通过 HDO 得到的 ( w i : = f ( d H ( z ˉ i , o ) ) ) (w_i := f(d_{\mathcal{H}}(\bar{\mathbf{z}}_i, \mathbf{o}))) (wi:=f(dH(zˉi,o))),其中 f f f 是单调递增函数,如线性函数、tanh、sigmoid 等。
- 越靠近原点, w i w_i wi 越小
它被整合到损失函数中,如下:
L
h
y
p
=
σ
(
−
z
h
d
o
)
,
(
stretching
)
(
6
)
L_{\mathrm{hyp}}=\sigma(-z_{\mathrm{hdo}}),\quad(\text{stretching})\quad(6)
Lhyp=σ(−zhdo),(stretching)(6)
- 通过最小化 L h y p L_\mathrm{hyp} Lhyp 来实现拉伸,其中使用了单调递增函数 σ \sigma σ(线性函数、tanh、exp 等)。
- 当 z h d o z_{\mathrm{hdo}} zhdo越大,说明有很多节点已经远离双曲中心,此时。损失函数就越小
通过最小化上述损失函数,可以使:
- 靠近原点的高级节点将被赋予较小的权重,从而避免它们被推开。
- 远离原点的低级节点将被赋予较大的权重,以便它们能够到达正确的位置。
4.2.3 切空间HIE
在双曲学习领域,一种常见的方法是在双曲空间的原点的切空间中建模数据。因此,引入了对 HIE 模型的扩展,称为切空间版本 HIE
7
^7
7。假设我们有切向嵌入
z
T
z^{T}
zT,就得到了方程 (7) (8) (9)。
z
ˉ
T
=
z
T
−
z
c
T
(root alignment) (7)
z
h
d
o
T
:
=
1
∣
V
∣
∑
i
∈
V
w
i
d
(
z
ˉ
i
T
,
o
T
)
(HDO computation) (8)
L
h
y
p
=
σ
(
−
z
h
d
o
T
)
(stretching) (9)
\bar{\mathbf{z}}^T=\mathbf{z}^T-\mathbf{z}_c^T\quad\text{(root alignment)~~(7)} \\ z_{\mathrm{hdo}}^{\mathcal{T}}:=\frac{1}{|V|}\sum_{i\in V}w_{i}d(\bar{\mathbf{z}}_{i}^{\mathcal{T}},\mathbf{o}^{\mathcal{T}})\quad\text{(HDO computation) ~~(8)} \\ L_{\mathrm{hyp}}=\sigma(-z_{\mathrm{hdo}}^{\mathcal{T}})\quad\text{(stretching) ~~ (9)}
zˉT=zT−zcT(root alignment) (7)zhdoT:=∣V∣1i∈V∑wid(zˉiT,oT)(HDO computation) (8)Lhyp=σ(−zhdoT)(stretching) (9)
- z c T : = 1 ∣ V ∣ ∑ i ∈ V z i T \mathbf{z}_c^T := \frac{1}{|V|}\sum_{i \in V} \mathbf{z}_i^T zcT:=∣V∣1∑i∈VziT 表示切向嵌入的中心。
- w i w_i wi 来源于 d ( z ˉ i , o ) d(\bar{\mathbf{z}}_i, \mathbf{o}) d(zˉi,o),为了简化,我们使用恒等函数,这表示欧几里得距离。符号 σ \sigma σ 表示单调递增函数,如线性函数、tanh、sigmoid 等。
双曲切向嵌入中心的计算方式如下:
定理 2. 给定图 G = { V , E } G = \{ V, E\} G={V,E} 的节点嵌入 z ∈ H d z \in \mathcal{H}^d z∈Hd,双曲切向嵌入中心 z c T ∈ T o H d \mathbf{z}_c^{T} \in \mathcal{T}_{\mathbf{o}} \mathcal{H}^d zcT∈ToHd 是加权平方距离和最小化问题的解:所有节点在切空间 T o H d T_{\mathbf{o}} \mathcal{H}^d ToHd 中的距离之和,表示为:
z c T = min z a T ∈ T o H d , κ ∑ i ∈ V v i d 2 ( z i T , z a T ) \mathbf{z}_c^{\mathcal{T}} = \min_{\mathbf{z}_a^{\mathcal{T}} \in \mathcal{T}_{\mathbf{o}} \mathcal{H}^{d, \kappa}} \sum_{i \in V} v_i d^2(\mathbf{z}_i^{\mathcal{T}}, \mathbf{z}_a^{\mathcal{T}}) zcT=zaT∈ToHd,κmini∈V∑vid2(ziT,zaT)
- 其中 z a T z_a^T zaT 是流形切空间中的任意一点。
5 附录
A.黎曼几何
在本节中,将介绍文中提到的概念的详细内容,即黎曼几何 ( M , g ) (\mathcal{M}, g) (M,g) 中的测地线、距离函数、映射和平行运输,并总结研究中使用的双曲空间公式。
测地线和距离函数
对于一条曲线 γ : [ α , β ] → M \gamma:[\alpha, \beta] \to \mathcal{M} γ:[α,β]→M,称其为测地线(geodesic),其长度定义为 L ( γ ) = ∫ α β ∥ γ ′ ( t ) ∥ g d t L(\gamma) = \int_{\alpha}^{\beta} \| \gamma'(t) \|_g dt L(γ)=∫αβ∥γ′(t)∥gdt。
点 u , v ∈ M \mathbf{u}, \mathbf{v} \in \mathcal{M} u,v∈M 之间的距离由该公式给出: d M ( u , v ) = inf L ( γ ) d_\mathcal{M}(\mathbf{u}, \mathbf{v}) = \inf L(\gamma) dM(u,v)=infL(γ),其中 γ \gamma γ 是一条满足 γ ( α ) = u \gamma(\alpha) = \mathbf{u} γ(α)=u 和 γ ( β ) = v \gamma(\beta) = \mathbf{v} γ(β)=v 的曲线。
映射和平行运输
假设流形是光滑的,即映射是微分同胚的,映射定义了流形与切空间之间的投影。
对于一个点 x ∈ M \mathbf{x} \in \mathcal{M} x∈M 和一个向量 v ∈ T x M \mathbf{v} \in \mathcal{T}_{\mathbf{x}} \mathcal{M} v∈TxM,存在一条唯一的测地线 γ : [ 0 , 1 ] → M \gamma:[0, 1] \to \mathcal{M} γ:[0,1]→M,其中 γ ( 0 ) = x \gamma(0) = \mathbf{x} γ(0)=x 且 γ ′ ( 0 ) = v \gamma'(0) = \mathbf{v} γ′(0)=v。
指数映射 exp x : T x M → M \exp_{\mathbf{x}} : \mathcal{T}_{\mathbf{x}} \mathcal{M} \to \mathcal{M} expx:TxM→M 定义为 exp x ( v ) = γ ( 1 ) \exp_\mathbf{x}(\mathbf{v}) = \gamma(1) expx(v)=γ(1),而对数映射 log x : M → T x M \log_\mathbf{x} : \mathcal{M} \to \mathcal{T_\mathbf{x}} \mathcal{M} logx:M→TxM 是 exp x \exp_\mathbf{x} expx 的逆映射。
平行运输 P T x → y : T x M → T y M PT_{\mathbf{x} \to \mathbf{y}} : \mathcal{T_{\mathbf{x}}} \mathcal{M} \to \mathcal{T_{\mathbf{y}}} \mathcal{M} PTx→y:TxM→TyM 实现了从点 x \mathbf{x} x 到点 y \mathbf{y} y 的运输,并沿着唯一的测地线保持度量张量不变。
双曲模型
具有不同曲率的黎曼流形定义了不同的几何类型:
- 椭圆几何(正曲率)
- 欧几里得几何(零曲率)
- 双曲几何(负曲率)。
双曲几何是具有常数负截面曲率的黎曼流形。我们主要考虑两种广泛研究的双曲模型:庞加莱球模型和洛伦兹模型。
Möbius 加法与减法
令 ∥ . ∥ \|.\| ∥.∥ 为欧几里得范数, ⟨ . , . ⟩ L \langle.,.\rangle_\mathcal{L} ⟨.,.⟩L 表示闵可夫斯基内积。其中 ⊕ κ \oplus_\kappa ⊕κ 和 gyr [ . , . ] v [.,.]v [.,.]v 分别是 Möbius 加法和旋转算子(Ungar et al., 2007),其定义如下:
Möbius 加法:对于 x , y ∈ B κ n \mathbf{x}, \mathbf{y} \in \mathcal{B}_\kappa^n x,y∈Bκn,Möbius 加法定义为:
x ⊕ κ y = ( 1 − 2 κ ⟨ x , y ⟩ 2 − κ ∥ y ∥ 2 2 ) x + ( 1 + κ ∥ x ∥ 2 2 ) y 1 − 2 κ ⟨ x , y ⟩ 2 + κ 2 ∥ x ∥ 2 2 ∥ y ∥ 2 2 . \mathbf{x}\oplus_\kappa\mathbf{y}=\frac{\left(1-2\kappa\langle\mathbf{x},\mathbf{y}\rangle_2-\kappa\|\mathbf{y}\|_2^2\right)\mathbf{x}+\left(1+\kappa\|\mathbf{x}\|_2^2\right)\mathbf{y}}{1-2\kappa\langle\mathbf{x},\mathbf{y}\rangle_2+\kappa^2\|\mathbf{x}\|_2^2\|\mathbf{y}\|_2^2}. x⊕κy=1−2κ⟨x,y⟩2+κ2∥x∥22∥y∥22(1−2κ⟨x,y⟩2−κ∥y∥22)x+(1+κ∥x∥22)y.
- 诱导的 Möbius 减法 ⊖ κ \ominus_\kappa ⊖κ 定义为 x ⊖ κ y = x ⊕ κ ( − y ) \mathbf{x}\ominus_\kappa\mathbf{y} = \mathbf{x}\oplus_\kappa(-\mathbf{y}) x⊖κy=x⊕κ(−y)。
旋转算子的概念定义为:
gyr [ x , y ] v = ⊖ κ ( x ⊕ κ y ) ⊕ κ ( x ⊕ κ ( y ⊕ κ v ) ) . \text{gyr}[\mathbf{x}, \mathbf{y}]\mathbf{v} = \ominus_{\kappa}\left(\mathbf{x}\oplus_{\kappa}\mathbf{y}\right)\oplus_{\kappa}\left(\mathbf{x}\oplus_{\kappa}\left(\mathbf{y}\oplus_{\kappa}\mathbf{v}\right)\right). gyr[x,y]v=⊖κ(x⊕κy)⊕κ(x⊕κ(y⊕κv)).
如下表所示,庞加莱球模型和洛伦兹模型中的运算总结(
κ
<
0
\kappa < 0
κ<0)
B. 关于 TREE-L 和 TREE-H 的数据集构建
一个真实世界数据集的几何信息通常没有明确给出,而且该数据集通常也不是一个纯树结构,因此我们合成了两个树数据集,TREE-L 和 TREE-H,用于跟踪节点嵌入在双曲空间中的位置。
-
结构:TREE-L 和 TREE-H 都有相同的树结构,包含 8 层、1092 条边和 1093 个节点。除了叶子节点,每个节点都有 3 个子节点。
-
同质性差异:
-
TREE-H:具有高同质性。每个最大子树(共三个最大子树)中的节点有相同的标签。根节点为一个单独的类别,其余的节点分为 3 个类别。每个类别的节点特征是从高斯分布中生成的 32 维向量,均值和方差分别为:
- 类别 1(根节点):(0.0, 1.0)
- 类别 2: (1.0, 1.0)
- 类别 3: (2.0, 1.0)
- 类别 4: (3.0, 1.0)
-
TREE-L:具有较低的同质性。每一层的节点具有相同的标签。前四层节点被设置为同一类别,保证总共有四个类别。类别的特征生成方法和均值、方差与 TREE-H 相同。
-
如下图所示:
- 注意:使用相同的颜色来表示这两个树中的相同类。
一种度量图的同质性率 H m H_m Hm 的方法,定义为:
H m ( G ) = 1 ∣ V ∣ ∑ v ∈ V # Label ( v ′ s neighbors ) = = Label of v # v ′ s neighbors . H_m(G)=\frac{1}{|V|}\sum_{v\in V}\frac{\#\text{Label}(v'\text{s neighbors})==\text{Label of }v}{\#v'\text{s neighbors}}. Hm(G)=∣V∣1v∈V∑#v′s neighbors#Label(v′s neighbors)==Label of v.
然后,计算得到的 TREE-H 和 TREE-L 的同质性率 H m H_m Hm 分别为 0.998 和 0.018。
C. 双曲中点计算与对齐( f c f_c fc 和 ⊕ κ \oplus_\kappa ⊕κ)
设 Z Z Z 为最终层的嵌入矩阵,包含 n n n 个双曲节点向量 ( z 1 , ⋯ , z i , ⋯ , z n ) (\mathbf{z}_1, \cdots, \mathbf{z}_i, \cdots, \mathbf{z}_n) (z1,⋯,zi,⋯,zn),其中 z i ∈ H κ d \mathbf{z}_i \in \mathcal{H}_\kappa^d zi∈Hκd,并且设 v i ∈ R ( v i ≥ 0 v_i \in \mathbb{R} \left( v_i \geq 0 \right. vi∈R(vi≥0 且 ∑ i v i > 0 ) \sum_i v_i > 0) ∑ivi>0) 为 z i z_i zi 的权重,在本研究中将其设为 1。以下给出了双曲中心 z c z_c zc 的计算及对齐的详细信息。
庞加莱球模型
在庞加莱球模型中,中心,即莫比乌斯旋转中点,是在gyrovector space中计算的,计算公式为:
z c : = 1 2 ⊕ κ ( ∑ i = 1 n v i λ z i κ z i ∑ i = 1 n v i ( λ z i κ − 1 ) ) , \mathbf{z}_c := \frac{1}{2} \oplus_\kappa \left( \frac{\sum_{i=1}^n v_i \lambda_{\mathbf{z}_i}^\kappa \mathbf{z}_i}{\sum_{i=1}^n v_i \left( \lambda_{\mathbf{z}_i}^\kappa - 1 \right)} \right), zc:=21⊕κ(∑i=1nvi(λziκ−1)∑i=1nviλziκzi),
- 其中 λ z i κ = 2 1 + κ ∥ z i ∥ 2 2 \lambda_{\mathbf{z}_i}^\kappa = \frac{2}{1 + \kappa \|\mathbf{z}_i\|_2^2} λziκ=1+κ∥zi∥222。
根对齐操作与Poincare球模型中的加法有关,由附录A公式计算得出。
洛伦兹模型
在洛伦兹模型中,中心(也称为洛伦兹质心)通过以下公式计算:
z c : = 1 ∣ κ ∣ ∑ i = 1 n v i z i ∣ ∥ ∑ i = 1 n v i z i ∥ L ∣ , \mathbf{z}_c := \frac{1}{\sqrt{|\kappa|}}\frac{\sum_{i=1}^n v_i \mathbf{z}_i}{|\left\|\sum_{i=1}^n v_i \mathbf{z}_i \right\|_{\mathcal{L}}|}, zc:=∣κ∣1∣∥∑i=1nvizi∥L∣∑i=1nvizi,
根对齐操作公式为:
z i ⊕ κ ( z c ) : = exp z ˉ κ ( P T o → z ˉ ( log o κ ( z i ) ) ) . \mathbf{z}_i \oplus_\kappa (\mathbf{z}_c) := \exp_{\mathbf{\bar{z}}}^\kappa(PT_{\mathbf{o} \to \mathbf{\bar{z}}}(\log_\mathbf{o}^\kappa(\mathbf{z}_i))). zi⊕κ(zc):=expzˉκ(PTo→zˉ(logoκ(zi))).
切空间
在切空间中,首先将嵌入
Z
\mathbf{Z}
Z 投影到原点的切空间上,即
Z
T
=
log
o
κ
(
Z
T
)
\mathbf{Z}^T = \log_{\mathbf{o}}^\kappa(\mathbf{Z}^T)
ZT=logoκ(ZT)。然后,中心通过以下加权方式定义:
z c T : = ∑ i = 1 n v i z i T ∑ i = 1 n v i , \mathbf{z}_c^T := \frac{\sum_{i=1}^n v_i \mathbf{z}_i^\mathcal{T}}{\sum_{i=1}^n v_i}, zcT:=∑i=1nvi∑i=1nviziT,
根对齐如下:
z i T ⊕ κ ( z c ) : = z i T − z c T . \mathbf{z}_i^{\mathcal{T}} \oplus_\kappa (\mathbf{z}_c) := \mathbf{z}_i^{\mathcal{T}} - \mathbf{z}_c^{\mathcal{T}}. ziT⊕κ(zc):=ziT−zcT.
D. Graph Centrality
在图论和网络分析中,中心性指标反映它们在网络中的相对重要性和显著性。在这一部分,我们将介绍一些图中常见的中心性指标供参考。除非另有说明,这里提到的图假设为无向图。
Degree centrality
度中心性:通过计算与节点相连的边的数量来量化节点的中心性,这个数量通常被称为该节点的度数:
C
D
(
v
)
=
deg
(
v
)
.
C_D(v) = \deg(v).
CD(v)=deg(v).
- 度越高的结点在网络中的中心性越强,因此我们选择度越高的结点作为比较的根结点。
Betweenness centrality
一个节点的介数中心性是基于通过它的最短路径的数量。公式如下:
C B ( v ) = ∑ s ≠ v ≠ t ∈ V δ s t ( v ) δ s t , C_B(v) = \sum_{s \neq v \neq t \in V} \frac{\delta_{st}(v)}{\delta_{st}}, CB(v)=s=v=t∈V∑δstδst(v),
- δ s t \delta_{st} δst 表示从节点 s s s 到节点 t t t 的最短路径总数
- δ s t ( v ) \delta_{st}(v) δst(v) 表示经过节点 v v v 的最短路径数量。
closeness centrality
接近度中心性量化了节点与网络中所有其他节点之间的连接紧密程度。接近度中心性的核心概念是,如果一个节点到达另一个节点所需的平均链接数较少,那么该节点就是中心节点。它通过取节点与图中其他所有节点之间的最短路径距离之和的倒数来计算,公式为:
C C ( v ) = n − 1 ∑ u = 1 n − 1 d ( v , u ) , C_C(v) = \frac{n-1}{\sum_{u=1}^{n-1} d(v,u)}, CC(v)=∑u=1n−1d(v,u)n−1,
- d ( v , u ) d(v,u) d(v,u) 是节点 v v v 和节点 u u u 之间的最短路径距离, n − 1 n-1 n−1 是从节点 v v v 可达的节点数量。