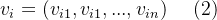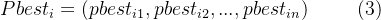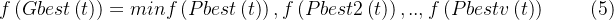粒子群算法(PSO)是由美国社会心理学家J.Kennedy和电器工程师R.Eberhart于1995年共同提出的。起源于对简单社会系统的模拟,因此它既保持了传统进化算法的群体智慧背景,同时又具有良好的优化性能。关注:人工智能与算法优化,回复“PSO”或“粒子群算法”获取源代码。
01 算法理论基础
PSO算法的基本思想受到许多对鸟类的群体行为进行建模与仿真研究结果的启发,最初设想是模拟鸟群觅食的过程。“如一群鸟随机分布在一个区域,且此区域中只有一块食物,但是所有的鸟都不知道这块食物具体方位,只知道自己当前位置距离食物还有多远”。找到食物最简单有效的方式就是搜索目前到食物最近鸟的周围区域。如果把食物当作最优点,而把鸟到食物的距离当作函数的适应度,那么鸟寻觅食物的过程就可以当作函数寻优的过程。由此受到启发,提出了PSO算法。
02 算法实现
PSO算法中没有进化算子,而是将每个个体看作搜索空间中一个没有重量和体积的微粒,并在搜索空间中以一定的速度飞行,该飞行速度由个体飞行经验和群体的飞行经验进行动态调整。
其中 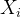

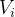

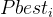
若 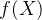

其中,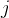



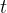
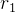
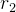
![[0,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIwJTJDMSU1RA%3D%3D)
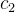
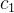
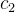
03 粒子群算法流程图
粒子群算法流程图,如下图所示:
图1 粒子群算法流程图
粒子群算法伪代码,如下
%%算法:粒子群优化算法(MATLAB)
FOR each particle i
FOR each dimension j
Initialize position x(i,j) randomly within permissible range
Initialize velocity v(i,j),randomly within permissible range
END FOR
END FOR
Iteration t =1
DO
FOR each particle i
Calculate fitness value
IF the fitness value is better than Gbest(t) in history
Set current fitness value as the Gbest(t)
END IF
END FOR
Choose the particle having the best fitness value as the Gbest(t)
FOR each particle i
FOR each dimension j
Calculate velocity according to the equation
Equation(6)
Update particle position according to the equation
Equation(7)
END FOR
END FOR
t =t+1
WHILE maximum iterations or minimum error criteria are not allained
END 04 参考文献
[1] Kennedy J, Eberhart R C. Particle Swarm Optimization[C]. IEEE Conference on Neural Networks, Piscataway, NJ: IEEE Service Center, 1995: 1942-1948.

![X_i=[x_{i1},x_{i2},...,x_{in}] \ \ \ \ \ \ \ \ \ \ (1)](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9YX2klM0QlNUJ4XyU3QmkxJTdEJTJDeF8lN0JpMiU3RCUyQy4uLiUyQ3hfJTdCaW4lN0QlNUQlMjAlNUMlMjAlNUMlMjAlNUMlMjAlNUMlMjAlNUMlMjAlNUMlMjAlNUMlMjAlNUMlMjAlNUMlMjAlNUMlMjAlMjgxJTI5)