有限差分方法解决一维波动问题:Python实现
1. 有限差分方法
有限差分方法是一种数值分析中的方法,主要用于解决微分方程。在连续函数的微分和积分中,我们通常使用微积分的方法。但在实际应用中,很多情况下我们无法得到函数的精确表达式,或者即使得到了,求解微分或积分也非常复杂。这时,我们就可以使用有限差分法。
我们导数的概念时知道,连续函数的导数其实是通过相邻离散点作差分然后取极限得到的,即:
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}
f′(x)=h→0limhf(x+h)−f(x)
解微分方程时,将所有的导数项用离散点处的差分来近似,这就是有限差分法的主要思想。
1.1. 一般步骤
有限差分方法的一般步骤包括:
- 离散化:
将偏微分方程中的自变量和因变量在计算区域内用离散的网格点表示,得到一个离散化模型。 - 差分近似:
利用差分运算近似代替偏微分方程中的导数,将偏微分方程转化为一组代数方程。常见的差分公式有:-
向前差分:
f ′ ( x ) ≈ f ( x + h ) − f ( x ) h f'(x) \approx \frac{f(x+h)-f(x)}{h} f′(x)≈hf(x+h)−f(x) -
向后差分:
f ′ ( x ) ≈ f ( x ) − f ( x − h ) h f'(x) \approx \frac{f(x)-f(x-h)}{h} f′(x)≈hf(x)−f(x−h) -
中心差分:
f ′ ( x ) ≈ f ( x + h ) − f ( x − h ) h f'(x) \approx \frac{f(x+h)-f(x-h)}{h} f′(x)≈hf(x+h)−f(x−h)
-
现在推导二阶导数的差分形式,首先对于二阶导数,由向后差分,有:
f
′
′
(
x
)
≈
f
′
(
x
)
−
f
′
(
x
−
h
)
h
f''(x) \approx \frac{f'(x)-f'(x-h)}{h}
f′′(x)≈hf′(x)−f′(x−h)
再将一阶导数使用向前差分:
f
′
′
(
x
)
≈
f
′
(
x
)
−
f
′
(
x
−
h
)
h
≈
f
(
x
+
h
)
−
f
(
x
)
h
−
f
(
x
)
−
f
(
x
−
h
)
h
h
≈
f
(
x
+
h
)
+
f
(
x
−
h
)
−
2
f
(
x
)
h
2
\begin{aligned} f''(x) &\approx \frac{f'(x)-f'(x-h)}{h} \\ &\approx \frac{ \frac{f(x+h)-f(x)}{h} - \frac{f(x)-f(x-h)}{h}}{h} \\ &\approx \frac{f(x+h)+f(x-h)-2f(x)}{h^2} \end{aligned}
f′′(x)≈hf′(x)−f′(x−h)≈hhf(x+h)−f(x)−hf(x)−f(x−h)≈h2f(x+h)+f(x−h)−2f(x)
这些公式均可通过对偏微分方程进行泰勒级数展开和差分近似得到,可自行推导。
-
边界条件:
根据实际问题的边界条件,确定网格中的边界值,作为差分方程求解的初始条件。 -
求解差分方程:
利用迭代法、直接法、Krylov 子空间法和前置处理方法等,求解离散化后的代数方程组,得到数值解。-
迭代法: 包括 Jacobi 迭代法、Gauss-Seidel 迭代法、SOR 迭代法等,这种方法的优点是计算速度快,特别适用于求解大型稀疏方程组,但精度可能受到迭代次数和初始猜测等因素的影响。
-
直接法: 包括高斯消元法、LU 分解法、cholesky 分解法等,这种方法的优点是精度高,但在求解大型稠密方程组时计算量较大。
-
Krylov 子空间法: Krylov 子空间法是一类基于迭代的快速线性方程组求解方法,例如 CG 方法、GMRES 方法、BiCGSTAB 方法等。这种方法的优点是计算速度快,而且对于大型稀疏方程组,其计算复杂度随着问题规模的增加而增长较慢。
-
前置处理方法: 前置处理方法是指在求解方程组之前,对方程组进行变换、重组或加权等操作,以提高求解速度和精度。常用的前置处理方法包括代数多重网格法、预处理共轭梯度法 PCG 等。
-
2. 琴弦振动问题
一维波动方程:
∂
2
u
∂
t
2
−
c
2
∂
2
u
∂
x
2
=
0
,
x
∈
[
0
,
1
]
,
t
∈
[
0
,
1
]
\frac{\partial^2u}{\partial t^2} - c^2 \frac{\partial^2u}{\partial x^2} = 0, x\in[0, 1], t\in[0, 1]
∂t2∂2u−c2∂x2∂2u=0,x∈[0,1],t∈[0,1]
初始条件:
u
(
x
,
0
)
=
u
t
(
x
,
0
)
=
s
i
n
(
π
x
)
u(x, 0) = u_t(x,0) = sin(\pi x)
u(x,0)=ut(x,0)=sin(πx)
边界条件:
u
(
0
,
t
)
=
0
,
u
(
1
,
t
)
=
0
u(0, t) = 0, u(1, t) = 0
u(0,t)=0,u(1,t)=0
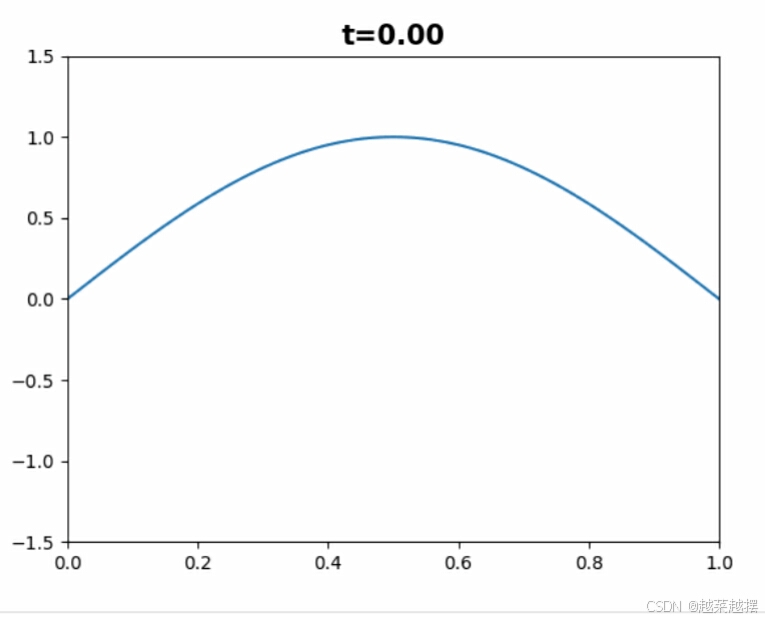
初始状态如图:
这个问题很容易利用分离变量法求出解析解,可以自行尝试,现在直接给出解析解:
u
(
x
,
t
)
=
s
i
n
(
π
x
)
[
c
o
s
(
π
c
t
)
+
1
c
s
i
n
(
π
c
t
)
]
u(x,t)=sin(\pi x)[cos(\pi ct)+ \frac{1}{c}sin(πct)]
u(x,t)=sin(πx)[cos(πct)+c1sin(πct)]
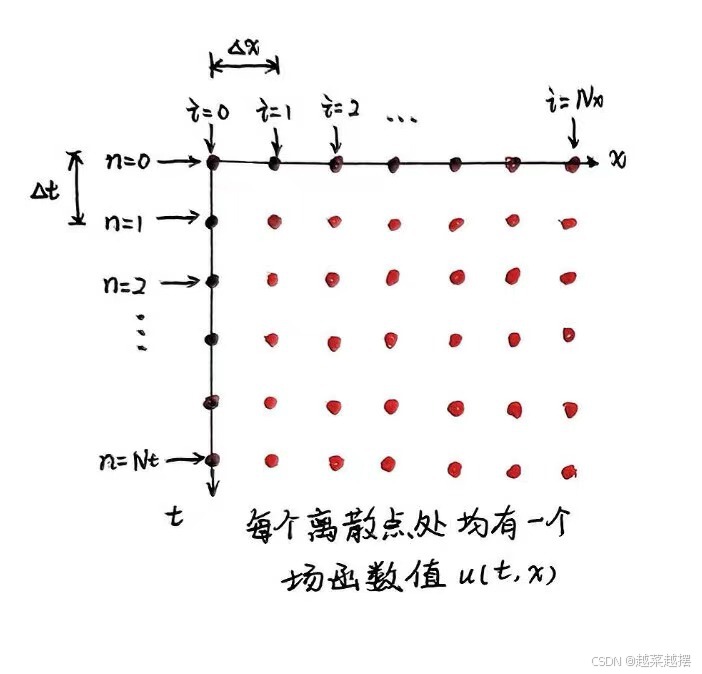
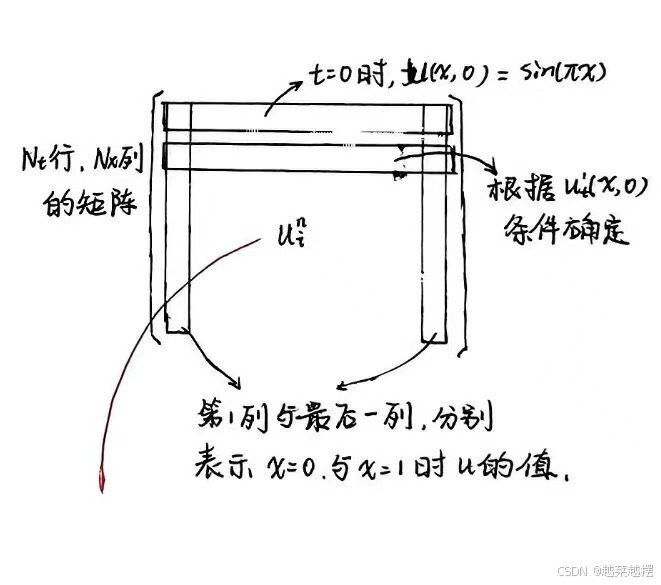
3. 连续方程的有限差分离散
时间、空间离散化,初始边界条件如何处理、方程的离散格式如何给出内部未知场函数,见图:
4. 结果展示
基于上面的离散求解方法,我们得到琴弦振动动态图:
5. Python代码
完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# 定义网格参数
c = 2.
deltax = 0.01
deltat = deltax / 5
r = c**2 * (deltat/deltax)**2
T = 1.5
Nx, Nt = int(1/deltax+1), int(T/deltat+1)
# 初始化数组
U = np.empty((Nt, Nx))
U.fill(1)
x = np.linspace(start=0, stop=1, num=Nx, endpoint=True)
U[0, :] = np.sin(x*np.pi) # np.where(x < 1/3, x*3, 3/2*(1-x))
U[1, :] = U[0, :]
U[:, 0] = 0.
U[:, -1] = 0.
for iteration in range(100):
for n in range(1, Nt-1):
for i in range(1, Nx-1):
U[n+1, i] = -U[n-1, i] + (2-2*r)*U[n, i] + r*U[n, i+1] + r*U[n, i-1]
# 创建一个新的figure对象
fig, ax = plt.subplots()
ax.set_xlim(0, 1)
ax.set_ylim(-1.5, 1.5)
# 初始化数据
line, = ax.plot(x, U[0, :])
def animate(t):
y = U[t, :]
line.set_ydata(y)
ax.set_title(f't={(t-1)*deltat:.2f}', fontsize=15, fontweight='bold')
return line,
# 创建动画
ani = animation.FuncAnimation(fig, animate, frames=range(0, Nt), interval=20, blit=True)
# 显示图形
# plt.show()
ani.save('sin.gif', writer='pillow')
若有不足之处,欢迎批评指正!