函数式自动微分

• 在深度学习中，模型的训练依赖于梯度计算。手动推导梯度公式非常繁琐且容易出错，而自动微分可以自动完成这项工作，大大降低了开发难度。
• MindSpore 采用了函数式自动微分的设计理念，提供了更符合数学直觉的接口 grad 和 value_and_grad。
• grad(func)：计算函数 func 的梯度函数。
• value_and_grad(func)：同时计算函数 func 的值和梯度。

• 函数与计算图

• 
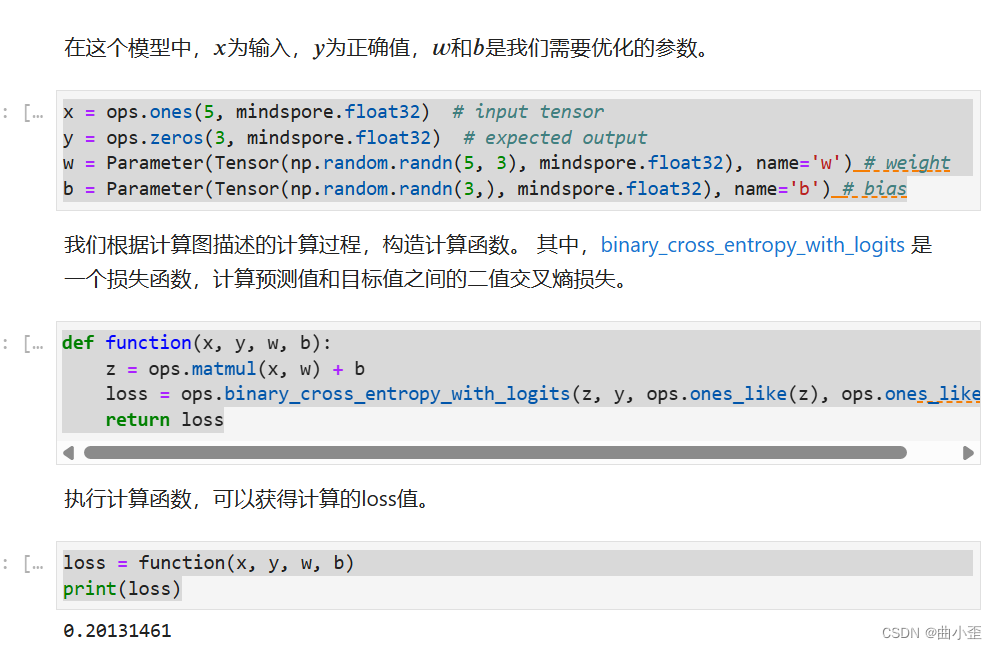
• x：一个形状为 (5,) 的全1浮点数张量，表示输入数据。
• y：一个形状为 (3,) 的全0浮点数张量，表示期望输出（目标值）。
• w：一个形状为 (5, 3) 的可学习参数，表示权重矩阵，初始值为随机的标准正态分布。
• b：一个形状为 (3,) 的可学习参数，表示偏置向量，初始值为随机的标准正态分布。

  
  接着，定义了一个名为 function 的函数，它接受 x、y、w 和 b 作为输入，并执行以下计算：

• 线性变换： z = ops.matmul(x, w) + b
  • 将输入 x 与权重矩阵 w 相乘，然后加上偏置向量 b，得到中间结果 z。
• 损失计算： loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
  • 使用 ops.binary_cross_entropy_with_logits 函数计算二元交叉熵损失。
    • z 是模型的输出logits（未经过sigmoid激活）。
    • y 是期望输出（目标值）。
    • ops.ones_like(z) 和 ops.ones_like(z) 分别表示正类和负类的权重，这里都设为1。

      
      最后，函数返回计算得到的 loss 值。

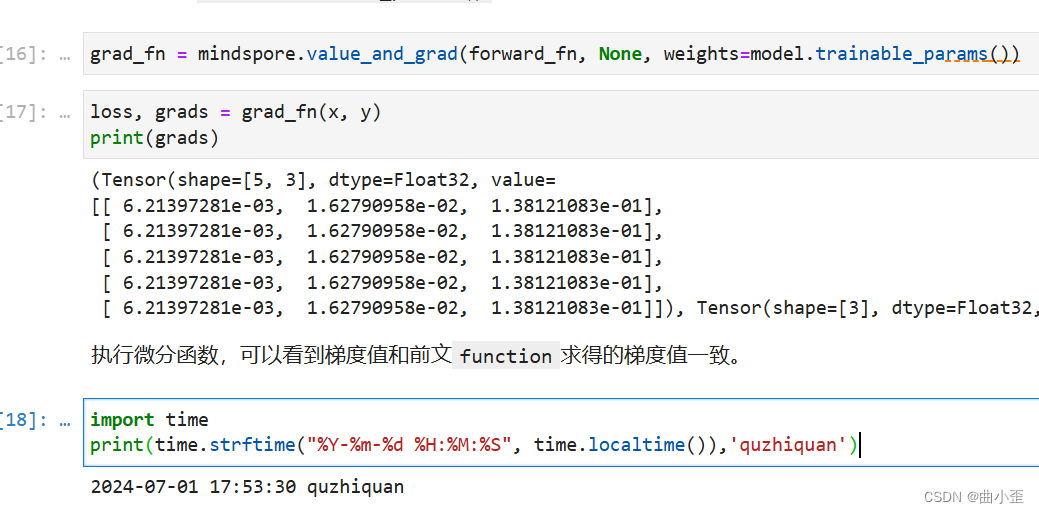
• 微分函数与梯度计算

  • 为了优化模型参数，需要求参数对loss的导数使用自动微分提供的接口mindspore.grad函数，来获得function的微分函数。
    • grad_fn = mindspore.grad(function, (2, 3))

      grads = grad_fn(x, y, w, b)
      print(grads)

    • 
    • 获取梯度函数：
      • grad_fn = mindspore.grad(function, (2, 3))
        • mindspore.grad 函数用于获取 function 对指定参数的梯度函数。
        • (2, 3) 表示我们希望计算 function 对第二个参数 (w) 和第三个参数 (b) 的梯度。
    • 计算梯度：
      • grads = grad_fn(x, y, w, b)
        • 调用 grad_fn，传入输入数据 x、目标值 y、权重 w 和偏置 b，计算 function 对 w 和 b 的梯度。
    • 打印梯度：
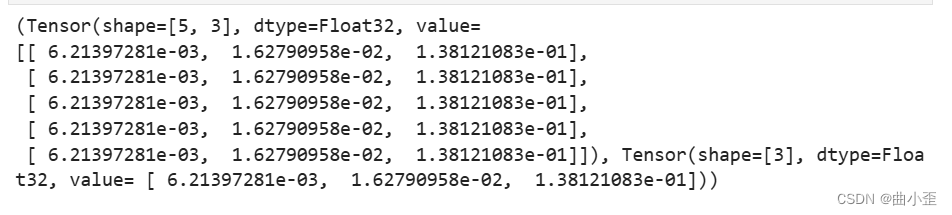
      • print(grads)
      • 输出结果为两个张量，分别对应 w 和 b 的梯度：
      • 第一个张量是 w 的梯度，形状为 (5, 3)。
      • 第二个张量是 b 的梯度，形状为 (3,)。

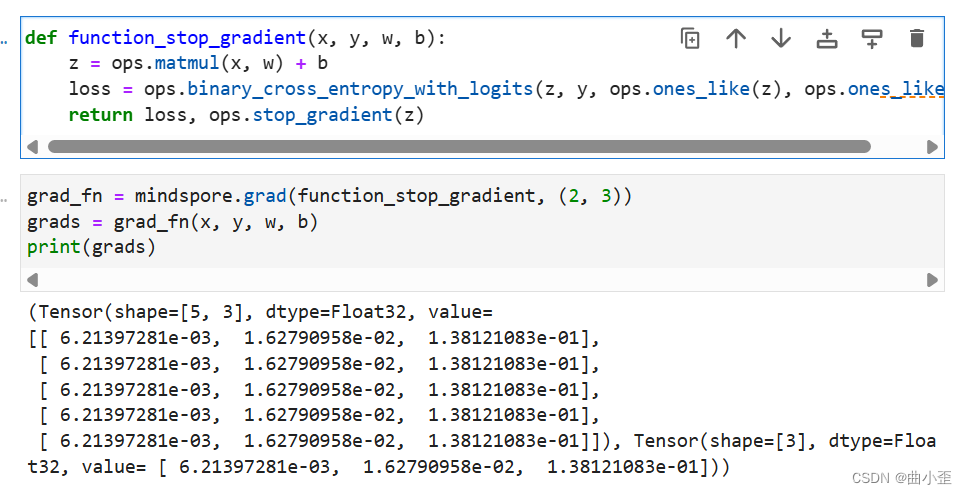
• Stop Gradient

  • Stop Gradient 操作，顾名思义，就是停止梯度的传播。在反向传播过程中，对于被应用 Stop Gradient 的张量，其梯度将被设置为零，并且不会向其依赖的输入张量传播梯度。
  • Stop Gradient 的好处
    • 控制梯度流动： 在某些网络结构中，我们可能希望某些参数不被更新，或者只希望梯度沿着特定路径传播。Stop Gradient 可以精确地控制梯度的流动方向。
    • 训练特定部分： 在迁移学习中，我们通常会冻结预训练模型的部分层，只训练后面的层。Stop Gradient 可以方便地实现这一功能。
    • 实现复杂算法： 许多复杂的深度学习算法，如生成对抗网络（GAN）、强化学习等，都依赖于 Stop Gradient 来实现特定的训练策略。
    • 提高训练稳定性： 在某些情况下，梯度的传播可能会导致梯度爆炸或梯度消失问题，影响模型的训练稳定性。Stop Gradient 可以通过截断梯度传播来缓解这些问题。
    
    • 
       

• Auxiliary data

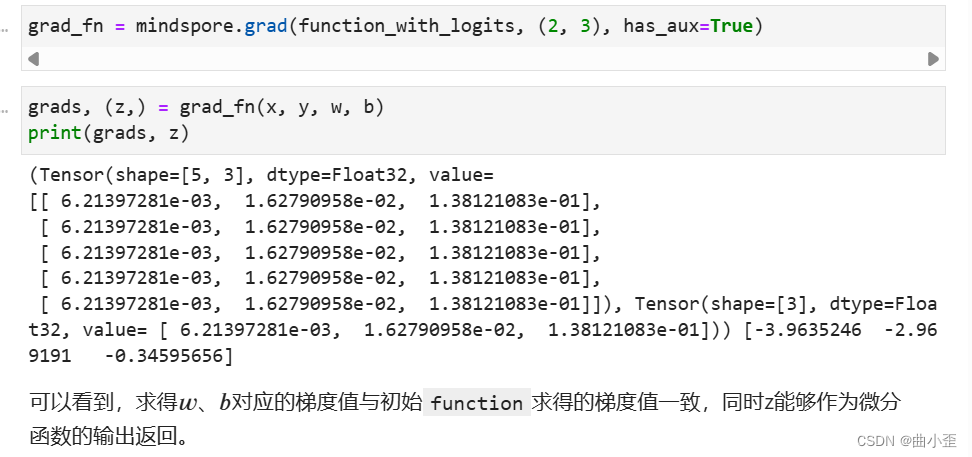
  • Auxiliary data意为辅助数据，是函数除第一个输出项外的其他输出。通常我们会将函数的loss设置为函数的第一个输出，其他的输出即为辅助数据。
  • grad和value_and_grad提供has_aux参数，当其设置为True时，可以自动实现前文手动添加stop_gradient的功能，满足返回辅助数据的同时不影响梯度计算的效果。
  
  • 
     

• 神经网络梯度计算

• 反向传播算法用在哪个环节？

  
  反向传播算法通常用在神经网络的训练环节。具体来说，它在每次迭代中完成以下步骤：

  • 前向传播： 计算当前网络参数下模型的输出。
  • 计算损失： 将模型输出与真实标签比较，得到损失值。
  • 反向传播： 计算损失函数对每个参数的梯度。
  • 参数更新： 根据梯度和优化算法，更新网络参数。
• 反向传播算法的目的是什么？

  
  反向传播算法的目的是通过不断调整神经网络的参数，使得模型在训练数据上的损失最小化。这相当于让模型从错误中学习，逐渐提高其对数据的拟合能力和泛化能力。

• 通俗解释：
  • 可以把神经网络想象成一个学生，训练数据是他的教材，真实标签是标准答案。反向传播算法就是老师批改作业的过程：
  • 学生做题（正向传播）
  • 老师批改，找出错误（计算损失）
  • 老师分析错误原因，告诉学生哪里需要改进（反向传播）
  • 学生根据老师的反馈修改答案（参数更新）
  • 通过不断重复这个过程，学生就能逐渐提高解题能力。
  •