牛顿-拉夫逊优化算法(Newton-Raphson-based optimizer, NBRO)是一种新型的元启发式算法(智能优化算法),该成果由Sowmya等人于2024年2月发表在中科院2区Top SCI期刊《Engineering Applications of Artificial Intelligence》上。
1、算法原理
NRBO受到Newton-Raphson方法的启发,它使用两个规则:Newton-Raphson搜索规则(NRSR)和陷阱避免算子(TAO)以及几组矩阵来探索整个搜索过程,以进一步探索最佳结果。NRSR使用Newton-Raphson方法来提高NRBO的探索能力,并提高收敛速度以达到改进的搜索空间位置。TAO帮助NRBO避免局部最优陷阱,具体算法原理及位置更新可看这篇文章:
2024年新算法-牛顿-拉夫逊优化算法(NRBO)-公式原理详解 Matlab代码免费获取
2、三维路径规划
(1)路径长度代价
本文选择最小化路径长度判断路径是否最优。无人机是通过地面控制站控制的,因此无人机的飞行路径
C
i
C_i
Ci表示由n个航点组成的列表,每一个航点对应路径规划搜索地图中的一个路径节点。假设共有i条飞行路径,
j
j
j个路径节点,每个节点坐标可以表示为
P
i
j
(
x
i
j
,
y
i
j
,
z
i
j
)
P_{ij}( x_{ij}, y_{ij}, z_{ij})
Pij(xij,yij,zij) , 因此路径长度代价
T
1
T_{_1}
T1为
T
1
(
C
i
)
=
∑
j
=
1
n
−
1
P
i
,
j
P
i
,
j
+
1
→
T_1(C_i)=\sum_{j=1}^{n-1}\overrightarrow{P_{i,j}P_{i,j+1}}
T1(Ci)=j=1∑n−1Pi,jPi,j+1
(2)障碍物威胁代价
除了路径长度最优之外,路径规划中的路径还必须要确保无人机的安全运行,因此,引人障碍物威胁代价能够引导无人机躲避实际操作环境中的障碍物。假设飞行过程共有
κ
\kappa
κ个障碍物,用圆柱体来模拟飞行过程中遇到的障碍物,将无人机大小考虑为直径D,每一个障碍物投影的中心坐标点为
O
k
O_k
Ok ,半径为
R
k
R_k
Rk
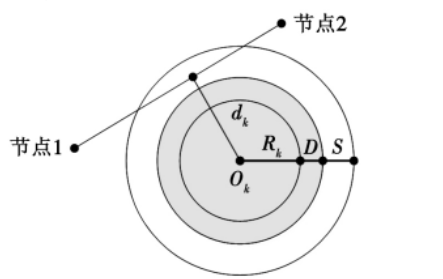
图1 障碍物投影
对于一条给定的从节点1到节点2的路径段,飞行的安全距离为 S,相邻两个路径节点与
O
k
O_k
Ok的垂直距离为
d
k
d_k
dk ,即无人机必须限定在阴影之外的区域飞行,才确保飞行的安全。此时第 i 条路径的障碍物威胁代价
T
2
T_{2}
T2为
T
2
(
C
i
)
=
{
∑
j
=
1
n
−
1
∑
K
=
1
K
max
(
S
+
D
+
R
K
)
−
d
K
D
+
R
K
<
d
K
⩽
S
+
D
+
R
K
0
d
K
>
S
+
D
+
R
K
∞
d
K
⩽
D
+
R
K
T_2(\boldsymbol{C}_i)=\begin{cases}\sum_{j=1}^{n-1}\sum_{K=1}^{K_{\max}}(S+D+R_K)-d_K&D+R_K<d_K\leqslant S+D+R_K\\\\0&d_K>S+D+R_K\\\\\infty&d_K\leqslant D+R_K\end{cases}
T2(Ci)=⎩
⎨
⎧∑j=1n−1∑K=1Kmax(S+D+RK)−dK0∞D+RK<dK⩽S+D+RKdK>S+D+RKdK⩽D+RK
(3)航行高度代价
无人机的平稳飞行决定了路径的平滑程度,稳定的飞行高度不仅能够规划平稳的飞行路径,而且有助于节省燃料,一定程度上减轻了无人机控制系统的负担。另外,在无人机的实际应用中,飞行高度经常被限制在两个给定的极值之间,即必须在适当的高度巡航才能满足测量、航拍及搜索应用等要求。假设最小和最大高度分别为
h
m
i
n
h_{min}
hmin和
h
m
a
x
h_{max}
hmax ,则航行高度代价
T
3
T_3
T3为
T
3
(
C
i
)
=
∑
j
=
1
n
H
i
j
H
i
j
=
{
h
min
−
h
i
j
h
i
j
<
h
min
0
h
min
⩽
h
i
j
⩽
h
max
h
i
j
−
h
max
h
i
j
>
h
max
T_3(\:C_i)\:=\sum_{j=1}^n\:H_{ij}\\H_{ij}=\begin{cases}h_{\min}-h_{ij}&h_{ij}<h_{\min}\\0&h_{\min}\leqslant h_{ij}\leqslant h_{\max}\\h_{ij}-h_{\max}&h_{ij}>h_{\max}\end{cases}
T3(Ci)=j=1∑nHijHij=⎩
⎨
⎧hmin−hij0hij−hmaxhij<hminhmin⩽hij⩽hmaxhij>hmax
式中,
h
i
j
h_{ij}
hij为相对于地面的飞行高度。综合路径最优代价、障碍物威胁代价和航行高度代价 ,得到的路径适应度函数为
T
3
T_{3}
T3为
T
3
(
C
i
)
=
∑
j
=
1
n
H
i
j
H
i
j
=
{
h
min
−
h
i
j
h
i
j
<
h
min
0
h
min
⩽
h
i
j
⩽
h
max
h
i
j
−
h
max
h
i
j
>
h
max
T_3(\:C_i)\:=\:\sum_{j=1}^n\:H_{ij}\\H_{ij}=\begin{cases}h_{\min}-h_{ij}&h_{ij}<h_{\min}\\0&h_{\min}\leqslant h_{ij}\leqslant h_{\max}\\h_{ij}-h_{\max}&h_{ij}>h_{\max}\end{cases}
T3(Ci)=j=1∑nHijHij=⎩
⎨
⎧hmin−hij0hij−hmaxhij<hminhmin⩽hij⩽hmaxhij>hmax
式中,
h
i
j
h_{ij}
hij为相对于地面的飞行高度。综合路径最优代价、障碍物威胁代价和航行高度代价 ,得到的路径适应度函数为
T
(
C
i
)
=
b
1
T
1
(
C
i
)
+
b
2
T
2
(
C
i
)
+
b
3
T
3
(
C
i
)
T(\boldsymbol{C}_i)\:=b_1T_1(\boldsymbol{C}_i)\:+b_2T_2(\boldsymbol{C}_i)\:+b_3T_3(\boldsymbol{C}_i)
T(Ci)=b1T1(Ci)+b2T2(Ci)+b3T3(Ci)
式中
b
1
,
b
2
,
b
3
b_1,b_2,b_3
b1,b2,b3为[0,10]之间的权重系数,通过调整权重系数,满足不同应用的路径要求。如航拍需要无人机稳定飞行在一定的高度上,则可适当增加航行高度代价的权重系数
b
3
b_{3}
b3 ,部分代码如下:
%% 威胁区域绘制
%威胁区域中心坐标
ThreatAreaPostion = [120,120];
%威胁区域半径
ThreatAreaRadius = 30;
%将威胁区域叠加到图上
figure
mesh(Map);
hold on;
for i= 1:size(ThreatAreaRadius)
[X,Y,Z] = cylinder(ThreatAreaRadius(i),50);
X = X + ThreatAreaPostion(i,1);
Y = Y + ThreatAreaPostion(i,2);
Z(2,:) = Z(2,:) + 50;%威胁区域高度
mesh(X,Y,Z)
end
%% 设置起始点和终止
startPoint = [50,0,10];
endPoint = [200,200,20];
plot3(startPoint(1),startPoint(2),startPoint(3),'ro');
text(startPoint(1),startPoint(2),startPoint(3),'起点','Color','k','FontSize',15)
plot3(endPoint(1),endPoint(2),endPoint(3),'r*');
text(endPoint(1),endPoint(2),endPoint(3),'终点','Color','k','FontSize',15)
title('地图信息')
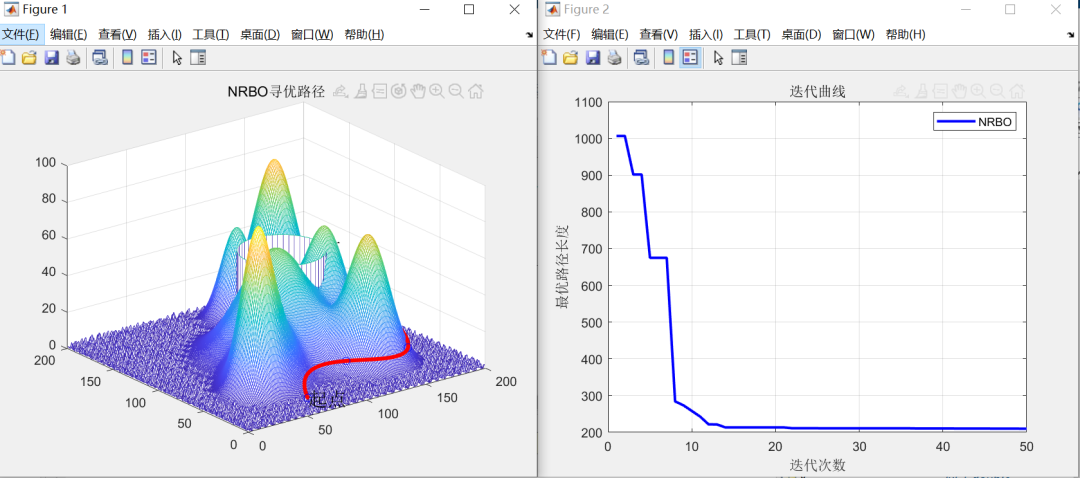
3、运行结果
朱润泽,赵静,蒋国平,等.基于改进粒子群算法的无人机三维路径规划[J].南京邮电大学学报(自然科学版),1-10[2024-07-17].
完整代码下载:
基于牛顿-拉夫逊优化算法(Newton-Raphson-based optimizer, NBRO)的无人机三维路径规划