数据结构与算法：顺序查找、折半查找、二叉排序树

一、顺序查找

顺序查找又称线性查找，对于顺序表和链表都适用。对于顺序表，可通过数组下标递增来顺序扫描每个元素；对于链表，则通过指针next来依次扫描每个元素。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
typedef int ElemType;
typedef struct{
	ElemType *elem; //整形指针,申请的堆空间的起始地址存入elem 
	int TableLen; //存储动态数组里边元素的个数 
}SSTable;

void ST_Init(SSTable &ST,int len){
	//多申请一个位置，存哨兵
	ST.TableLen=len+1;
	ST.elem=(ElemType *)malloc(sizeof(ElemType)*ST.TableLen);
	int i;
	srand(time(NULL)); //随机数生成
	for(i=1;i<ST.TableLen;i++){
		ST.elem[i]=rand()%100;
	} 
}

void ST_print(SSTable ST){
	int i;
	for(i=1;i<ST.TableLen;i++){
		printf("%3d",ST.elem[i]);
	}
	printf("\n");
}

int Search_Seq(SSTable ST,ElemType key){
	ST.elem[0]=key; //key存在零号位置，作为哨兵，在循环时，可以少些i>=0 
	int i;
	for(i=ST.TableLen-1;ST.elem[i]!=key;i--);
	return i;	
}

//顺序查找
int main(){
	SSTable ST;
	ST_Init(ST,10); 
	ST_print(ST);
	ElemType key;
	printf("please input search key:\n");
	scanf("%d",&key);
	int pos;
	pos=Search_Seq(ST,key);
	if(pos){
		printf("find pos,pos=%d\n",pos);
	}
	else{
		printf("not find\n");
	}
	return 0;
}

二、折半查找

折半查找又称二分查找，仅适用于有序的顺序表。

基本思想：首先将给定值key与表中中间位置的元素比较，若相等则查找成功，返回该元素的存储位置，若不等，则所需查找的元素只能中间元素以外的前半部分或后半部分。然后缩小范围继续进行同样的查找。

1、初始化顺序表，随机10个元素

2、使用qsort进行排序，排序完毕后，打印

3、输入要查找的元素值，存入变量key中

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef int ElemType;
typedef struct{
	ElemType *elem; //整形指针,申请的堆空间的起始地址存入elem 
	int TableLen; //存储动态数组里边元素的个数 
}SSTable;

void ST_Init(SSTable &ST,int len){
	ST.TableLen=len;
	ST.elem=(ElemType *)malloc(sizeof(ElemType)*ST.TableLen);
	int i;
	srand(time(NULL)); //随机数生成
	for(i=0;i<ST.TableLen;i++){
		ST.elem[i]=rand()%100;
	} 
}

void ST_print(SSTable ST){
	int i;
	for(i=1;i<ST.TableLen;i++){
		printf("%3d",ST.elem[i]);
	}
	printf("\n");
}

int BinarySearch(SSTable L,ElemType key){
	int low=0;
	int high=L.TableLen-1;
	int mid;
	while(low<=high){
		mid=(low+high)/2;
		if(key>L.elem[mid]){
			low=mid+1;
		}
		else if(key<L.elem[mid]){
			high=mid-1;
		}
		else{
			return mid;
		}
	}
	return -1;
} 

//函数名中存储的是函数的入口地址，也是一个指针，是函数指针类型 
//qsort规定，如果left指针指向的值大于right指针指向的值，返回正值；小于，返回负值 
int compare(const void *left,const void *right){
	return *(int*)left-*(int*)right; //从小到大 
}

//二分查找
int main(){
	SSTable ST;
	ST_Init(ST,10); 
	ST_print(ST);
	qsort(ST.elem,ST.TableLen,sizeof(ElemType),compare);
	ST_print(ST);
	ElemType key;
	printf("please input search key:\n");
	scanf("%d",&key);
	int pos;
	pos=BinarySearch(ST,key);
	if(pos!=-1){
		printf("find pos,pos=%d\n",pos);
	}
	else{
		printf("not find\n");
	}
	return 0;
}

三、二叉排序树

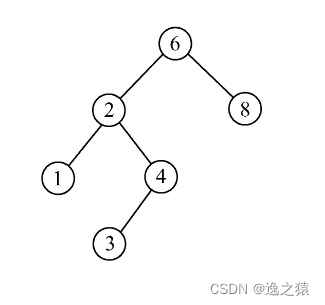
二叉排序树（二叉查找树）或是一颗空树，或是具有下列特性的二叉树：

1、若左子树非空，则左子树上所有结点的值均小于根结点的值

2、若右子树非空，则右子树上所有结点的值均大于根结点的值

3、左、右子树也分别是一颗二叉排序树

二叉排序树的最大查找次数是树的高度

二叉排序树新建，中序遍历，查找，删除

#include <stdio.h>
#include <stdlib.h>
 
typedef int KeyType;
typedef struct BSTNode{
	KeyType key;
	struct BSTNode *lchild,*rchild;
}BSTNode,*BiTree;

//递归 
int BST_Insert(BiTree &T,KeyType k){
	if(T==NULL){
		//为新结点申请空间，第一个结点作为树根，后面递归再进入的不是树根，是叶子结点
		T=(BiTree)malloc(sizeof(BSTNode));
		T->key=k;
		T->lchild=T->rchild=NULL;
		return 1; //代表插入成功 
	} 
	else if(k==T->key){
		return 0; // 发现相同元素，就不插入 
	} 
	else if(k<T->key){
		return BST_Insert(T->lchild,k);
	}
	else{
		return BST_Insert(T->rchild,k);
	}
	
}

void Create_BST(BiTree &T,KeyType str[],int len){
	int i;
	for(i=0;i<len;i++){
		BST_Insert(T,str[i]); //把某一个结点放入二叉查找树 
	}	
}

//中序遍历 
void InOrder(BiTree T){
	if(T!=NULL){
		InOrder(T->lchild); //打印左子树 
		//putchar(p->c);
		printf("%3d",T->key);
		InOrder(T->rchild); //打印右子树 
	}
} 

BiTree BST_Search(BiTree T,KeyType k,BiTree &parent){
	parent=NULL;
	while(T!=NULL&&k!=T->key){
		parent=T;
		if(k>T->key){
			T=T->rchild;
		}
		else{
			T=T->lchild;
		}
	}
	return T;
}

void DeleteNode(BiTree &root,KeyType x){
	if(root==NULL){
		return;
	}
	if(root->key>x){
		DeleteNode(root->lchild,x);
	}
	else if(root->key<x){
		DeleteNode(root->rchild,x);
	}
	else{ // 查找到了删除结点 
		if(root->lchild==NULL){ // 左子树为空，右子树直接顶上去 
			BiTree tempNode=root; // 临时存着，一会儿free 
			root=root->rchild;
			free(tempNode); 
		}
		else if(root->rchild==NULL){ // 右子树为空，左子树直接顶上去 
			BiTree tempNode=root;
			root=root->lchild;
			free(tempNode); 
		}
		else{ // 左右子树都不为空
		    //左子树的最大数据（右子树的最小数据）代替要删除的结点
			BiTree tempNode=root->lchild;
			while(tempNode->rchild!=NULL){ // 向右找到最大的
			    tempNode=tempNode->rchild; 
			}
			root->key=tempNode->key; // 把tempNode对应的值替换到要删除的值的位置上
			DeleteNode(root->lchild,tempNode->key); //在左子树上找到tempNode值，把其删除 
		}
	}
}

//二叉排序树新建，中序遍历，查找 ，删除 
int main(){
	BiTree T=NULL; // 树根
	BiTree parent; // 存储父亲结点的地址值
	KeyType str[7]={54,20,66,40,28,79,58}; // 将要进入二叉排序树的元素值
	Create_BST(T,str,7);
	InOrder(T);
	printf("\n");
	BiTree search;
	search=BST_Search(T,40,parent);
	if(search){
		printf("find key %d\n",search->key); 
	}
	else{
		printf("not find\n");
	}
	DeleteNode(T,40);
	InOrder(T); 
	return 0; 
}

数据结构与算法：顺序查找、折半查找、二叉排序树

悦读