做了那么多年开发,自学了很多门编程语言,我很明白学习资源对于学一门新语言的重要性,这些年也收藏了不少的Python干货,对我来说这些东西确实已经用不到了,但对于准备自学Python的人来说,或许它就是一个宝藏,可以给你省去很多的时间和精力。
别在网上瞎学了,我最近也做了一些资源的更新,只要你是我的粉丝,这期福利你都可拿走。
我先来介绍一下这些东西怎么用,文末抱走。
(1)Python所有方向的学习路线(新版)
这是我花了几天的时间去把Python所有方向的技术点做的整理,形成各个领域的知识点汇总,它的用处就在于,你可以按照上面的知识点去找对应的学习资源,保证自己学得较为全面。
最近我才对这些路线做了一下新的更新,知识体系更全面了。
(2)Python学习视频
包含了Python入门、爬虫、数据分析和web开发的学习视频,总共100多个,虽然没有那么全面,但是对于入门来说是没问题的,学完这些之后,你可以按照我上面的学习路线去网上找其他的知识资源进行进阶。
(3)100多个练手项目
我们在看视频学习的时候,不能光动眼动脑不动手,比较科学的学习方法是在理解之后运用它们,这时候练手项目就很适合了,只是里面的项目比较多,水平也是参差不齐,大家可以挑自己能做的项目去练练。
(4)200多本电子书
这些年我也收藏了很多电子书,大概200多本,有时候带实体书不方便的话,我就会去打开电子书看看,书籍可不一定比视频教程差,尤其是权威的技术书籍。
基本上主流的和经典的都有,这里我就不放图了,版权问题,个人看看是没有问题的。
(5)Python知识点汇总
知识点汇总有点像学习路线,但与学习路线不同的点就在于,知识点汇总更为细致,里面包含了对具体知识点的简单说明,而我们的学习路线则更为抽象和简单,只是为了方便大家只是某个领域你应该学习哪些技术栈。
(6)其他资料
还有其他的一些东西,比如说我自己出的Python入门图文类教程,没有电脑的时候用手机也可以学习知识,学会了理论之后再去敲代码实践验证,还有Python中文版的库资料、MySQL和HTML标签大全等等,这些都是可以送给粉丝们的东西。
这些都不是什么非常值钱的东西,但对于没有资源或者资源不是很好的学习者来说确实很不错,你要是用得到的话都可以直接抱走,关注过我的人都知道,这些都是可以拿到的。
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
这个方程可以转化为:
磷(秒|G秒)=磷(G秒|秒)磷(秒)磷(G秒)
结果符合贝叶斯定理
为了解决我们的问题,即一个人是瑞士人的概率,如果我们知道他或她说德语——我们所要做的就是计算右边。我们从之前的练习中已经知道
磷(G秒|秒)=0.64
和
磷(秒)=0.00112
世界上以德语为母语的人数相当于 1.01 亿,所以我们知道
磷(G秒)=1017500=0.0134667
最后,我们可以计算 磷(秒|G秒) 通过替换我们方程中的值:
磷(秒|G秒)=磷(G秒|秒)磷(秒)磷(G秒)=0.64*0.001120.0134667=0.0532276
大约有 840 万人居住在瑞士。大约 64% 的人会说德语。地球上大约有75亿人。
如果一些外星人随机地向地球人发出光芒,那么他是说德语的瑞士人的可能性有多大?
我们有活动
秒: 瑞士人 G秒: 德语
磷(秒)=8.47500=0.00112磷(一个|乙)=磷(乙|一个)磷(一个)磷(乙)
磷(一个|乙) 是条件概率 一个,给定 乙 (后验概率), 磷(乙) 是先验概率 乙 和 磷(一个) 的先验概率 一个. 磷(乙|一个) 是条件概率 乙 给予 一个,称为可能性。
朴素贝叶斯分类器的一个优点是它只需要少量的训练数据来估计分类所需的参数。因为假设了自变量,所以只需要确定每个类的变量的方差,而不是整个协方差矩阵。
入门练习
让我们踏上火车之旅,创建我们的第一个非常简单的朴素贝叶斯分类器。假设我们在汉堡市,我们想前往慕尼黑。我们将不得不在美因河畔法兰克福换乘火车。我们从以前的火车旅行中知道,我们从汉堡出发的火车可能会晚点,我们将赶不上法兰克福的转机火车。我们无法赶上接驳列车的可能性取决于我们可能的延误有多高。接驳列车的等待时间不会超过五分钟。有时另一列火车也会晚点。
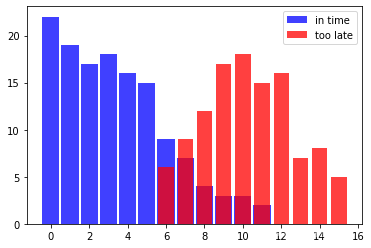
以下列表“in_time”(从汉堡出发的火车及时到达以赶上前往慕尼黑的连接火车)和“too_late”(错过连接火车)是显示几周内情况的数据。每个元组的第一个组件显示火车晚点的分钟数,第二个组件显示发生这种情况的时间。
# 元组包括(train1 的延迟时间,次数)
# 元组是 (分钟, 次数)
in_time = [( 0 , 22 ), ( 1 , 19 ), ( 2 , 17 ), ( 3 , 18 ),
( 4 , 16 ), ( 5 , 15 ), ( 6 , 9 ), ( 7 , 7 ),
( 8 , 4 ), ( 9 , 3 ), ( 10 , 3), ( 11 , 2 )]
too_late = [( 6 , 6 ), ( 7 , 9 ), ( 8 , 12 ), ( 9 , 17 ),
( 10 , 18 ), ( 11 , 15 ), ( 12 , 16 ), ( 13 , 7 ),
( 14 , 8 ), ( 15 , 5 )]
% matplotlib内联
导入 matplotlib.pyplot 作为 plt
X , Y = zip ( * in_time )
X2 , Y2 = zip ( * too_late )
bar_width = 0.9
plt 。bar ( X , Y , bar_width , color = “blue” , alpha = 0.75 , label = “in time” )
bar_width = 0.8
plt . bar ( X2 , Y2 , bar_width , color = “red” , alpha = 0.75 , label = “too late” )
plt . 传奇( loc = ‘右上角’ )
plt 。显示()
从这个数据我们可以推断出,如果我们迟到一分钟,赶上接驳列车的概率是 1,因为我们有 19 个成功案例并且没有错过,即在 ‘too_late’ 中没有以 1 作为第一个组件的元组。
我们将表示事件“火车及时到达以赶上连接的火车” 秒 (成功)和“不幸”事件“火车来得太晚,无法赶上连接的火车” 米 (错过)
我们现在可以正式定义“因为我们迟到 1 分钟而赶上火车”的概率:
磷(秒|1)=19/19=1
我们使用了元组的事实 (1,19) 在 ‘in_time’ 中,并且在 ‘too_late’ 中没有第一个组件 1 的元组
如果我们迟到 6 分钟,那么赶上前往慕尼黑的联运火车就变得至关重要了。然而,机会仍然是 60%:
磷(秒|6)=9/9+6=0.6
因此,知道我们迟到 6 分钟而错过火车的概率是:
磷(米|6)=6/9+6=0.4
我们可以编写一个“分类器”函数,它会给出赶上连接列车的概率:
in_time_dict = dict ( in_time )
too_late_dict = dict ( too_late )
def catch_the_train ( min ):
s = in_time_dict 。get ( min , 0 )
如果 s == 0 :
返回 0
否则:
m = too_late_dict 。get ( min , 0 )
返回 s / ( s + m )
对于 分钟 在 范围(- 1 , 13 ):
打印(分钟, catch_the_train (分钟))
输出:
-1 0
0 1.0
1 1.0
2 1.0
3 1.0
4 1.0
5 1.0
6 0.6
7 0.4375
8 0.25
9 0.15
10 0.14285714285714285
11 0.11764705882352941
12 0
朴素贝叶斯分类器示例
准备好数据
我们将使用一个名为’person_data.txt’的文件。它包含 100 个随机人物数据,男性和女性,带有体型、体重和性别标签。
将 numpy 导入****为 np
性别 = [ “男” , “女” ]
人 = []
与 打开(“数据/ person_data.txt” ) 作为 FH :
用于 线 在 FH :
人。追加(行。带()。分裂())
firstnames = {}
高度 = {}
为 性别 在 性别:
firstnames [性别] = [ X [ 0 ] 为 X 中 的人 如果 X [ 4 ] ==性别]
高度[性别] = [ X [ 2 ] 对于 X 在 人 如果 x [ 4 ] ==性别]
高度[性别] = np . 数组(高度[性别], np . int )
用于 性别 的 (“女性” , “男” ):
打印(性别 + “:” )
打印(firstnames [性别] [:10 ])
打印(高度[性别] [:10 ])
输出:
女性:
[“斯蒂芬妮”、“辛西娅”、“凯瑟琳”、“伊丽莎白”、“卡罗尔”、“克里斯蒂娜”、“贝弗利”、“莎伦”、“丹尼斯”、“丽贝卡”]
[149 174 183 138 145 161 179 162 148 196]
男性:
[“兰迪”、“杰西”、“大卫”、“斯蒂芬”、“杰瑞”、“比利”、“厄尔”、“托德”、“马丁”、“肯尼思”]
[184 175 187 192 204 180 184 174 177 200]
警告:Python 类和朴素贝叶斯类之间可能存在一些混淆。我们尽可能通过明确说明其含义来避免它!
设计要素类
我们现在将为特征定义一个 Python 类“Feature”,稍后我们将使用它进行分类。
Feature 类需要一个标签,例如“heights”或“firstnames”。如果特征值是数字的,我们可能希望将它们“装箱”以减少可能的特征值的数量。我们的人的身高范围很大,我们的朴素贝叶斯类“男性”和“女性”只有 50 个测量值。我们将通过将 bin_width 设置为 5 将它们分为“130 到 134”、“135 到 139”、“140 到 144”等范围。没有办法对名字进行分箱,因此 bin_width 将设置为 None。
方法频率返回特定特征值或分箱范围的出现次数。
from collections import Counter
import numpy as np
课程 特点:
def __init__ ( self , data , name = None , bin_width = None ):
self 。姓名 = 姓名
自我。bin_width = bin_width
如果 bin_width :
self 。分钟, 自我。max = min ( data ), max ( data )
bins = np 。范围((自我。分钟 // bin_width ) * bin_width ,
(自我。最大 // bin_width ) * bin_width ,
bin_width )
频率, 仓 = NP 。直方图(数据, 箱)
自我。freq_dict = dict ( zip ( bins , freq ))
self 。freq_sum = sum ( freq )
else :
self. freq_dict = dict ( Counter ( data ))
self 。freq_sum = 总和(自我。freq_dict 。值())
def 频率(self , value ):
如果 self 。bin_width :
value = ( value // self . bin_width ) * self . bin_width
如果 值 在 self 中。freq_dict :
返回 self 。freq_dict [值]
否则:
返回 0
我们现在将为人物数据集的高度值创建两个要素类 Feature。一个要素类包含朴素贝叶斯类“男性”的高度和一类“女性”的高度:
FTS = {}
为 性别 在 性别:
FTS [性别] = 特性(高度[性别], 名称=性别, bin_width = 5 )
打印(性别, FTS [性别] 。freq_dict )
输出:
男 {160: 5, 195: 2, 180: 5, 165: 4, 200: 3, 185: 8, 170: 6, 155: 1, 190: 8, 175: 7}
女性 {160: 8, 130: 1, 165: 11, 135: 1, 170: 7, 140: 0, 175: 2, 145: 3, 180: 4, 150: 5, 185: 0, } 155: 7
频率分布条形图
我们打印了我们的 bin 的频率,但在条形图中看到这些值要好得多。我们将使用以下代码执行此操作:
对于 性别 中的 性别:
频率 = 列表(fts [性别] . freq_dict . items ())
频率。排序(键=拉姆达 X : X [ 1 ])
X , ÿ = 拉链(*频率)
颜色 = “蓝色” 如果 性别== “男性” 其他 “红色”
bar_width = 4 ,如果 性别== “男性” 否则 3
plt 。bar ( X , Y , bar_width , 颜色=颜色, alpha = 0.75 , 标签=性别)
PLT 。图例(loc = ‘右上角’ )
plt 。显示()
我们现在必须用 Python 设计一个朴素贝叶斯类。我们将其称为 NBclass。一个 NBclass 包含一个或多个要素类。NBclass 的名称将存储在 self.name 中。
类 NBclass :
def __init__ ( self , name , * features ):
self 。特征 = 特征
自我。姓名 = 姓名
DEF probability_value_given_feature (自,
FEATURE_VALUE ,
特征):
“”“
p_value_given_feature返回概率P
为特征的FEATURE_VALUE‘值’到occurr
对应于P(d_i | p_j)
其中d_i是特征的特征变量i
‘’”
如果 功能。freq_sum == 0 :
返回 0
else :
返回 特征。频率(FEATURE_VALUE ) / 特征。频率总和
在下面的代码中,我们将创建具有一个特征的 NBclasses,即高度特征。我们将使用我们之前创建的 fts 的要素类:
cls = {}
用于 性别 中的 性别:
cls [性别] = NBclass (性别, fts [性别])
创建简单朴素贝叶斯分类器的最后一步是编写一个类“Classifier”,它将使用我们的类“NBclass”和“Feature”。
类 分类器:
def __init__ ( self , * nbclasses ):
self 。nbclasses = nbclasses
def prob ( self , * d , best_only = True ):
nbclasses = self 。nbclasses
probability_list = []
为 nbclass 在 nbclasses :
FTRS = nbclass 。特征
prob = 1
for i in range ( len ( ftrs )):
prob *= nbclass 。probability_value_given_feature ( d [ i ], ftrs [ i ])
概率列表。追加( (概率, nbclass 。名称) )
prob_values = [ ˚F [ 0 ] 为 ˚F 在 probability_list ]
prob_sum = 总和(prob_values )
如果 prob_sum == 0 :
number_classes = LEN (自我。nbclasses )
PL = []
为 prob_element 在 probability_list :
PL 。追加( (( 1 / number_classes ), prob_element [ 1]))
probability_list = PL
否则:
probability_list = [ (p [ 0 ] / prob_sum , p [ 1 ]) 为 p 在 probability_list ]
如果 best_only :
返回 最大值(probability_list )
否则:
返回 probability_list
我们将创建一个具有一个要素类“高度”的分类器。我们使用 130 到 220 厘米之间的值对其进行检查。
c = 分类器( cls [ “male” ], cls [ “female” ])
对于 我 在 范围(130 , 220 , 5 ):
打印(我, Ç 。概率(我, best_only =假))
输出:
130 [(0.0, ‘男’), (1.0, ‘女’)]
135 [(0.0, ‘男’), (1.0, ‘女’)]
140 [(0.5, ‘男’), (0.5, ‘女’)]
145 [(0.0,‘男性’),(1.0,‘女性’)]
150 [(0.0, ‘男’), (1.0, ‘女’)]
155 [(0.125,‘男性’),(0.875,‘女性’)]
160 [(0.38461538461538469, ‘男’), (0.61538461538461542, ‘女’)]
165 [(0.26666666666666666, ‘男’), (0.733333333333333328, ‘女’)]
170 [(0.46153846153846162, ‘男’), (0.53846153846153855, ‘女’)]
175 [(0.77777777777777779, ‘男’), (0.222222222222222224, ‘女’)]
180 [(0.55555555555555558, ‘男’), (0.444444444444444448, ‘女’)]
185 [(1.0, ‘男’), (0.0, ‘女’)]
190 [(1.0, ‘男’), (0.0, ‘女’)]
195 [(1.0, ‘男’), (0.0, ‘女’)]
200 [(1.0, ‘男’), (0.0, ‘女’)]
205 [(0.5, ‘男’), (0.5, ‘女’)]
210 [(0.5, ‘男’), (0.5, ‘女’)]
现在能在网上找到很多很多的学习资源,有免费的也有收费的,当我拿到1套比较全的学习资源之前,我并没着急去看第1节,我而是去审视这套资源是否值得学习,有时候也会去问一些学长的意见,如果可以之后,我会对这套学习资源做1个学习计划,我的学习计划主要包括规划图和学习进度表。
分享给大家这份我薅到的免费视频资料,质量还不错,大家可以跟着学习
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!