简介
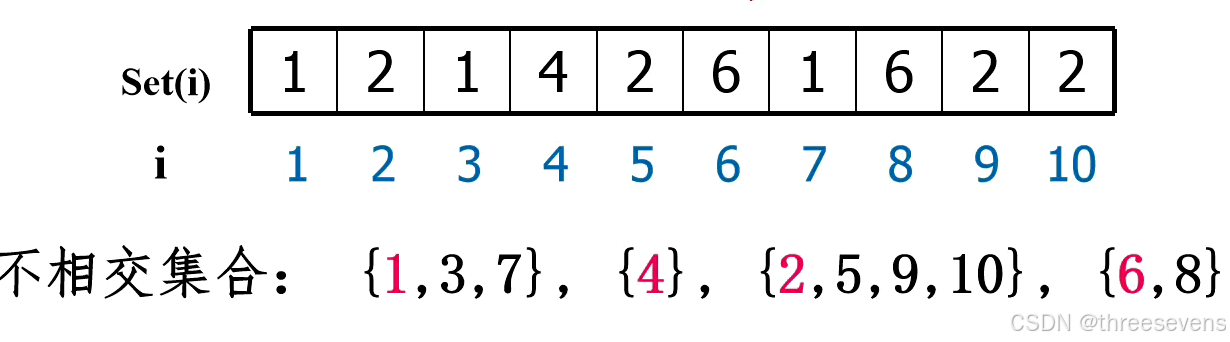
问题描述:将编号为1-N的N个对象划分为不相交集合,在每个集合中,选择其中的某个元素代表所在集合。
常见两种操作:
1.合并两个集合
2.查找某元素属于哪个集合
实现方法1
用编号最小的元素标记所在集合;
定义一个数组Set[1...n],其中Set[i]表示元素i所在的集合
效率分析1
查找:O(1)
find(x)
{
return Set[x];
}合并:O(N)
Merge(a, b)
{
i = min(a, b);
j = max(a, b);
for(k = 1; k <= N; k++)
{
if(Set[k] == j)
{
Set[k] = i;
}
}
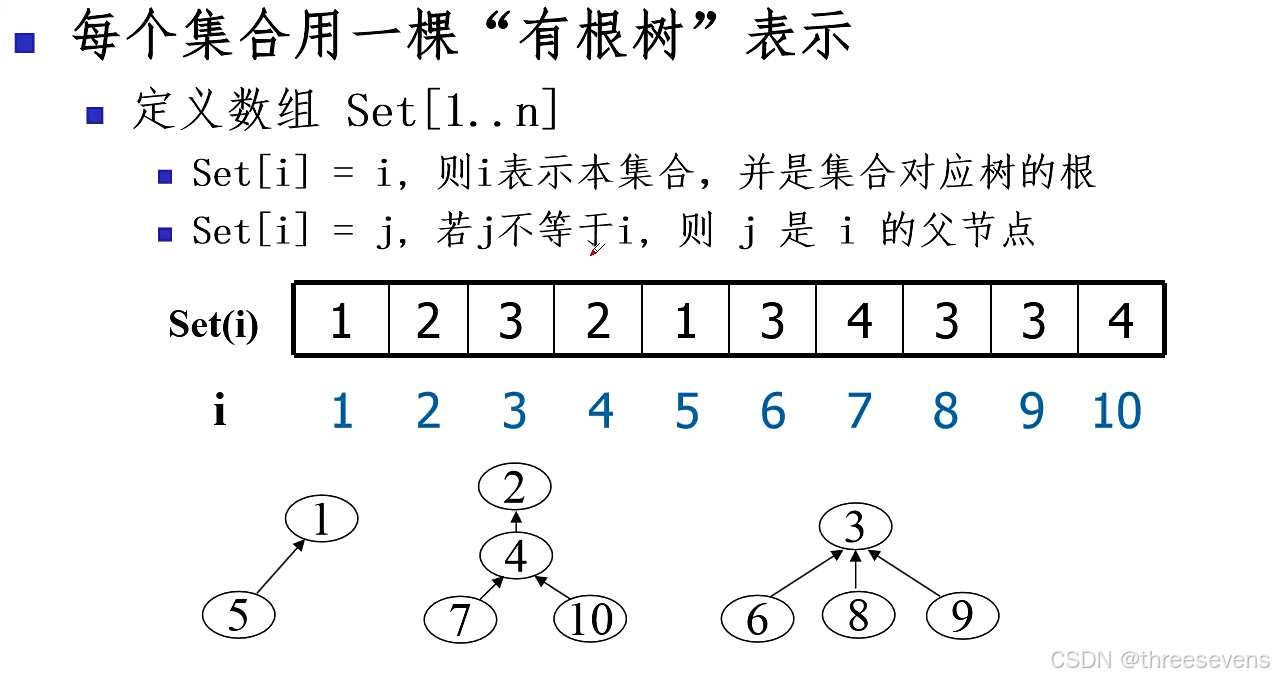
}实现方法2
效率分析2
查找:最坏为O(N),一般为O(log N)
find(x)
{
r = x;
while(Set[t] != r)
r = Set[r];
return r;
}合并:O(1)
merge(a, b)
{
Set[a] = b;
}最坏情况避免
例1
思路:并查集模板,计算集合数量即可
#include<iostream>
using namespace std;
int bin[1002];
int findx(int x)
{
int r = x;
while(bin[r] != r)
r = bin[r];
return r;
}
void merge(int x, int y)
{
int fx, fy;
fx = findx(x);
fy = findx(y);
if(fx != fy)
bin[fx] = fy;
}
int main()
{
int n, m, x, y, count = -1;
while(scanf("%d", &n), n)
{
for(int i = 1; i <= n; i++)
{
bin[i] = i;
}
for(scanf("%d", &m); m > 0; m--)
{
scanf("%d %d", &x, &y);
merge(x, y);
}
for(int i = 1; i <= n; i++)
{
if(bin[i] == i)
{
count ++;
}
}
printf("%d\n", count);
}
return 0;
}例2
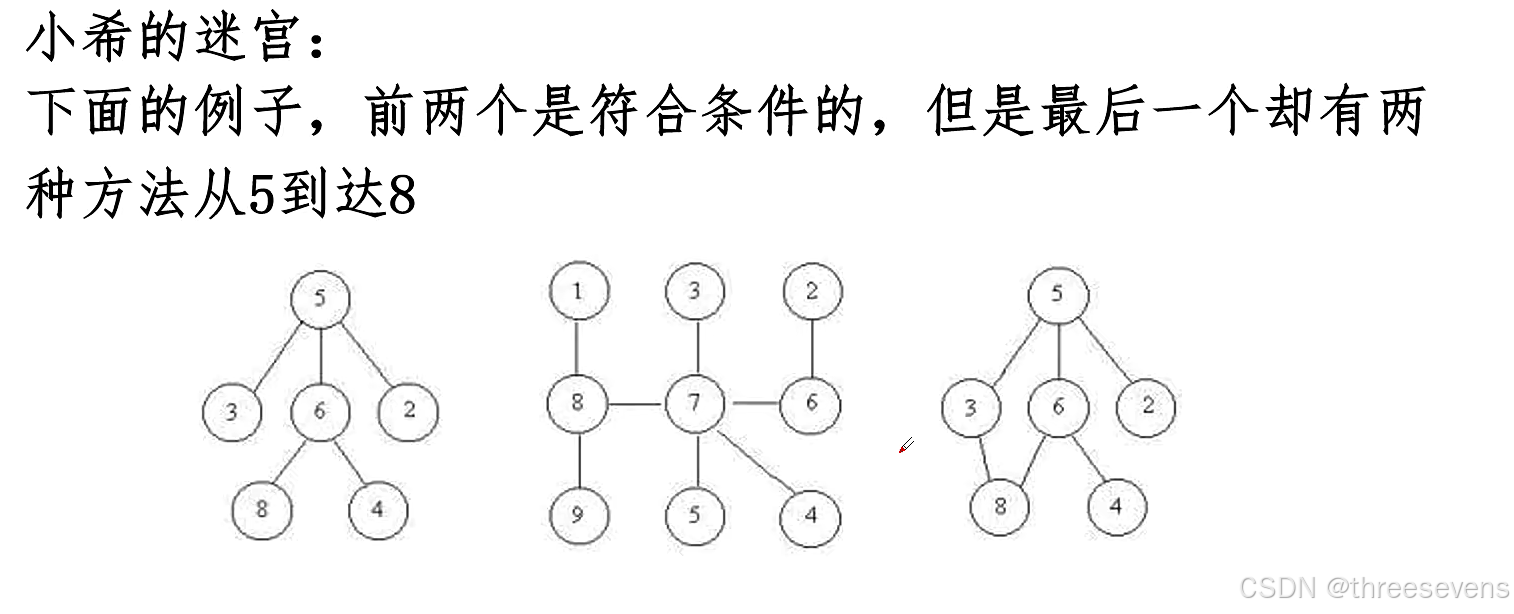
小希希望任意两个房间有且仅有一条路径可以相通(除非走了回头路)。小希现在把她的设计图给你,让你帮忙判断她的设计图是否符合她的设计思路。
思路:判断迷宫是否有环
最小生成树
Kruskal算法
用于求最小生成树
理论基础:MST性质:对于一个连通图,至少存在一棵最小生成树,包含最短的这条边。
可以采用反证法进行证明
算法步骤:
一、把原始图的N个节点看成N个独立子图;
二、每次选取当前最短的边,若边的两端点属于不同的子图,则加入该边;否则放弃
三、循环操作步骤二,直到有N-1条边;
例3
分析:计算最小生成树