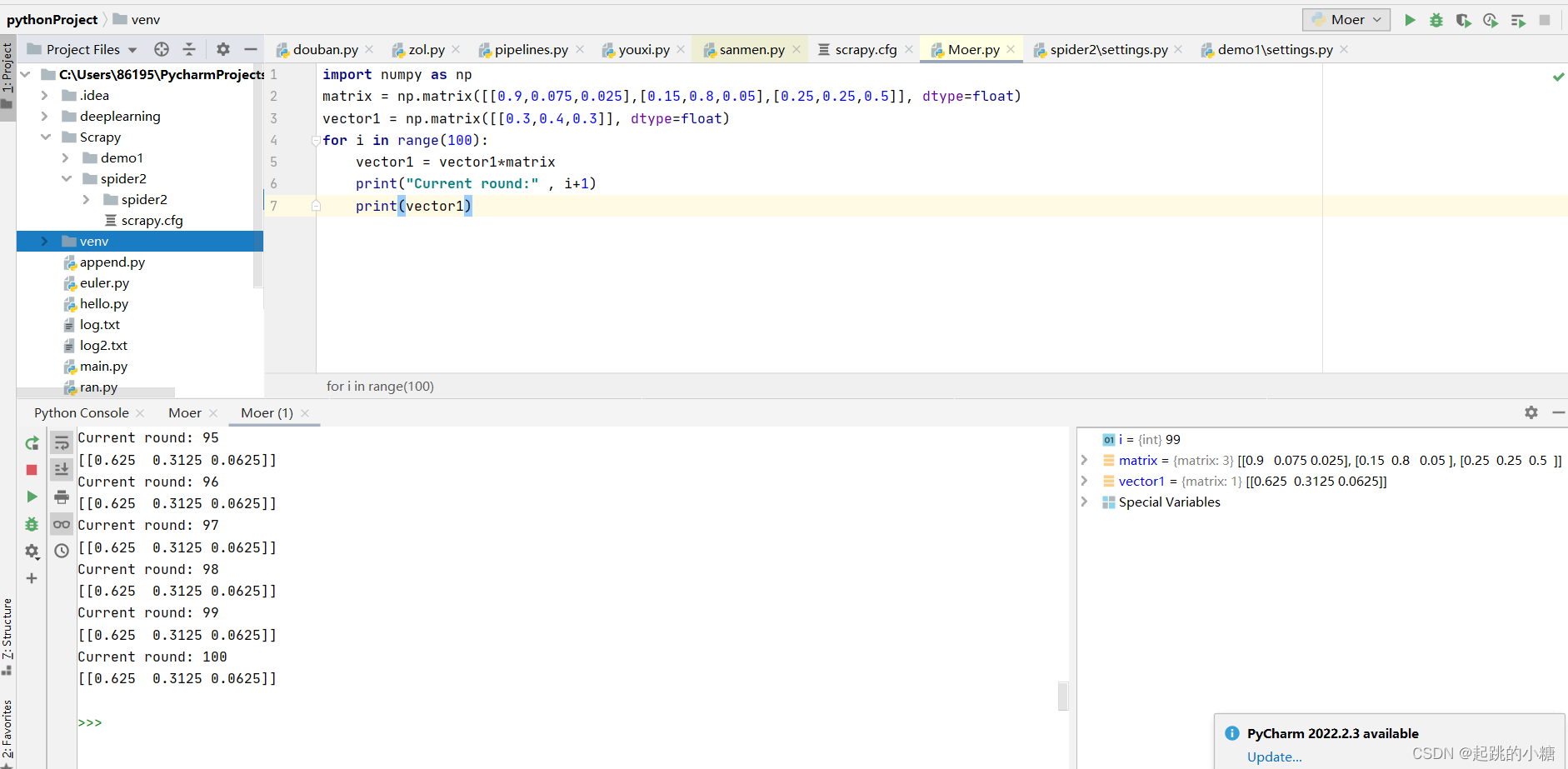
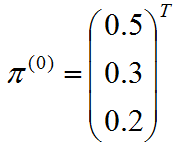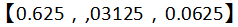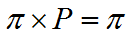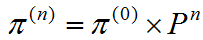1.概念及模型

马尔科夫链本质上是由满足马尔科夫性质的转移概率分布组成。

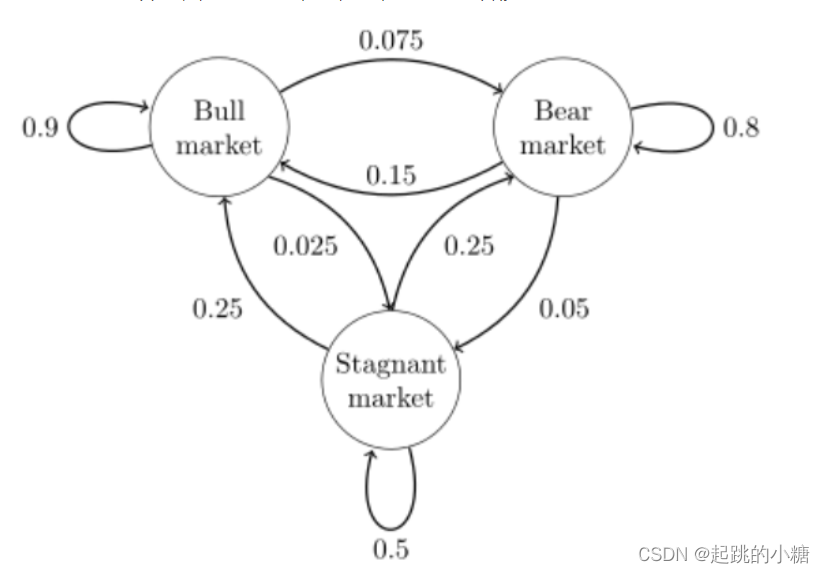
马尔科夫链是通过状态转移的概率分布体现的，称为马尔科夫链的转移矩阵。如果马尔科夫链有N个可能的状态，则转移矩阵的大小是N阶，矩阵的项（i,j）是状态i到状态j的转移概率，另外矩阵的每一行的转移概率和等于1，表示状态i的概率分布。

如下图，状态用圆表示，边表示状态的转移概率。

 经过多次状态转移后，状态的分布收敛于稳定的概率分布：

因此状态分布的收敛性与初始状态的分布无关，经过多次状态转移后，状态趋于平稳分布，方程式表示如下：

得到状态分布与状态转移的关系：

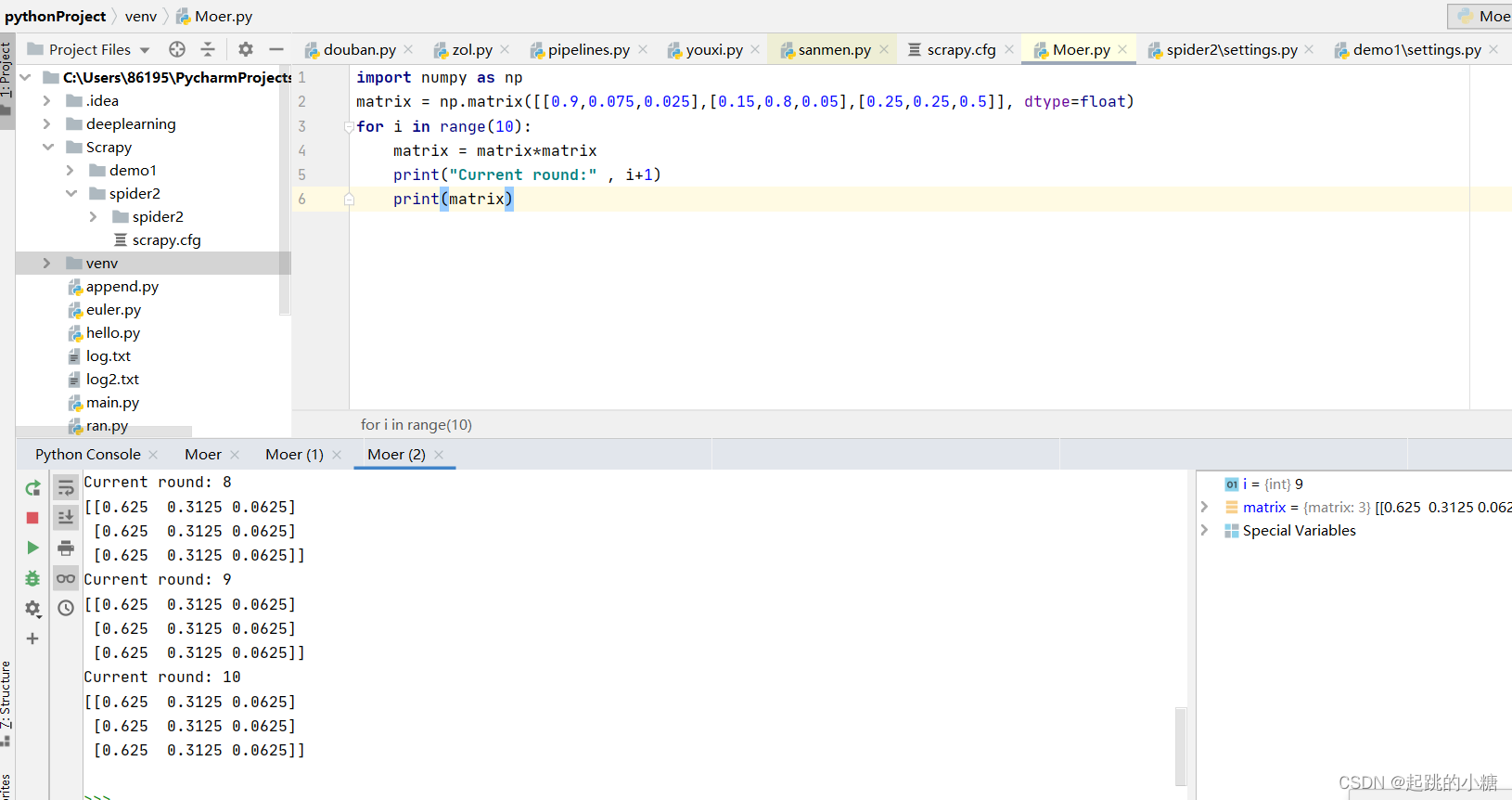
 2.性质及实现

假设概率分布为：[0.3,0.4,0.3],即30%概率的牛市，40%概率的熊盘与30%的横盘。然后这个状态作为序列概率分布的初始状态t0t0，将其带入这个状态转移矩阵计算t1,t2,t3...t1,t2,t3...的状态。

用[0.7,0.1,0.2]作为初始概率分布

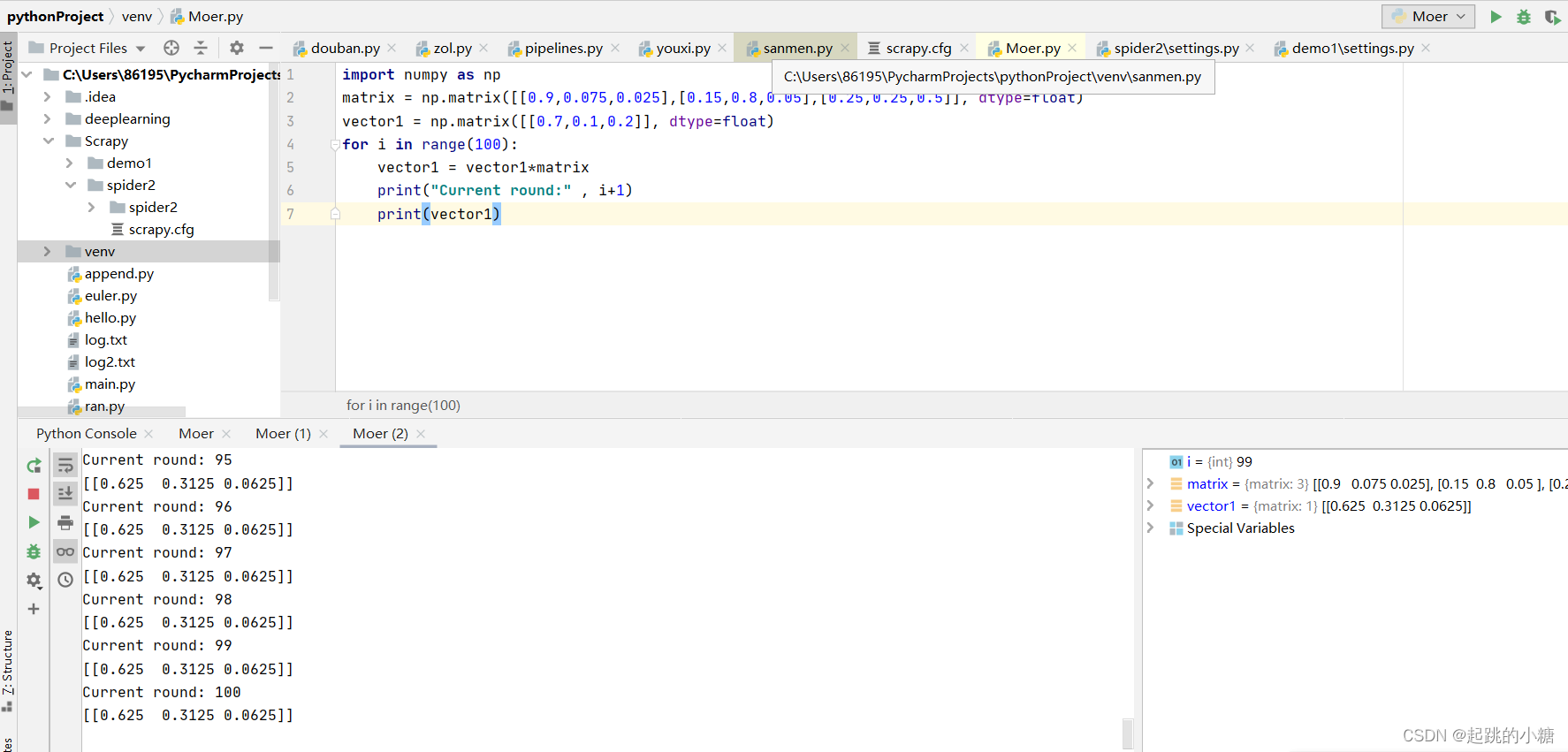
马尔科夫链模型的状态转移矩阵收敛到的稳定概率分布与我们的初始状态概率分布无关。不光是离散状态，连续状态时也成立。

对于一个确定的状态转移矩阵PP，它的n次幂PnPn在当n大于一定的值的时候也可以发现是确定的：