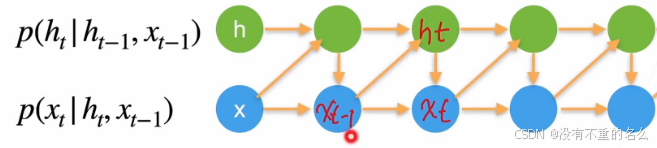
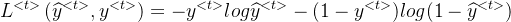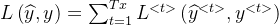循环神经网络RNN

潜变量自回归模型：

使用潜变量ht总结过去信息

Xt与ht、Xt-1相关

ht与ht-1和Xt-1相关

标准神经网络的不足：

输入和输出数据在不同例子中可能有不同的长度

一个像这样单纯的神经网络结构，它并不共享从文本不同位置上学到的特征：

①以前的特征输入是稳定的，即所有的特征域表达的内容是同一性质的；比如人名是一个特征域类别，其他的是其他类别，一旦他们交换位置，需要重新学习特征

②若神经网络已经学习到在位置1出现的“Harry”可能是人名的一部分，那么如果“Harry”出现在其他位置，有可能就无法成功识别

③在位置1学习到识别人名的能力，但是名字在位置2出现，那么2就无法识别

参数量巨大：

①输入网络的特征往往是one-shot或embedding向量，维度大

②输入网络的特征是一段序列，当序列长时，输入向量大

无法体现出时序的“前因后果”

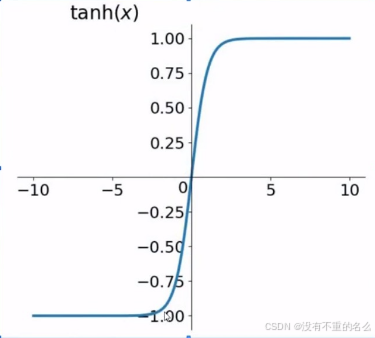
循环神经网络：

隐变量：可观察

浅变量：不可观察

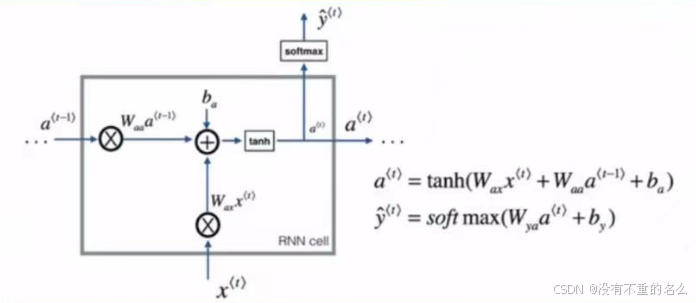
定义：

串联：后状态会受到前状态的影响，将前后关联

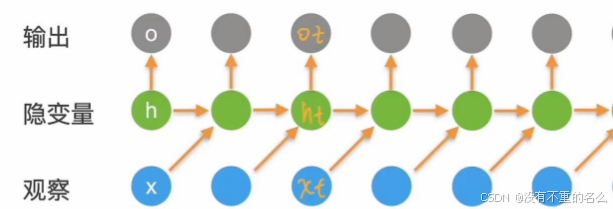
在T时刻的输出Ot是根据隐变量ht生成的，而ht使用的观察值是Xt-1

Ot用来匹配Xt的输入，但在生成Ot时看不到Xt；Xt是用来更新ht，使罗列到下一个单元；当前时刻的输出是预测当前时刻的观察，但是输出发生在观察之前

特点：

串联结构，体现出“前因后果”，后面的结果的生成，要参考前面的信息

所有的特征共享一套参数：

①面对不同的输入，能学到不同的相应的结果

②极大的减少了训练参数量

③输入和输出数据在不同例子中可以有不同的长度

计算损失：

比较Ot与Xt计算损失

单个时间步的损失函数：

$L^{<t> }\left ( \widehat{y}^{<t>},y^{< t> } \right )=-y^{< t> }log\widehat{y}^{<t >}-(1-y^{<t>})log(1-\widehat{y}^{<t>})$

整个序列的损失函数：将整个时间步的损失函数相加

$L\left ( \widehat{y},y \right )=\sum _{t=1}^{Tx}L^{< t> }\left ( \widehat{y}^{<t>},y^{< t> } \right )$

反向传播：

计算各层参数对损失的梯度，RNN中还要进行梯度的累加，进行权重的梯度更新

单个单元的梯度公式：

语言模型应用：

当前0时刻的输入做的输出作用在下一时刻

输入“你”，更新隐变量，预测“好”；观察到“好”，更新隐变量，输出下一个“，”

通过观察“你”的状态，将其转化为“好”的状态

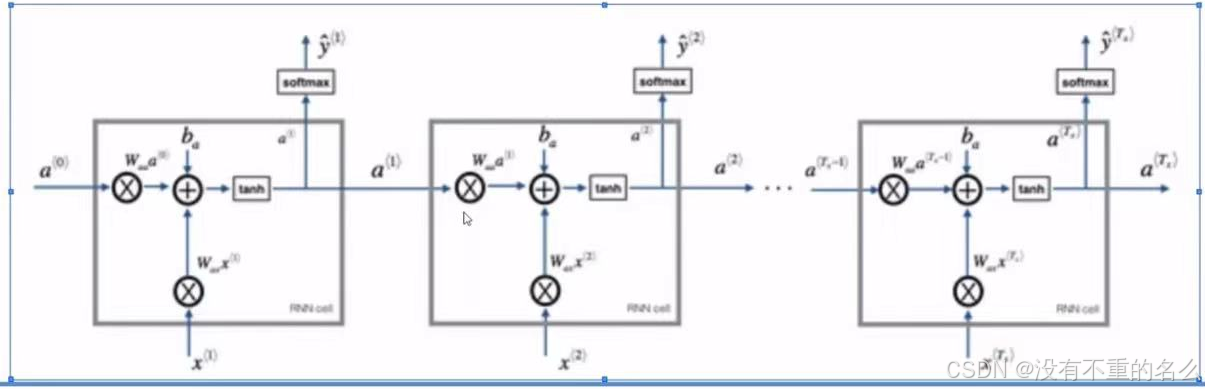
与MLP不同：

多了一个时间轴，使得和前一时刻的ht-1发生关系，而信息都存在h中

公式：

W代表权重，存储时序信息

输出还是使用隐藏状态

困惑度perplexity：

衡量一个语言模型（分类模型）的好坏可以用平均交叉熵

对一个序列做n次预测，也就是做n次分类，而对语言模型预测评价好坏就是取平均，n次交叉熵的平均值

若困惑度为k，则代表这一次预测的k个词都是有可能为预测值的

做指数可以让值更大，容易看出改进带来的优势

梯度裁剪：

背景：

当序列太长时，容易导致梯度消失，参数更新只能捕捉到局部依赖关系，无法再捕捉序列之间的长期关联或依赖关系。

迭代中计算这T个时间步上的梯度，在反向传播过程中产生长度为O(T)的矩阵乘法链，导致数值不稳定（数量很多的矩阵乘法会得到较大的值或较小的值）

RNN梯度消失手算过程：

作用：

梯度裁剪能有效预防梯度爆炸

梯度爆炸：导数值很大，或者出现了NAN

g的长度就是连乘的个数，超过theta就只保留theta个，不超过就全部保留

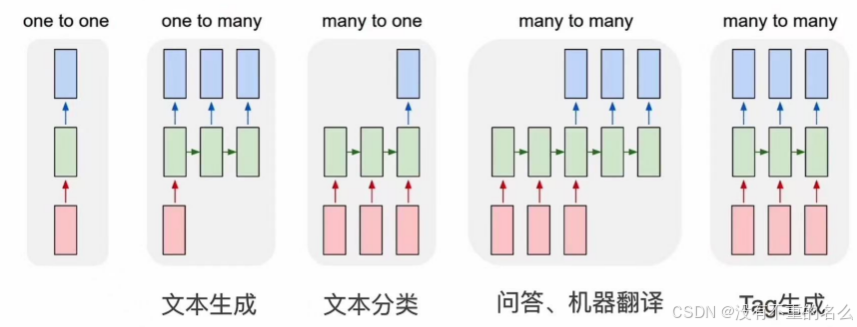
RNN的应用：

①one to one：最简单的一对一MLP，给一个样本输出一个label

②one to many：给一个词，生成一个词

③many to one：给一个序列，每一个时间t进入更新状态，在最后的时刻输出，得到完整的句子的分类

④many to many：给一个句子，先不做输出，在句子结束时开始输出，以问答和机器翻译的形式

⑤many to many：给一个句子，输出每一个词的tag

总结：

循环神经网络的输出取决于当下输入和前一时间的隐变量

应用到语言模型中时，循环神经网络根据当前词预测下一时刻词

通常使用困惑度来衡量语言模型的好坏