n皇后问题 C++

先上代码！

#include<iostream>
using namespace std;

const int N = 20;


int n;
bool row[N],col[N], dg[N], udg[N];
char g[N][N];

void dfs(int x, int y, int z)
{
    if (y == n) y = 0, x++; //判断y是否已经抵达边界，抵达后，x+1进行下一行
    if (x == n)
    {
        if (z == n) //皇后放完
        {
            for (int i = 0; i < n; i++)puts(g[i]); //输出棋盘
            cout << "\n";
        }

        return;
    }
    
    
    //放皇后

    if(!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n])//x轴,y轴，斜着的两条线都没有皇后时
    {
        g[x][y] = 'Q'; //放一个皇后
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true; //此时这些线被占住了
        dfs(x+1, 0, z + 1);//继续这个流程，x+1直接换行,从y = 0开始,z+1下一个皇后
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;//这叫回溯
        g[x][y] = '.'; //这叫回溯
    }

    //不放皇后, z不加1;y+1来像后面退格
    dfs(x, y + 1, z);

}



int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            g[i][j] = '.'; //造棋盘嗷
        }
    }

    dfs(0, 0, 0);

    return 0;
}

运算结果：

4
.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

5
Q....
..Q..
....Q
.Q...
...Q.

Q....
...Q.
.Q...
....Q
..Q..

.Q...
...Q.
Q....
..Q..
....Q

.Q...
....Q
..Q..
Q....
...Q.

..Q..
Q....
...Q.
.Q...
....Q

..Q..
....Q
.Q...
...Q.
Q....

...Q.
Q....
..Q..
....Q
.Q...

...Q.
.Q...
....Q
..Q..
Q....

....Q
.Q...
...Q.
Q....
..Q..

....Q
..Q..
Q....
...Q.
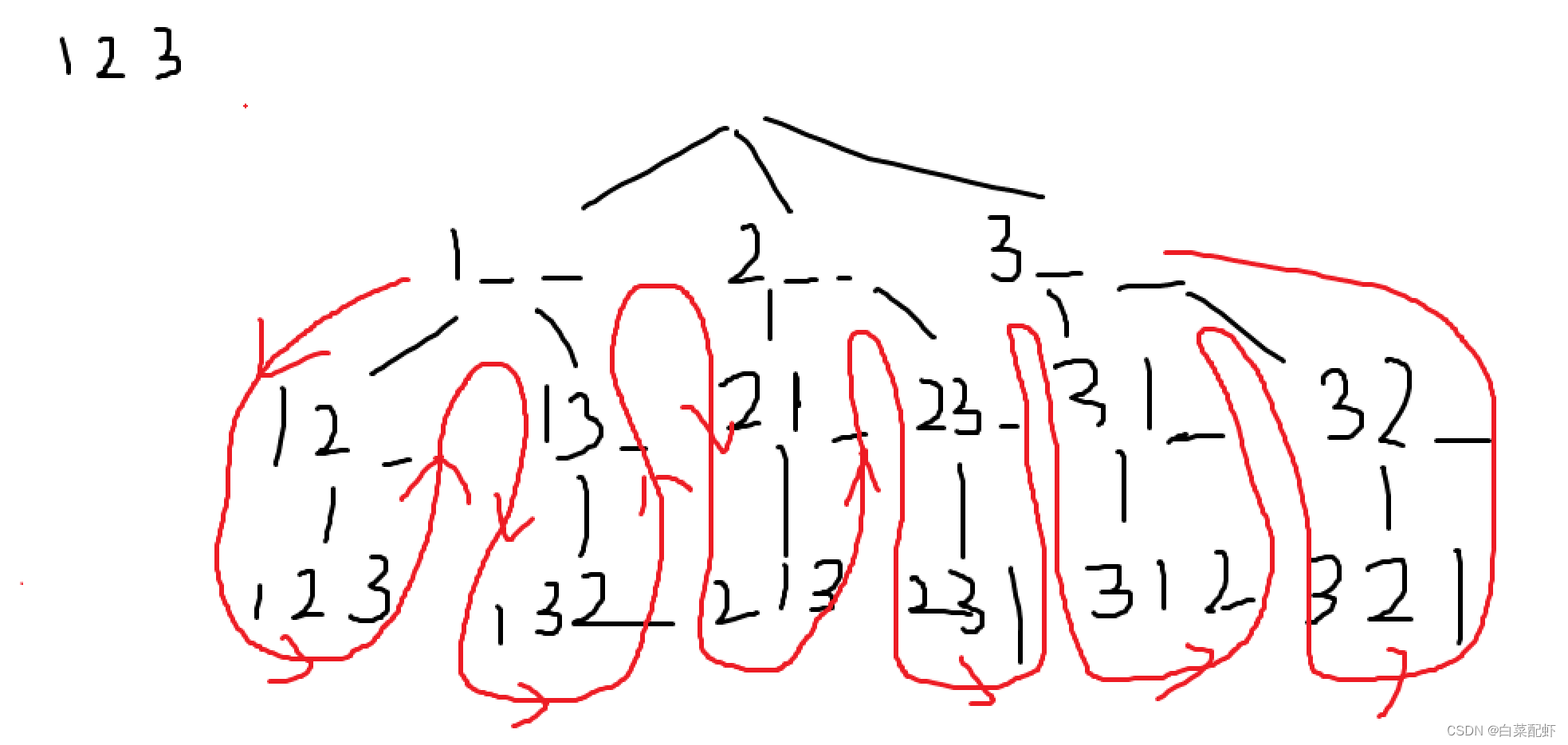
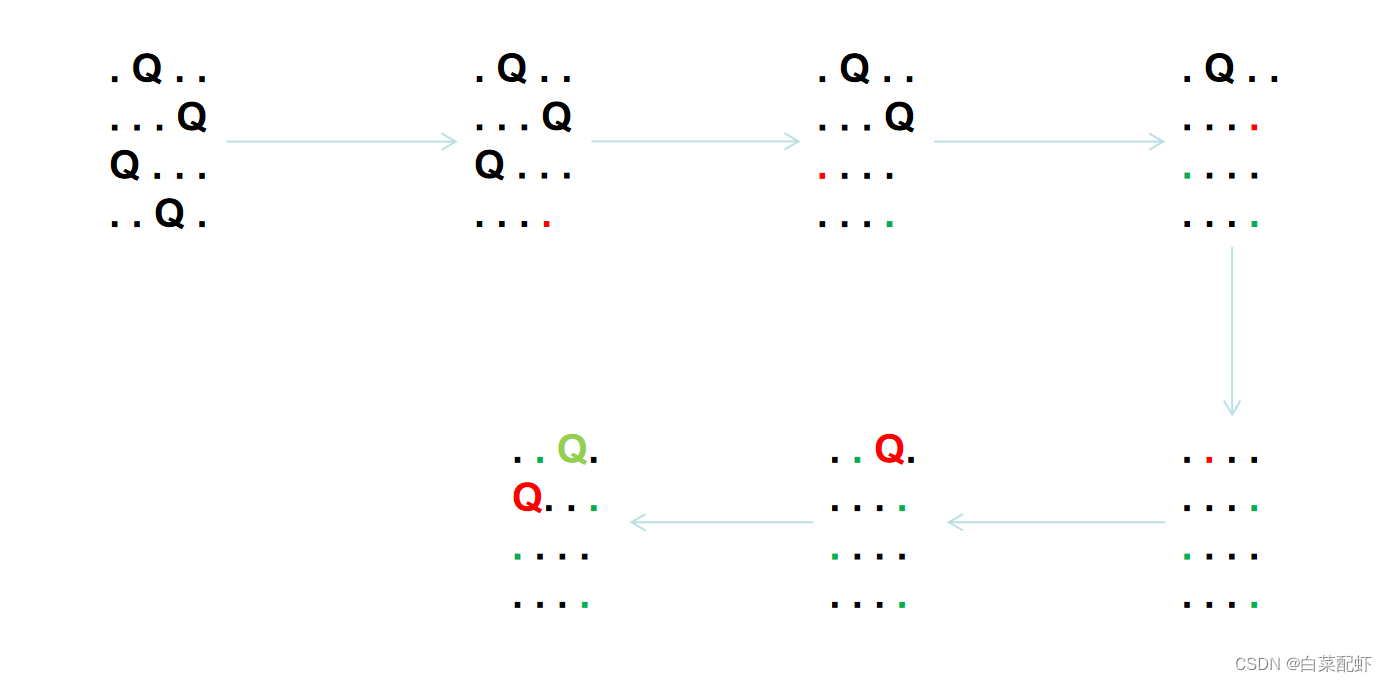
.Q...

是的，代码贼短，这个用到了深搜算法，DFS；理解了其实很简单；注释在代码里面有，主要讲一下回溯和剪枝,如图：

这道题就是问1 2 3所有排序；画图就是先在第一个位置填1，再在第二位置，第三个位置以次填2，3；然后你发现没数字可以填了，就可以回去一次1 2 3 - > 1 2 _，然后发现还是只能填3，就在回去一次 1 2 _ -> 1 _ _,然后可以填3；这就是回溯，这个代码我也整出来吧，可以和八皇后一起看一下：

#include<iostream>

using namespace std;

const int N = 10;

bool st[N]; //这个数有没有用过
int n;
int path[N];



void dfs(int u)
{
	if (u == n)
	{
		for (int i = 0; i < n; i++) cout << path[i] << " ";
		cout << "\n";
		return;
	}

	for (int i = 1; i <= n; i++)
	{
		if (!st[i])
		{
			path[u] = i;
			st[i] = true;
			dfs(u + 1);
			st[i] = false;
		}
	}
}



int main()
{
	cin >> n;

	dfs(0);

	return 0;
}

完毕，不懂就多看看……

算了，再给你们整个图，方便你们理解，文字描述就不写了，就是不断回溯的流程：

return后Q -> .，并往后退判断成不成立，不成立就继续回溯，然后直接回溯到第一行，第一行终于成立了，然后就继续了。（ !保姆级教程！）

这下真的完了

n皇后问题 C++

悦读