一、缺失值处理
- 删除缺失值:
data1=data.dropna()#丢弃缺失值
#dropna()删除缺失值所在行(axis=0)或列(axis=1),默认为 axis=0- 补全
import pandas as pd
import numpy as np
data = pd.DataFrame({
'name': ['Bob', 'Mary', 'Peter', np.nan, 'Lucy'],
'score': [99, 100, np.nan, 91, 95],
'class': ['class1', 'class2', 'class1', 'class2', np.nan],
'sex': ['male', 'fmale', 'male', 'male', 'fmale'],
'age': [23, 25, 20, 19, 24]
})
(1)均值填充
- 适用场景:数据整体极值差异不大时
- 举例:对成年男性身高的缺失值进行填充
#对data数据中的score进行均值填充
data['score'].fillna(data['score'].mean())
# 结果如下
0 99.00
1 100.00
2 96.25
3 91.00
4 95.00
(2)中位数填充
- 适用场景:数据整体极值差异较大时
- 举例:对人均收入进行填充(数据中含有高收入人群:如马总)
#对data数据中的score进行中位数填充 data['score'].fillna(data['score'].median()) # 结果如下 0 99.0 1 100.0 2 97.0 3 91.0 4 95.0
- 适用数据类型:字符类型|没有大小关系的数值类型数据
- 适用场景:大多数情况下
- 举例:对城市信息的缺失进行填充/对工人车间编号进行填充
- 代码示例:对
data数据中的class进行众数填充(注意:众数填充时要通过索引0进行取值,一组数据的众数可能有多个,索引为0的数据一定会存在)data['class'].fillna(data['class'].mode()[0]) # 结果如下 0 class1 1 class2 2 class1 3 class2 4 class1
- 适用场景:数据行与行之间具有前后关系时
- 举例:学年成绩排行中的某同学某科目成绩丢失
#代码示例:对data数据中的score进行前后数据填充 # 前文填充 data['score'].fillna(method='pad') # 后文填充 data['score'].fillna(method='bfill') # 前文填充结果 0 99.0 1 100.0 2 100.0 3 91.0 4 95.0 # 后文填充结果 0 99.0 1 100.0 2 91.0 3 91.0 4 95.0(5)自定义数据填充
- 适用场景:业务规定外的数据
- 举例:某调查问卷对婚后幸福程度进行调查,到那时很多人是未婚,可以自定义内容表示未婚人群
#代码示例:对data数据中的name进行自定义数据填充 data['name'].fillna('no_name') # 结果如下 0 Bob 1 Mary 2 Peter 3 no_name 4 Lucy(6)Pandas插值填充
-
适用场景:数据列的含义较为复杂,需要更精确的填充方法时
举例:对所有带有nan的数值列dataframe进行填充
说明:pandas中进行空值填充的方法为interpolate(),该方法的本质是使用各种数学(统计学)中的插值方法进行填充,其中包含最近邻插值法、阶梯插值、线性插值、B样条曲线插值等多种方法。data['score'].interpolate() # 结果如下 0 99.0 1 100.0 2 95.5 3 91.0 4 95.0(7)建模填充
- 适用场景:具有多种数据维度的场景
- 说明:可以选择不同的回归|分类模型对数据进行填充
- 注意:下面的例子中不考虑具体场景,只是用于举例
- 数值类型数据填充代码示例(线性回归):
-
from sklearn.linear_model import LinearRegression # 获取数据 data_train = data.iloc[[0, 1, 3]] data_train_x = data_train[['age']] data_train_y = data_train['score'] # 使用线性回归进行拟合 clf = LinearRegression() clf.fit(data_train_x, data_train_y) # 使用预测结果进行填充 data['score'].iloc[2] = clf.predict(pd.DataFrame(data[['age']].iloc[2])) - 字符类型数据填充代码示例(决策树):
from sklearn.tree import DecisionTreeClassifier
# 获取数据
data_train = data.iloc[[0, 1, 3]]
data_train_x = data_train[['age']]
data_train_y = data_train['class']
# 使用决策树进行拟合
clf = DecisionTreeClassifier()
clf.fit(data_train_x, data_train_y)
# 使用分类结果进行填充
data['class'].iloc[4] = clf.predict(pd.DataFrame(data[['age']].iloc[4]))[0]
二、异常值检测与处理
异常值检测
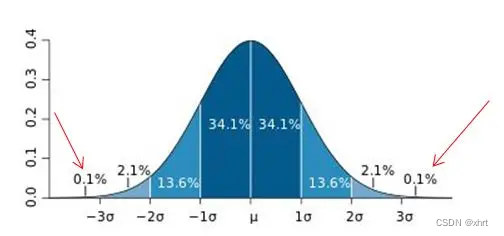
1、3∂原则
要求:数据服从或近似服从正态分布
在3∂原则下,异常值如超过3倍标准差,那么可以将其视为异常值。正负3∂的概率是99.7%,那么距离平均值3∂之外的值出现的概率为P(|x-u| > 3∂) <= 0.003,属于极个别的小概率事件。如果数据不服从正态分布,也可以用远离平均值的多少倍标准差来描述。
需要注意的是,3σ方法假设数据服从正态分布,因此在应用时要确保数据的分布近似于正态分布。如果数据不满足这个假设,其他异常值检测方法可能更合适。此外,3σ方法可能对极端值(outliers)不够敏感,因此在某些情况下可能会漏检一些异常值。因此,在实际应用中,通常需要结合其他方法进行异常值检测,以提高检测的准确性。
首先检验数据是否正态分布
# pvalue大于0.05则认为数据呈正态分布
from scipy import stats
mean = df['age'].mean()
std = df['age'].std()
print(stats.kstest(df['age'],'norm',(mean,std)))
异常值处理
# 选取小于3个标准差的数据
data = data[np.abs(df['age']- mean) <= 3*std]
如果数据不符合正态分布,也可以用远离平均值的多少倍标准差来筛选异常值。具体倍数看数据情况和业务需求
# 定义远离平均值4倍标准差为异常值
a = mean + std*4
b = mean - std*4
data = data[(data['Age'] <= a) & (data['Age'] >= b)]
或者定义为函数:
def three_sigma(s):
mu, std = np.mean(s), np.std(s)
lower, upper = mu-3*std, mu+3*std
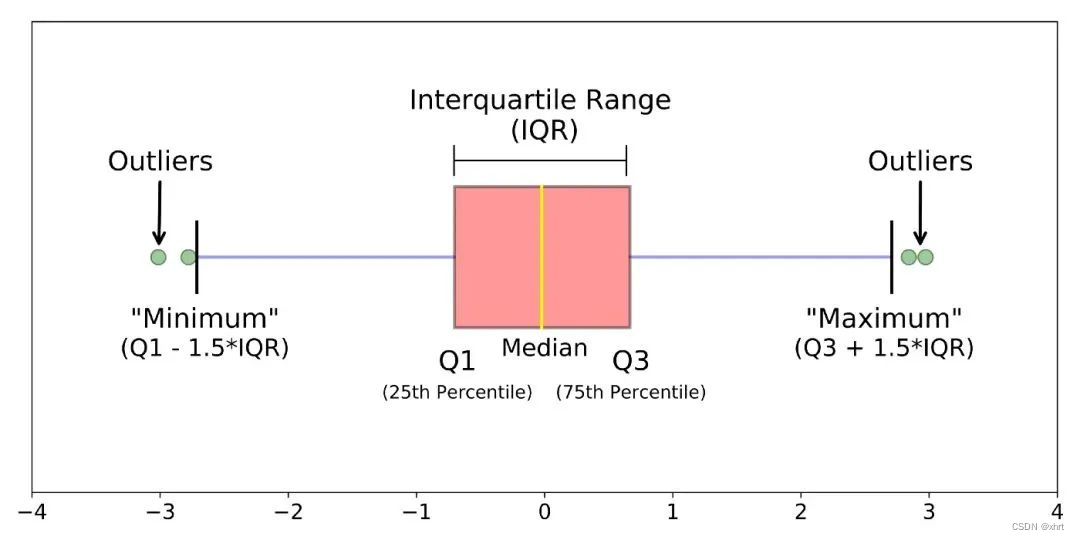
return lower, upper2、箱型图
利用箱型图的四分位距(IQR)对异常值进行检测,四分位距(IQR)就是上四分位与下四分位的差值。而我们通过IQR的1.5倍为标准,规定:超过上四分位+1.5倍IQR距离,或者下四分位-1.5倍IQR距离的点为异常值。
numpy的percentile方法。
data = np.array([2, 2, 3, 4, 5, 6, 7, 8, 1000])
Q1 = np.percentile(data, 25)
Q3 = np.percentile(data, 75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
outliers = np.where((data < lower_bound) | (data > upper_bound))
print("异常值的索引:", outliers)
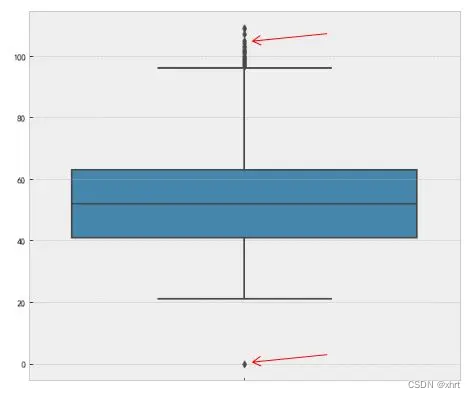
boxplot来实现:
f,ax=plt.subplots(figsize=(10,8))
sns.boxplot(y='length',data=df,ax=ax)
plt.show()
#或者用pandas自身的plot方法
data['Age'].plot(kind = 'box')
3、标准差的方法(Z-Score)
- 适用场景:用于检测连续型数据的异常值,数据应该服从正态分布或近似正态分布。
- Z-score为标准分数,测量数据点和平均值的距离,若A与平均值相差2个标准差,Z-score为2。当把Z-score=3作为阈值去剔除异常点时,便相当于3sigma。
-
import numpy as np from scipy import stats data = np.array([2, 2, 3, 4, 5, 6, 7, 8, 1000]) z_scores = np.abs(stats.zscore(data)) threshold = 3 outliers = np.where(z_scores > threshold) print("异常值的索引:", outliers)
Smoothed Z-Score
通过计算数据点与其周围数据点的标准差来识别异常值,从而将数据平滑化。计算过程如下:
-
计算滑动窗口内的均值和标准差: 首先,你需要选择一个滑动窗口大小,通常是一个时间窗口(例如,10天)。然后,对于每个数据点,计算在该滑动窗口内的均值(mean)和标准差(standard deviation)。
-
计算 Z-Score: 对于每个数据点,计算其与滑动窗口内均值的差值,然后除以滑动窗口内的标准差,得到 Z-Score。
-
平滑 Z-Score: 对计算得到的 Z-Score 序列应用一种平滑技术,例如指数移动平均(Exponential Moving Average,EMA)或简单移动平均(Simple Moving Average,SMA),以减少噪音和平滑数据。
-
设定阈值: 最后,根据平滑后的 Z-Score,你可以设定一个阈值来识别异常值。如果平滑后的 Z-Score 超过或低于阈值,那么该数据点就被认为是异常值。
对于时间序列数据和需要考虑噪音的情况,Smoothed Z-Score 可能更适合,而对于符合正态分布假设的数据集,Z-Score 通常足够用来检测异常值。
4、基于密度的方法(DBSCAN)
- 适用场景:适用于数据集中包含群集的情况,可以找出离群的数据点。
from sklearn.cluster import DBSCAN
import numpy as np
data = np.array([[2], [2], [3], [4], [5], [6], [7], [8], [1000]])
dbscan = DBSCAN(eps=0.5, min_samples=2)
labels = dbscan.fit_predict(data)
outliers = np.where(labels == -1)
print("离群值的索引:", outliers)
5、Isolation Forest(孤立森林):
- 适用场景:适用于高维数据和数据中包含多种类型的异常值。
from sklearn.ensemble import IsolationForest
import numpy as np
data = np.array([[2], [2], [3], [4], [5], [6], [7], [8], [1000]])
isolation_forest = IsolationForest(contamination=0.05)
labels = isolation_forest.fit_predict(data)
outliers = np.where(labels == -1)
print("离群值的索引:", outliers)
常值处理方法
- 删除含有异常值的记录:直接将含有异常值的记录删除;
- 视为缺失值:将异常值视为缺失值,利用缺失值处理的方法进行处理;
- 平均值修正:可用前后两个观测值的平均值修正该异常值;
- 不处理:直接在具有异常值的数据集上进行数据挖掘;
三、标准化
1. Min-max 标准化 (Min-max Scaling)
这种方法将原始数据线性转换到 [0,1] 范围内。适用场景包括:
- 当算法(如,神经网络)需要固定范围的输入时。
- 当数据的标准差较小或分布不均匀时。
- 在需要保持稀疏矩阵中零元素位置的情况下。
但是,Min-max标准化受异常值的影响较大,即如果数据集中存在离群点,会导致其他“正常”数据点的压缩。
2. z-score 标准化 (Z-score Normalization)
这种方法基于原始数据的均值(mean)和标准差(standard deviation)进行转换,结果数据的均值为0,标准差为1。z-score 标准化适用场景包括:
- 当数据的分布接近正态分布时。
- 在许多机器学习算法中,例如支持向量机、逻辑回归、和 k-均值聚类等,因为这些算法对输入特征的量级和分布敏感。
- 当需要比较来自不同尺度和单位的特征时。
z-score 标准化对异常值有更好的稳健性,因为它是基于数据的均值和标准差的。
应用选择:
- 数据分布:z-score 更适合正态分布的数据,而 Min-max 更适合非正态分布的数据。
- 算法需求:对于要求输入在固定范围内的算法,例如神经网络,Min-max 可能更合适;而对于受到特征量级影响较大的算法,例如 k-均值聚类,z-score 可能更合适。
- 异常值的影响:当数据集中存在异常值时,z-score 标准化可能是更好的选择,因为它对异常值的影响较小。