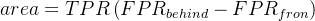机器学习基于Python实现PR曲线和ROC曲线

一、引言

PR曲线和ROC曲线是评估分类模型性能的重要工具。它们可以帮助我们在不同阈值下比较模型的性能，并选择最佳的阈值进行预测。这篇博客将介绍如何使用Python实现PR曲线和ROC曲线，并提供相应的示例代码。

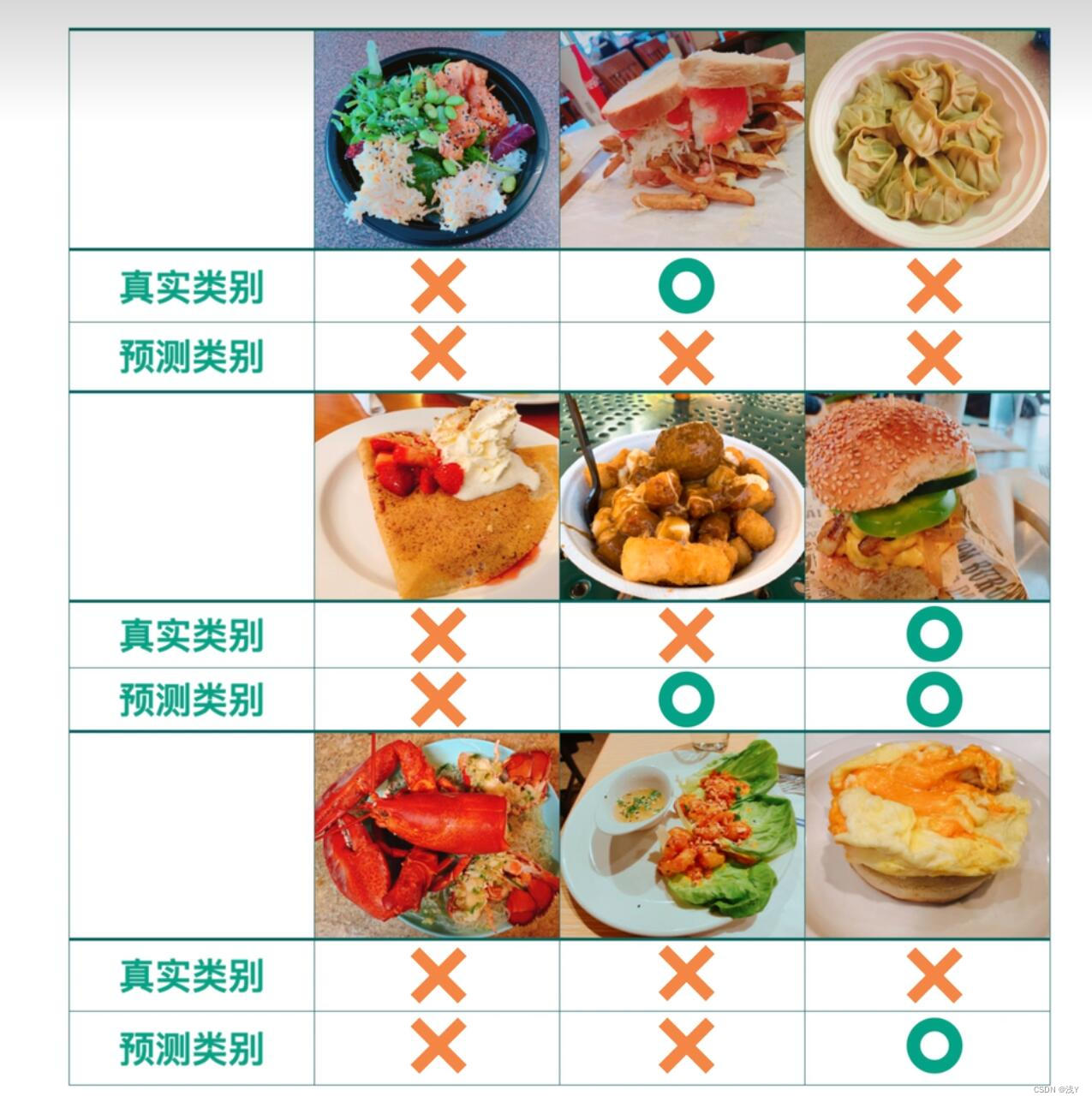
在介绍PR曲线之前，我们需要先了解几个概念。这里为了更加形象深刻地理解我们采用识别汉堡🍔的样例。为了判断一张图片是不是汉堡我们可以把照片扔进去一个分类器进行识别如下：

其中根据上面数据得到的预测和实际结果的对比我们做出了以下表格：

上面表格中的四个数组成的矩阵也就是我们需要理解的的混淆矩阵。

因此通过上述的案例我们学习到了几个名词：

真正例(True Positive，TP)：指正确分类成为正的样本数，实际为正，预测为正

伪反例(False Positive，FP): 指错误分类为正的样本数，实际为负，预测为正

伪反例(False Negative，FN):指错误分类为负的样本数，实际为正，预测为负

真反例(True Negative，TN):指正确分类为负的样本数，实际为负，预测为负

注意：以上的案例是比较简单的2x2的矩阵，根据实际中不同的案例可能会衍生出NxN的矩阵，同时也需要知道的是我们的目的是将预测正确的结果尽可能地变多，错误的尽可能变少从而使模型更加精准。

二、PR曲线

2.1、精确率、召回率和阈值

有了上面的基础我们能更好地理解这几个概念：

精确率（Precision）：在预测为正类的样本中，真正例的比例。

公式为：

$P=\frac{TP}{TP+FP}$

召回率（Recall）：在所有正类样本中，被正确预测为正类的比例。

公式为：

$R=\frac{TP}{TP+FN}$

其中

查准率P类似于，“检索出的信息中有多少比例是用户感兴趣的”；
查准率R类似于，“用户感兴趣的信息中有多少被检索出来了”；

阈值：假设我们有一个二分类问题，其中正类样本的数量为P，负类样本的数量为N。现在我们使用一个二分类模型对样本进行分类，得到了每个样本属于正类的预测概率yi。我们还需要设定一个阈值threshold∈[0,1]，将预测概率转换为二分类结果：当yi ≥threshold时，样本被判定为正类；否则，样本被判定为负类。

需要注意的是，精确率和召回率通常是相互矛盾的，即当我们提高精确率时，往往会牺牲召回率；而当我们提高召回率时，往往会牺牲精确率。因此，在实际应用中，我们需要权衡二者，并选择最佳的阈值来平衡精确率和召回率。

2.2、PR曲线的绘制

PR曲线是由精确率和召回率的点连成的线，横轴为Recall，纵轴为Precision，

在PR曲线中越右上凸越好，PR想要Precision 和Recall同时高。

1.首先需要按照正样本的概率将所有样本排序

2.其次我们需要从大到小设置不同的阈值并且得到不同的混淆矩阵来进行描点从而得到图片

具体的图片会在下面代码结果展示中给出。

2.3、PR曲线下的面积计算

PR曲线下面积是衡量二分类模型性能的重要指标之一，表示正例被正确预测的概率；以下提供了计算的一种常用方法：

首先，绘制出PR曲线。
将PR曲线划分成多个小矩形，每个小矩形的高度为Precision值，宽度为Recall的变化范围。
计算每个小矩形的面积： $area=precision*\left ( Recall_{behind}-Recall_{fron}\right )$ 指的是后点减去前点
对所有小矩形的面积进行累加，得到PR曲线下面积： $AUPR=\sum_{i=1}^{n}area_{i}$ ,其中nn为小矩形的数量。

以下是代码的实现：

# 计算PR曲线下的面积
pr_auc = np.trapz(precision[::-1], recall[::-1])

三、ROC曲线

3.1、真正率、假正率

与PR曲线类似，ROC曲线也是一种评估二分类模型性能的工具。在ROC曲线中，横轴是假正例率，纵轴是真正例率。定义如下：

真正例率（TPR）：在所有正类样本中，被正确地判定为正类的比例。

公式为：

$TPR=\frac{TP}{TP+FN}$

假正例率（FPR）：在所有负类样本中，被错误地判定为正类的比例。

公式为：

$FPR=\frac{FP}{TN+FP}$

3.2、ROC曲线的绘制

与PR曲线类似，我们可以遍历一系列阈值，计算出每个阈值下的FPR和TPR，并将其绘制成ROC曲线，因此不过多赘述。

3.3、ROC曲线下的面积计算

ROC曲线下面积（ AUC）是衡量二分类模型性能的重要指标之一，表示模型在不同阈值下真阳性率（TPR）与假阳性率（ FPR）之间的权衡。

计算ROC曲线下面积的方法有多种，其中一种常用的方法是通过对ROC曲线上的点进行数值积分得到。下面是计算AUC的一种常见方法：

首先，绘制出ROC曲线。
将ROC曲线划分成多个小矩形或梯形，每个小矩形/梯形的高度为TPR，宽度为FPR的变化范围。
计算每个小矩形/梯形的面积，即当前点的TPR乘以（后一点和前一点FPR之差）： $area=TPR×\left ( FPR_{behind}-FPR_{fron} \right )$
对所有小矩形/梯形的面积进行累加，得到ROC曲线下面积： $AUC=\sum_{i=1}^{n}area_{i}$ ，其中n为小矩形的数量

代码实现：

# 计算PR曲线下的面积
pr_auc = np.trapz(precision[::-1], recall[::-1])

四、示例代码

导入和读取数据集并作出训练和测试集:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

# 加载数据集
cancer = load_breast_cancer()

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=42)

# 假设我们已经有了模型对测试集进行了预测，并得到了预测概率值
# 这里使用随机生成的示例数据
y_scores = np.random.rand(len(y_test))

计算pr曲线和获得面积并且绘制：

# 计算PR曲线
precision, recall, thresholds = [], [], []
# 遍历不同阈值，计算精确率和召回率
for threshold in np.linspace(0, 1, num=100):
    # 根据阈值将预测概率转换为类别
    y_pred = np.where(y_scores >= threshold, 1, 0)

    # 计算精确率、召回率和阈值
    tp = np.sum(np.logical_and(y_pred == 1, y_test == 1))
    fp = np.sum(np.logical_and(y_pred == 1, y_test == 0))
    fn = np.sum(np.logical_and(y_pred == 0, y_test == 1))

    if tp + fp == 0:
        precision.append(0)
    else:
        precision.append(tp / (tp + fp))

    if tp + fn == 0:
        recall.append(0)
    else:
        recall.append(tp / (tp + fn))

    thresholds.append(threshold)

# 计算PR曲线下的面积
pr_auc = np.trapz(precision[::-1], recall[::-1])

# 绘制PR曲线
plt.figure()
plt.plot(recall, precision, lw=2, color='navy', label='PR curve (AUC = %0.2f)' % pr_auc)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.title('Precision-Recall curve')
plt.legend(loc="lower right")
plt.show()

计算roc曲线并绘制

# 计算ROC曲线
fpr, tpr, thresholds = [], [], []
# 遍历不同阈值，计算假正率和真正率
for threshold in np.linspace(0, 1, num=100):
    # 根据阈值将预测概率转换为类别
    y_pred = np.where(y_scores >= threshold, 1, 0)

    # 计算真正率、假正率和阈值
    tp = np.sum(np.logical_and(y_pred == 1, y_test == 1))
    fp = np.sum(np.logical_and(y_pred == 1, y_test == 0))
    tn = np.sum(np.logical_and(y_pred == 0, y_test == 0))
    fn = np.sum(np.logical_and(y_pred == 0, y_test == 1))

    fpr.append(fp / (fp + tn))
    tpr.append(tp / (tp + fn))
    thresholds.append(threshold)

# 计算ROC曲线下的面积
roc_auc = np.trapz(tpr[::-1], fpr[::-1])

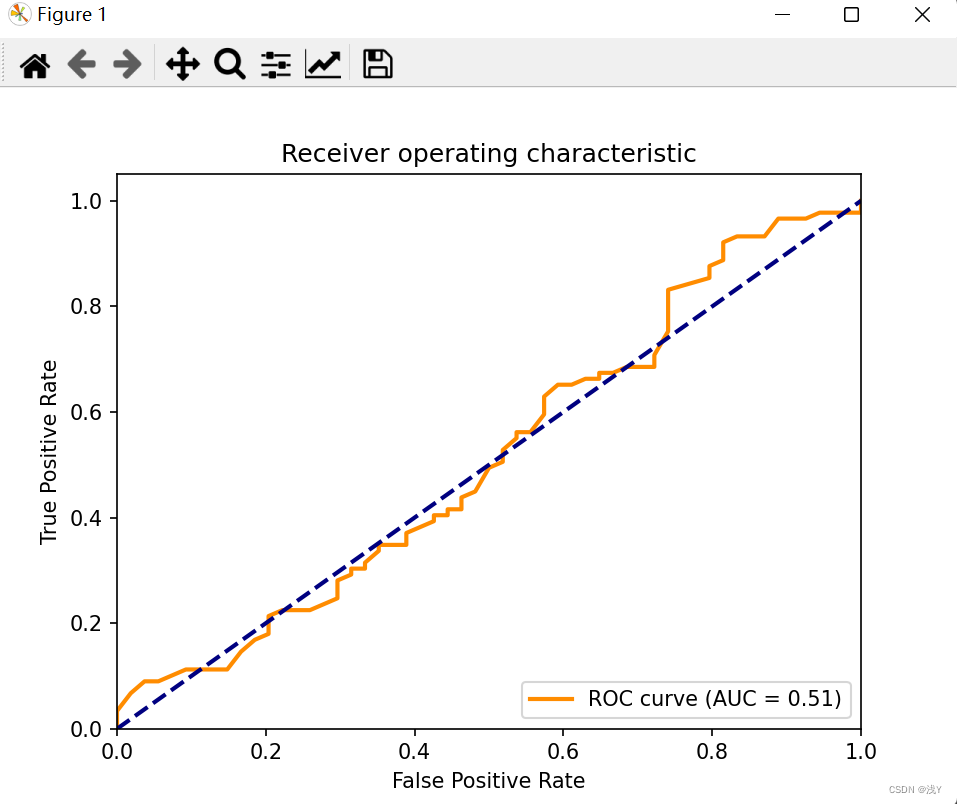
# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr, lw=2, color='darkorange', label='ROC curve (AUC = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.title('Receiver operating characteristic')
plt.legend(loc="lower right")
plt.show()

上述代码的实现都是根据公式来获得的

以下是运行结果的截图：

五、实验中遇到的错误和注意事项

由于最开始使用的数据集是多分类问题的，但是因为precision_recall_curve函数只支持二分类问题，所以会报错，后面经过资料查询发现需要使用OneVsRestClassifier对分类器进行包装，它可以将多分类问题转换为多个二分类子问题，问题得到解决。但是最快的解决办法是直接换个二分类的数据集就行咯。

六、小结

PR曲线和ROC曲线是评估二分类模型性能的重要工具。通过绘制PR曲线和ROC曲线，我们可以比较不同阈值下模型的性能，并选择最佳的阈值进行预测。本次博客我先从最基础的逻辑实现开始介绍，一步步深入最后通过代码进行实现。