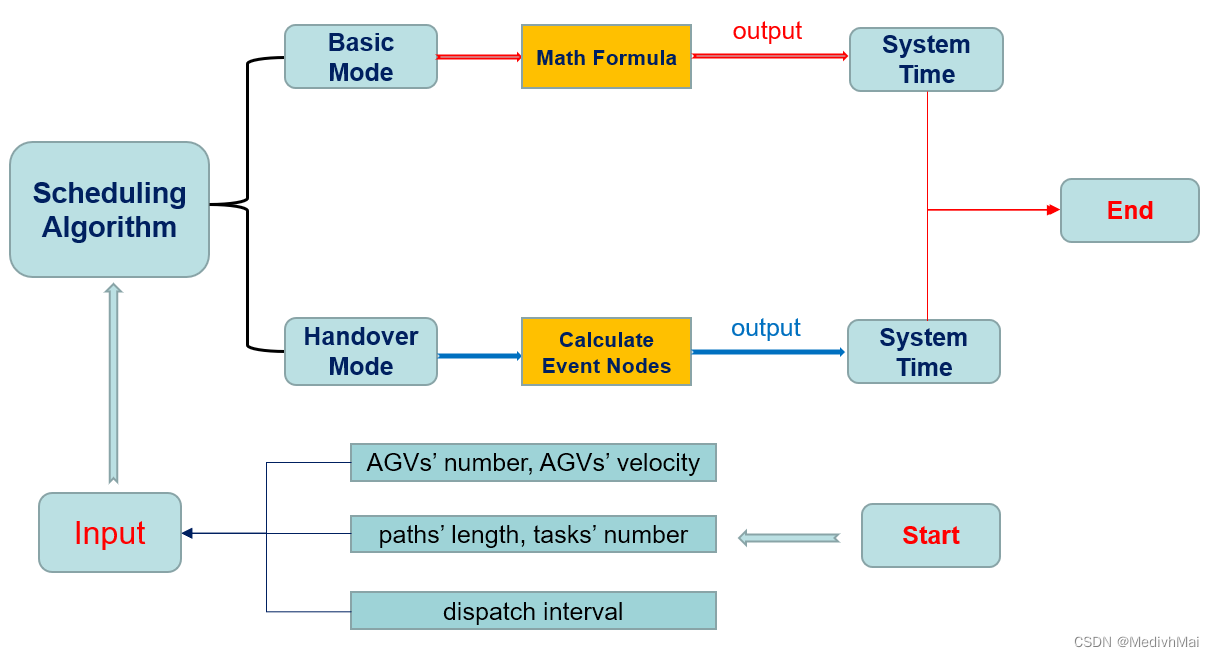
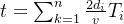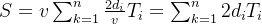AGV调度算法

AGV调度算法的目标是在指定原点向多条路径进行调度AGV派送任务。

如何用更快、成本更小地调度AGV？当变量足够多、情况足够复杂时, 很难从数学的角度找到一个通式或是最优解。本文主要探讨AGV调度算法的两种模式——basic模式和handover模式。

Basic模式

Basic模式指在一条路径上仅用一辆AGV进行调度, 是一种最简单的模式并且可以根据参数给出一个普遍的数学公式求解系统的运行时间：

$t=\sum_{k=1}^{n} \frac{2d_{i}}{v}T_{i}$

并且可由此得到AGV运动总距离：

$S=v\sum_{k=1}^{n} \frac{2d_{i}}{v}T_{i} = \sum_{k=1}^{n}2d_{i}T_{i}$

代码实现

已实现, 套公式即可。

Handover模式

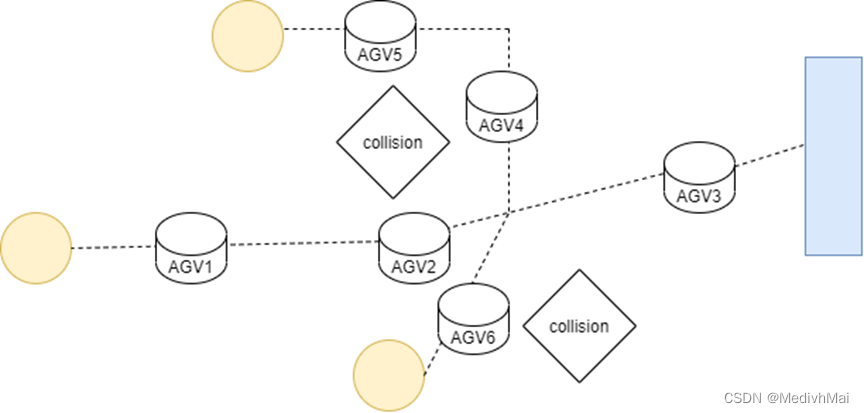
Handover模式指对任意路径的AGV调度数量无上限, 且在路径上的碰撞认定为任务的交接。交接完成后运行方向改变。

在现实中根据任务不同, 交接时间也不相同。当然, 本文主要讨论给定条件与参数的Handover模式, 只需要考虑交接时间平均值, 即交接时间固定. 以后研究实时AGV调度时,会考虑灵活交接时间的Handover情况。

当变量足够多，情况足够复杂时，很难得到一个普遍的数学公式。

本文首先从交接时间为0的理想情况入手, 此模式称为理想Handover模式。

理想Handover模式为Handover模式的极限情况。

理想Handover模式的特例

在理想情况下, 当系统有足够数量的AGV，满足为可连续派发AGV的特例时, 可给出一个数学公式计算系统运行时间：

$t=max\left \{ T_{1} t_{0} + \frac{2d_{1}}{v}, (T_{1}+T_{2})t_{0})+ \frac{2d_{2}}{v},....., t_{0}\sum_{k=1}^{i}T_{i}+ \frac{2d_{i}}{v},....., t_{0}\sum_{k=1}^{n}T_{n}+ \frac{2d_{n}}{v} \right \}$

可用归纳法证明,

调度优先级的数学归纳法证明：

结论1: 无交接时间情况下, 每条路各存在一个任务时, 满足调度优先级原则。(调度优先级原则：路径越长优先级越大)

首先声明：此情况为系统可调度的车辆足够多，只需要证明车辆够的情况就等价于证明了车辆不够的情况。

设AGV速度为v, 调度间隔为T

1.首先证明存在两条路径的情况

设d1<=d2

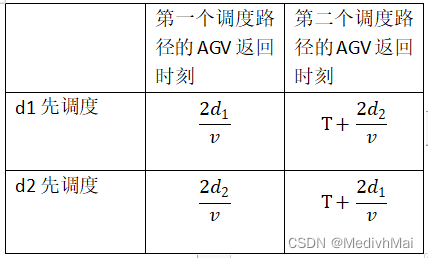
易知，两条路径的情况共有2种调度顺序。

d1 -> d2

d2 -> d1

从图表中可知, 若d1先调度, 则系统的最终返回时间必为 $T+\frac{2d_{2}}{v}$ 。此时间大于d2先调度情况下的任何返回时刻。

所以调度顺序应为d2 -> d1

因此，当只有两条路径时，路径越长调度优先级越大.........①

2.下面证明存在三条路径的情况。

设d1<=d2<=d3

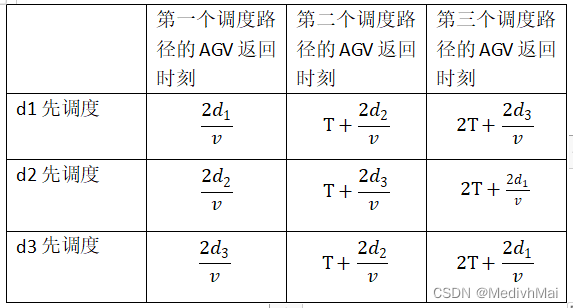
易知，三条路径的情况共有6种调度顺序:

d1 -> d2 -> d3

d1 -> d3 -> d2

d2 -> d1 -> d3

d2 -> d3 -> d1

d3 -> d1 -> d2

d3 -> d2 -> d1

首先我们固定第一条路径, 根据结论①可知, 剩下的两条路径中长路径先调度.

因此, 三种路径的情况化简为3种调度顺序：

d1 -> d3 -> d2

d2 -> d3 -> d1

d3 -> d2 -> d1

所以d1先调度的时间必然大于d3先调度的. 所以d1不可能先调度。

所以，顺序应为d3 -> d2 -> d1

综上所述, 当存在三条路径时，满足路径越长调度优先级越大。

下面证明当存在n条路径时的情况：

设d1<=d2<=d3....<=dn。

当存在2, 3条路径时，满足调度优先级原则

假设存在(n-1)条路径时, 满足调度优先级原则。

当存在n条路径时:

同样固定第一个调度路径, 根据(n-1)路径下的假设，同理将各种调度顺序化简为:

d1 -> dn -> dn-1 -> ...... ->d3 -> d2

d2 -> dn -> dn-1 -> ...... ->d2 -> d1

d3 -> dn -> dn-1 -> ...... ->d2 -> d1

.......................

dn-1 -> dn -> dn-2 -> ...... ->d2 -> d1

dn -> dn-1 -> dn-2 -> ...... ->d2 -> d1

除了dn路径先调度的情况以外, 其他所有情况的第二次调度的返回时刻均为（ $(T+\frac{2d_{n}}{v})$ ）

将其他调度情况的所有第二项开始与dn先调度情况的第一项开始对比：

只需要将其他情况与dn先调度的情况一一对比即可。

下面对比di与dn两条路的情况。

理想Handover模式

现在考虑任何情况下的理想Handover模式。根据经验判断, 因为Handover模式允许多任务并行调度, 所以时间效率会比Basic模式高很多(理想Handover模式下达到极限值)。

但是有一个问题Handover模式需要考虑, 而Basic模式不用考虑。即对不同长度、不同任务数量、不同调度时间且不同AGV数量的路径该如何调度？

如果要严谨地回答此问题, 需要用一个个结论进行推导。但从直觉上, 应先给较长的路径进行调度任务。比如有两条路径各有一个任务且有两个AGV, 因为调度间隔的存在, 如果先给短路径调度, 会导致与先给长路径调度相比, 系统时间可能会多一个调度间隔的时间。

因此, 此情况下长路径优先级更高。

据此推想：对于任意多条路径、每个路径任意多任务、有任意多个AGV、任意调度时间间隔,都满足路径越长优先级越高？

有表格中可知, 从第(n-i+1)个间隔以后, 调度顺序一样，因此每一项都相同。

只需要比较前(n-i)项即可。

从第2项开始到第(n-i)项, di先调度情况下的项数的返回时刻都大于等于dn先调度情况下的项数。

最后观察第一项，di先调度的第二项(T+An) > An, 因此dn先调度返回时刻的第一项同样小于di先调度中返回时刻的一项。

综上所述，dn先调度情况下的返回时刻中的每一项，在di先调度情况下的返回时刻中都存在一项，大于或等于这一项。

因此，n条路同样满足调度优先级原则。

证毕。

结论2: 无交接情况下，系统的时间与各种事件时刻均不受碰撞的影响

因为交接时间为极限情况0的特性, 一个AGV往返的时间始终为常数2d/v, 因为有AGV与之碰撞，导致其方向相反, 但是情况与两AGV碰撞后方向不变的情况等价(即任务会传递, 但方向不变)，两种情况所有的事件节点时刻一致。所以，我们认为一个AGV往返一次的事件始终为常数2d/v，即系统的时间、时刻均与碰撞无关。

结论2: 无交接情况下，系统的时间与各种事件时刻均不受碰撞的影响

理想Handover模式路径优先级的“不严谨”证明

目标：最大程度降低系统运行时间。

基本原理：任意条路径上, 单个任务的总运送时间不变。

推论：任意一条路径都有N个任务, 路径越长优先级越大。

证明：

可用归纳法进行证明。

结论：对于任意路径、任意任务数量, 路径越长优先级越大。

证明：

当所有路径的任务数量的情况不相同时, 根据基本原理, 任何情况下(AGV无交接时间), 单个任务的运送时间不会改变。问题等价于将N个任务转化为N个路径上都只有1个任务的情况。所以根据推论1, 依然按照路径从高到底进行调度AGV。

比如: 有路径d1, d2, d3各有任务2, 1, 3。则根据结论2, 问题等价于2条路径d1, 1条路径d2, 3条路径d3，并且这6条路上各有1个任务。

推论1:

当每条路存在m个任务时，同样满足调度优先级原则。

证明:

设有n条路径，共有mn条路

根据结论3，此问题等价于, mn条路每条路都有一个任务。

根据调度优先级原则, 长路径优先调度。

因此, 当每条路存在m个任务时，同样满足调度优先级原则。

推论2:

当任意条路径存在任意多任务时，同样满足调度优先级原则。

证明:

根据结论3，问题等价于有相同任务数量的路径数量。因此每条路各一个任务, 且路径长度等于原任务所在的路径的长度。

因此根据结论1，满足调度优先级原则。

因为问题等价，所以每条路存在任意多任务时，同样满足调度优先级原则，

根据推论2，在无交接情况下，任何情况下都满足调度优先级原则。即路径越长，调度优先级越大，以满足系统运行时间最短。

理想Handover模式代码实现

现在我们知道了路径越长调度的优先级越大。该考虑如何实现了。

本文给出两种理想Handover模式算法的代码。一种是根据以基本原理为基础的整体式计算法, 一种是根据事件节点进行时间推进的节点式计算法。

整体式计算法

因为是一种理想模式下才存在的讨巧算法，代码规则简单。存在交接时间时, 此方法失效。

此代码尚有bug，思路根据基本原理每条路径每个任务运送时间不变，知道思路即可。

代码:

import java.util.ArrayList;
import java.util.Scanner;

class AGV1 {
    ArrayList<Double> list = new ArrayList<>();
}

public class AGV调度算法NPathHandover模式整体法 {
    static double time = 0;
    static int n;
    static int used = 0;
    static double T;
    static double v;
    static double[] path;
    static int[] Task;
    static double Interval;
    static ArrayList<AGV1> AGVlist = new ArrayList<>();  //记录过去路径上AGV的返回时间


    public static void main(String[] args) {
        ParameterInput();
        CallHandover();
        System.out.println("最终时间t为:");
        System.out.println(time);
    }

    public static void CallHandover() {
        for (int i = 0; i < path.length; i++) {
            Handover(i);
        }
        double max = 0;
        for (int i = 0; i < AGVlist.size(); i++) {
            for (int j = 0; j < AGVlist.get(i).list.size(); j++) {
                double temp = AGVlist.get(i).list.get(j);
                if (temp > max) {
                    max = temp;
                }
            }
        }
        time = max;
    }

    public static void Handover(int index) {
        int dispatched = 0;
        AGV1 agv = new AGV1();
        double backTime = 2 * path[index] / v;
        if (index == 0) {
            agv.list.add(backTime);
            dispatched++;
            used++;
        }
        while (dispatched < Task[index]) {
            if (used < n) {
                dispatched++;
                used++;
                time += T;
                agv.list.add(time + backTime);
            } else {
                int a = -1;
                int b = -1;
                double min = Integer.MAX_VALUE;
                for (int i = 0; i < AGVlist.size(); i++) {
                    AGV1 temp = AGVlist.get(i);
                    for (int j = 0; j < temp.list.size(); j++) {
                        if (temp.list.get(j) < min) {
                            a = i;
                            b = j;
                            min = temp.list.get(j);
                        }
                    }
                }
                if (min <= time + T) {
                    time += T;
                } else {
                    time = min;
                }
                dispatched++;
                AGVlist.get(a).list.set(b, time + backTime);
            }
        }
    }

    public static void ParameterInput() {
        Scanner sc = new Scanner(System.in);
        System.out.println("输入AGV的数量");
        n = sc.nextInt();
        System.out.println("请输入AGV的运动速度:");
        v = sc.nextDouble();
        System.out.println("输入AGV派发间隔");
        T = sc.nextDouble();
        Interval = T;
        System.out.println("输入路径数量");
        int PathNum = sc.nextInt();
        path = new double[PathNum];
        Task = new int[PathNum];
        System.out.println("输入每条路径的长度");
        for (int i = 0; i < PathNum; i++) {
            path[i] = sc.nextDouble();
        }
        System.out.println("输入每条路径的任务数量");
        for (int i = 0; i < PathNum; i++) {
            Task[i] = sc.nextInt();
        }
    }
}

节点式计算法

节点式计算法, 顾名思义即模拟整个系统所有AGV的运动状态，是一种代码上较为繁琐复杂的算法。

首先研究单一路径下(1-Path Ideal Handover Mode)的节点式计算法

1-Path Ideal Handover Mode

三种事件节点:

1. 常规碰撞节点

常规碰撞节点, 指发生在路径上的AGV碰撞。若有任务时, 碰撞的两个AGV会交换任务并各自朝反方向运动。

2. 边界碰撞节点

边界碰撞节点, 指两个发生在边界的节点, 一个为AGV与起点的碰撞，一个为AGV与终点的碰撞。

3. 调度间隔节点

调度间隔节点, 指当前时刻满足调度间隔, 若有任务派发新的AGV进行运送。若有任务, 无AGV则会等待起点的边界碰撞节点。

代码

import java.util.*;

public class AGV调度问题handover模式_单一路径 {
    static int n; //number of the AGV
    static int TaskA; //number of the task A,B,C respectively.
    static double ta; //tc means the transmission time, and ta means the departure interval of AGV.
    static double v; //the speed of AGV.
    static double d1;    //the distance between origin and A,B,C respectively.
    static int used = 0;        //记录已投入使用的AGV数量为used,需要注意的是可以用ueed表示当前使用的最大AGV的车号.
    static double t = 0;         //记录已运行的时间
    static int completed = 0;    //已完成的任务
    static double currInterval = 0;    //距离上次派出AGV的时间间隔
    static HashMap<Integer, Integer> state = new HashMap<>();
    //第一位表示车号，第二位表示方向.-1为返回，1为前进.
    static ArrayList<Double> list = new ArrayList<>();
    //记录正在路径上的车的往返状态和具体位置.

    public static void main(String[] args) {
        OneDestination1();
        Handover();
        System.out.println("最终时间t为:");
        System.out.println(t);
    }

    //采取的思路是：已间隔时间推进系统时间的进步，即每次调用一次"PreSolution"时间就前进ta秒.
    public static void Handover() {
        while (completed != TaskA) {
            //定义事件节点
            double nodeTime = ta - currInterval;
            //没有车的情况
            if (used == 0) {
                t += ta - currInterval;
                currInterval = 0;
                state.put(0, 1);
                list.add(0.0);
                used++;
                nodeTime = ta - currInterval;
            }
            //无可用AGV且时间满足调度间隔时,
            if (used == n && nodeTime == 0) {
                nodeTime = Integer.MAX_VALUE;
            }

            //left=-1意思为终点位置, right=used意思为原点.
            int left = -1, right = used;

            //2个边界碰撞节点
            //边界碰撞节点-终点
            double temp = (d1 - list.get(0)) / v;
            if (state.get(0) == 1 && temp < nodeTime) {
                nodeTime = temp;
                left = -1;
                right = 0;
            }

            //边界碰撞节点-起点
            double temp2 = list.get(used - 1) / v;
            if (state.get(used - 1) == -1 && temp2 < nodeTime) {
                if (temp2 < nodeTime) {
                    nodeTime = temp2;
                    left = used - 1;
                    right = used;
                }
            }

            //常规碰撞节点
            if (used >= 2) {
                for (int i = 0; i < used - 1; i++) {
                    if (state.get(i) == -1) {
                        if (state.get(i + 1) == -1) {
                            continue;
                        } else {
                            double temp3 = (list.get(i) - list.get(i + 1)) / (2.0 * v);
                            if (temp3 < nodeTime) {
                                left = i;
                                right = i + 1;
                                nodeTime = temp3;
                            }
                        }
                    }
                }
            }

            //调度间隔节点
            if (left == -1 && right == used) {
                double dist = nodeTime * v;
                for (int i = 0; i < used; i++) {
                    double originDist = list.get(i);
                    if (state.get(i) == 1) {
                        list.set(i, originDist + dist);
                    } else {
                        list.set(i, originDist - dist);
                    }
                }
                if (used < n) {
                    list.add(used, 0.0);
                    state.put(used, 1);
                    used++;
                    currInterval = 0;
                } else if (used == n) {
                    currInterval = ta;
                }
            } else {
                //更新从碰撞节点时间前到碰撞时间节点的所有AGV的运动位置
                //如果left或right发生改变, 必须要调整相应AGV的状态, 则一定有right-left = 1.
                for (int i = 0; i < used; i++) {
                    double temp5 = list.get(i);
                    if (state.get(i) == 1) {
                        list.set(i, temp5 + v * nodeTime);
                    } else {
                        list.set(i, temp5 - v * nodeTime);
                    }
                }
                //接下来调整碰撞节点上的两个AGV的运动方向
                if (left != -1 && right != used) {
                    int temp6 = state.get(left);
                    state.put(left, -1 * temp6);
                    int temp7 = state.get(right);
                    state.put(right, -1 * temp7);
                } else if (left == -1) {
                    //这种碰撞情况, 是AGV与目标点的碰撞. 也就是有AGV成功送达任务了, 所以完成的任务要加1, 正在运送的任务要-1.
                    int temp8 = state.get(right);
                    state.put(right, -1 * temp8);
                    completed++;
                } else if (right == used) {
                    //这种碰撞情况, 是AGV与原点的碰撞. 也就是有AGV成功返回了, 所以剩余可用的AGV要随之加1.
                    list.remove(used - 1);
                    state.remove(used - 1);
                    used--;
                    //当然, 之前因为车不够而不能派发任务给AGV的情况也可以解决了, 直接结束while循环.
                }
                if (currInterval + nodeTime <= ta) {
                    currInterval += nodeTime;
                } else {
                    currInterval = ta;
                }
            }
            t += nodeTime;
        }

        //当所有任务完成, 让所有agv朝原点方向返回, 所以这一段的系统时间由最前面的车决定.
        t += list.get(0) / v;
    }

    public static void OneDestination1() {
        Scanner sc = new Scanner(System.in);
        System.out.println("请AGV的数量:");
        n = sc.nextInt();
        System.out.println("请输入每次派发AGV的间隔时间:");
        ta = sc.nextDouble();
        currInterval = ta;
        System.out.println("请输入AGV的运动速度:");
        v = sc.nextDouble();
        System.out.println("请输入区域A的任务数量:");
        TaskA = sc.nextInt();
        System.out.println("请输入原点至A的距离:");
        d1 = sc.nextDouble();
    }
}

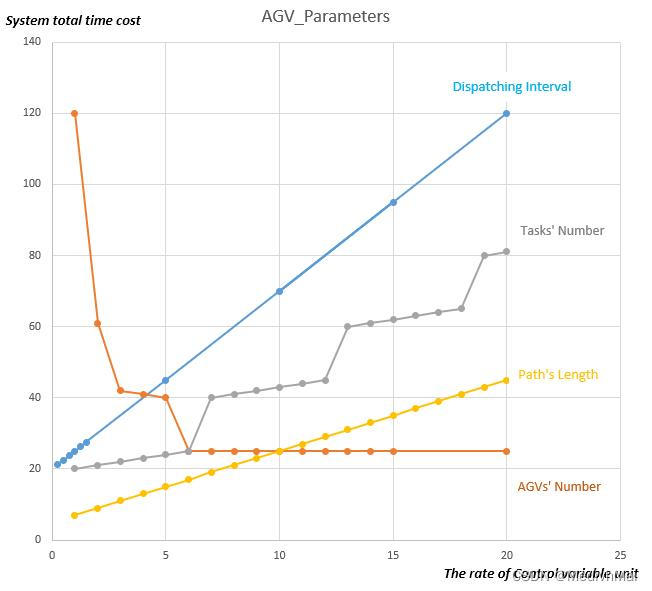
下面给出1-Path Ideal Handover Mode的单一变量比较图。

可以看出, 当其他参数不变时, 调度间隔和路径长度与系统运行时间成正比。

AGV的数量不断增加时, 系统时间会达到一个临界值。

有意思的是任务的数量与时间呈阶段性正比。其实不难理解, 因为AGV的发送与返回都是连续的。

N-Path Ideal Handover Mode

现在我们研究任意条路径的理想Handover模式。

因为需要考虑已完成路径的AGV返回情况以为新的AGV进行调度. 我们需要新增一个事件节点——返回事件节点

所以, N-Path下的四种事件节点为:

1. 常规碰撞节点

同1-Path.

2. 边界碰撞节点

同1-Path.

3. 调度间隔节点

同1-Path.

4. 返回事件节点

返回事件指除当前路径以外已派发完所有任务的路径的所有AGV的返回情况。

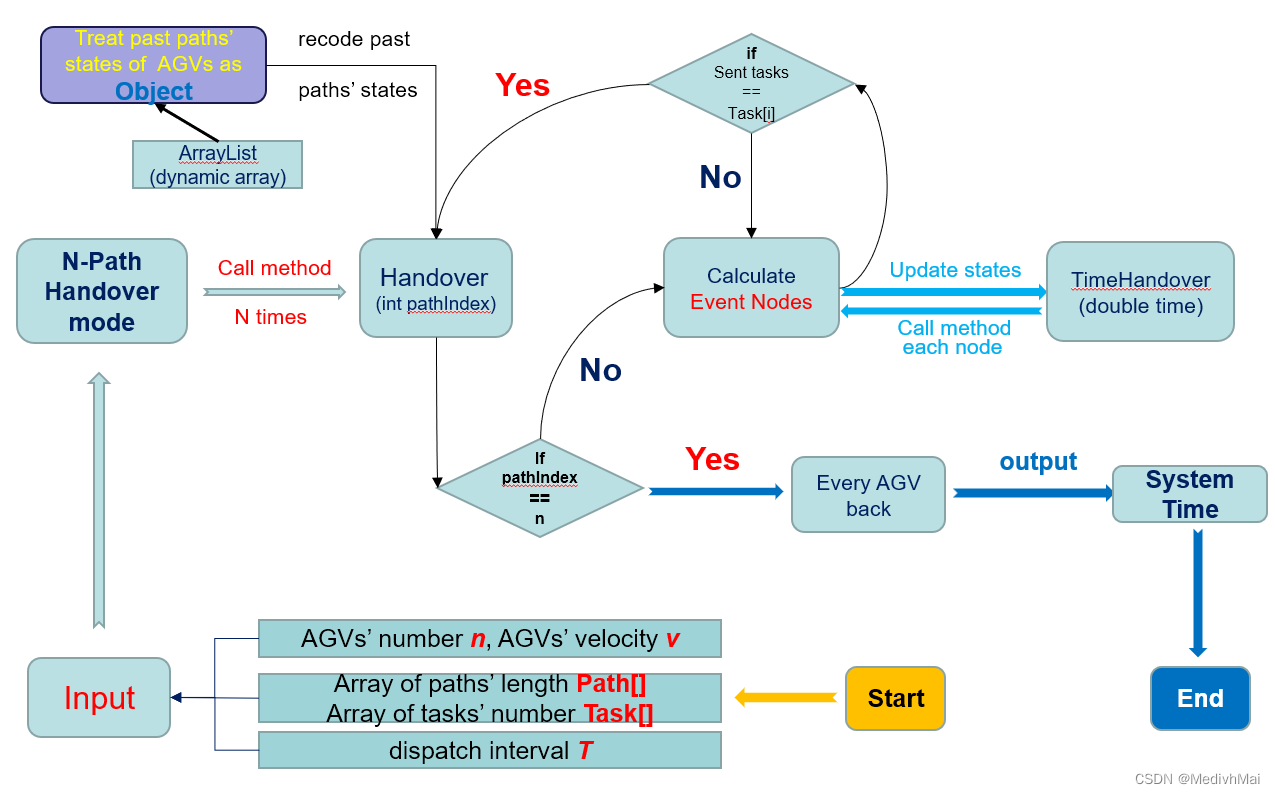
因为细节过多, 代码过于麻烦。只提供大体思路。

其他细节详见下面思维导图。

需要注意的是。还需要一个参数为时间的TimeHandover(double time)的方法更新过去路径的AGV信息, 此方法与1-Path算法的代码相似, 区别为在一个特定时间段内。

其实思路有可以优化的地方，欢迎大家一起讨论。

代码

已实现, 大概500+行。日后会给大家分享。

至此, 理想Handover模式的所有情况已全部实现。

下面开始探讨有交接时间的非理想的、普遍的Handover模式。

有交接时间的非理想Handover模式

当考虑交接时间时, 问题的性质与思路发生质变。

是否长路径依然有高优先级？是否该给一条长路径不断的派发任务(导致拥挤频繁交接)？当路径过于拥挤时, 我们要不要停止任务的派发？.......

我们先不思考这些问题, 我们首先给出单一路径下有交接时间的Handover模式(1-Path Handover Mode)。

1-Path Handover Mode

依然使用节点式计算法进行模拟, 但此时事件节点的种类与理想情况截然不同。

三种事件节点：

碰撞节点类型:

交接碰撞节点-前端碰撞
交接碰撞节点-后端碰撞
常规碰撞节点(变化)
边界碰撞节点

交接节点类型:

任务交接节点-交接开始
任务交接节点-交接结束

调度节点类型:

调度间隔节点

代码

已实现, 日后分享。

N-Path Handover Mode

接下来, 为了实现多路径的情况, 我们开始探讨开始提出的问题。

下次更新。