一、问题描述

题目描述

攀登者喜欢寻找各种地图，并且尝试攀登到最高的山峰。

地图表示为一维数组，数组的索引代表水平位置，数组的元素代表相对海拔高度。其中数组元素0代表地面。

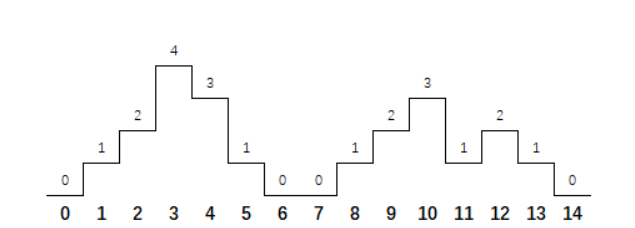
例如：[0,1,2,4,3,1,0,0,1,2,3,1,2,1,0]，代表如下图所示的地图，地图中有两个山脉位置分别为 1,2,3,4,5 和 8,9,10,11,12,13，最高峰高度分别为 4,3。最高峰位置分别为3,10。

一个山脉可能有多座山峰（高度大于相邻位置的高度，或在地图边界且高度大于相邻的高度）。

登山者想要知道一张地图中有多少座山峰。

输入描述

输入为一个整型数组，数组长度大于1。

输出描述

输出地图中山峰的数量。

用例

输入

0,1,4,3,1,0,0,1,2,3,1,2,1,0

输出

3

说明
山峰所在索引分别为3，10，12

题目解析

本题考试时为核心代码模式，非ACM模式，即无需自己解析输入数据。

本题代码实现仍然以ACM模式处理，但是会将输入处理与算法逻辑分开，大家只看算法逻辑即可。

问题分析

要解决这个问题，我们需要遍历数组，找到所有符合条件的山峰。一个位置被认为是山峰，如果它满足以下条件之一：

1. 该位置在数组的边界，并且其高度大于相邻位置的高度。
2. 该位置不在数组的边界，并且其高度大于两侧相邻位置的高度。

算法逻辑

1. 初始化计数器：设置一个计数器 peak_count 用于记录山峰的数量，初始值为0。
2. 遍历数组：从数组的第一个元素开始遍历到倒数第二个元素（因为最后一个元素单独处理）。
   • 对于每个元素，检查它是否大于其左侧和右侧的元素。如果是，则这是一个山峰，增加 peak_count。
3. 处理边界条件：
   • 检查数组的第一个元素是否大于第二个元素。如果是，第一个元素是一个山峰。
   • 检查数组的最后一个元素是否大于倒数第二个元素。如果是，最后一个元素是一个山峰。
4. 输出结果：遍历完成后，输出 peak_count 作为结果。

通过这种方法，我们可以有效地找到数组中所有的山峰，并计算它们的数量。这种方法的时间复杂度是 O(n)，其中 n 是数组的长度，因为我们只需要遍历数组一次。

二、JavaScript算法源码

以下是 JavaScript 代码的详细中文注释和讲解：

JavaScript 代码

// 引入 readline 模块，用于从标准输入读取数据
const rl = require("readline").createInterface({ input: process.stdin });

// 获取异步迭代器，用于逐行读取输入
var iter = rl[Symbol.asyncIterator]();

// 定义异步函数 readline，用于读取一行输入
const readline = async () => (await iter.next()).value;

// 输入处理
void (async function () {
  // 读取输入的一行数据，按逗号分割并转换为数字数组
  const heights = (await readline()).split(",").map(Number);

  // 调用算法函数 getResult，并输出结果
  console.log(getResult(heights));
})();

/**
 * 算法实现：统计数组中峰值的数量
 * @param {number[]} heights - 输入的高度数组
 * @returns {number} - 峰值的数量
 */
function getResult(heights) {
  let count = 0; // 初始化计数器，用于统计峰值的数量

  // 遍历数组中的每个元素
  for (let i = 0; i < heights.length; i++) {
    // 获取当前元素的左侧高度，如果左侧没有元素则默认为 0
    const leftHeight = i - 1 >= 0 ? heights[i - 1] : 0;

    // 获取当前元素的右侧高度，如果右侧没有元素则默认为 0
    const rightHeight = i + 1 < heights.length ? heights[i + 1] : 0;

    // 判断当前元素是否为峰值
    if (heights[i] > leftHeight && heights[i] > rightHeight) {
      count++; // 如果是峰值，计数器加 1
    }
  }

  // 返回峰值的数量
  return count;
}

代码讲解：

1. 输入处理：

• readline 模块：
  • 用于从标准输入逐行读取数据。
  • rl[Symbol.asyncIterator]() 获取异步迭代器，用于逐行读取输入。
• readline 函数：
  • 异步函数，用于读取一行输入。
• 输入处理逻辑：
  • 读取一行输入，按逗号 , 分割成字符串数组。
  • 使用 map(Number) 将字符串数组转换为数字数组 heights。

2. 算法实现：

• getResult 函数：
  • 参数 heights 是输入的高度数组。
  • 初始化计数器 count，用于统计峰值的数量。
  • 遍历数组中的每个元素：
    • 获取当前元素的左侧高度 leftHeight，如果左侧没有元素则默认为 0。
    • 获取当前元素的右侧高度 rightHeight，如果右侧没有元素则默认为 0。
    • 判断当前元素是否为峰值：
      • 如果当前元素大于左侧元素且大于右侧元素，则认为是峰值，计数器 count 加 1。
  • 返回峰值的数量 count。

3. 输出结果：

• 使用 console.log 输出峰值的数量。

示例运行：

输入 1：

1,2,3,2,1

• 输出：

  1
  

• 解释：
  • 数组为 [1, 2, 3, 2, 1]。
  • 只有 3 是峰值（大于左侧的 2 和右侧的 2）。
  • 峰值的数量为 1。

输入 2：

1,2,1,3,5,6,4

• 输出：

  2
  

• 解释：
  • 数组为 [1, 2, 1, 3, 5, 6, 4]。
  • 峰值有 2（大于左侧的 1 和右侧的 1）和 6（大于左侧的 5 和右侧的 4）。
  • 峰值的数量为 2。

总结：

• 该代码实现了 统计数组中峰值的数量 的功能。
• 通过遍历数组，判断每个元素是否大于其左右两侧的元素，从而确定是否为峰值。
• 时间复杂度为 O(n)，其中 n 是数组的长度。
• 如果有其他问题，欢迎继续提问！

三、Java算法源码

以下是 Java 代码的详细中文注释和讲解：

Java 代码

import java.util.Arrays; // 导入 Arrays 工具类，用于数组操作
import java.util.Scanner; // 导入 Scanner 类，用于读取输入

public class Main {
  // 输入处理
  public static void main(String[] args) {
    // 创建 Scanner 对象，用于从标准输入读取数据
    Scanner sc = new Scanner(System.in);

    // 读取一行输入，按逗号分割成字符串数组，并转换为整数数组
    int[] heights = Arrays.stream(sc.nextLine().split(","))
                          .mapToInt(Integer::parseInt)
                          .toArray();

    // 调用算法函数 getResult，并输出结果
    System.out.println(getResult(heights));
  }

  /**
   * 算法实现：统计数组中峰值的数量
   * @param heights - 输入的高度数组
   * @return 峰值的数量
   */
  public static int getResult(int[] heights) {
    int count = 0; // 初始化计数器，用于统计峰值的数量

    // 遍历数组中的每个元素
    for (int i = 0; i < heights.length; i++) {
      // 获取当前元素的左侧高度，如果左侧没有元素则默认为 0
      int leftHeight = i - 1 >= 0 ? heights[i - 1] : 0;

      // 获取当前元素的右侧高度，如果右侧没有元素则默认为 0
      int rightHeight = i + 1 < heights.length ? heights[i + 1] : 0;

      // 判断当前元素是否为峰值
      if (heights[i] > leftHeight && heights[i] > rightHeight) {
        count++; // 如果是峰值，计数器加 1
      }
    }

    // 返回峰值的数量
    return count;
  }
}

代码讲解：

1. 输入处理：

• Scanner 类：
  • 用于从标准输入读取数据。
  • sc.nextLine() 读取一行输入。
• Arrays.stream：
  • 将输入的字符串按逗号 , 分割成字符串数组。
  • 使用 mapToInt(Integer::parseInt) 将字符串数组转换为整数数组。
  • 使用 toArray() 将流转换为整数数组 heights。

2. 算法实现：

• getResult 函数：
  • 参数 heights 是输入的高度数组。
  • 初始化计数器 count，用于统计峰值的数量。
  • 遍历数组中的每个元素：
    • 获取当前元素的左侧高度 leftHeight，如果左侧没有元素则默认为 0。
    • 获取当前元素的右侧高度 rightHeight，如果右侧没有元素则默认为 0。
    • 判断当前元素是否为峰值：
      • 如果当前元素大于左侧元素且大于右侧元素，则认为是峰值，计数器 count 加 1。
  • 返回峰值的数量 count。

3. 输出结果：

• 使用 System.out.println 输出峰值的数量。

示例运行：

输入 1：

1,2,3,2,1

• 输出：

  1
  

• 解释：
  • 数组为 [1, 2, 3, 2, 1]。
  • 只有 3 是峰值（大于左侧的 2 和右侧的 2）。
  • 峰值的数量为 1。

输入 2：

1,2,1,3,5,6,4

• 输出：

  2
  

• 解释：
  • 数组为 [1, 2, 1, 3, 5, 6, 4]。
  • 峰值有 2（大于左侧的 1 和右侧的 1）和 6（大于左侧的 5 和右侧的 4）。
  • 峰值的数量为 2。

总结：

• 该代码实现了 统计数组中峰值的数量 的功能。
• 通过遍历数组，判断每个元素是否大于其左右两侧的元素，从而确定是否为峰值。
• 时间复杂度为 O(n)，其中 n 是数组的长度。
• 如果有其他问题，欢迎继续提问！

四、Python算法源码

以下是 Python 代码的详细中文注释和讲解：

Python 代码

# 输入获取
# 从标准输入读取一行数据，按逗号分割并转换为整数列表
heights = list(map(int, input().split(",")))


# 算法入口（本题实际考试为核心代码模式，因此考试时只需要写出此函数实现即可）
def getResult(h):
    count = 0  # 初始化计数器，用于统计峰值的数量

    # 遍历列表中的每个元素
    for i in range(len(h)):
        # 获取当前元素的左侧高度，如果左侧没有元素则默认为 0
        leftH = h[i - 1] if i - 1 >= 0 else 0

        # 获取当前元素的右侧高度，如果右侧没有元素则默认为 0
        rightH = h[i + 1] if i + 1 < len(h) else 0

        # 判断当前元素是否为峰值
        if h[i] > leftH and h[i] > rightH:
            count += 1  # 如果是峰值，计数器加 1

    # 返回峰值的数量
    return count


# 算法调用
print(getResult(heights))

代码讲解：

1. 输入处理：

• input() 函数：
  • 从标准输入读取一行数据。
• split(",")：
  • 将输入的字符串按逗号 , 分割成字符串列表。
• map(int, ...)：
  • 将字符串列表中的每个元素转换为整数。
• list(...)：
  • 将转换后的结果转换为整数列表 heights。

2. 算法实现：

• getResult 函数：
  • 参数 h 是输入的高度列表。
  • 初始化计数器 count，用于统计峰值的数量。
  • 遍历列表中的每个元素：
    • 获取当前元素的左侧高度 leftH，如果左侧没有元素则默认为 0。
    • 获取当前元素的右侧高度 rightH，如果右侧没有元素则默认为 0。
    • 判断当前元素是否为峰值：
      • 如果当前元素大于左侧元素且大于右侧元素，则认为是峰值，计数器 count 加 1。
  • 返回峰值的数量 count。

3. 输出结果：

• 使用 print 函数输出峰值的数量。

示例运行：

输入 1：

1,2,3,2,1

• 输出：

  1
  

• 解释：
  • 列表为 [1, 2, 3, 2, 1]。
  • 只有 3 是峰值（大于左侧的 2 和右侧的 2）。
  • 峰值的数量为 1。

输入 2：

1,2,1,3,5,6,4

• 输出：

  2
  

• 解释：
  • 列表为 [1, 2, 1, 3, 5, 6, 4]。
  • 峰值有 2（大于左侧的 1 和右侧的 1）和 6（大于左侧的 5 和右侧的 4）。
  • 峰值的数量为 2。

总结：

• 该代码实现了 统计列表中峰值的数量 的功能。
• 通过遍历列表，判断每个元素是否大于其左右两侧的元素，从而确定是否为峰值。
• 时间复杂度为 O(n)，其中 n 是列表的长度。
• 如果有其他问题，欢迎继续提问！

五、C/C++算法源码：

以下是 C 语言 代码的详细中文注释和讲解：

C 语言代码

#include <stdio.h>

#define MAX_SIZE 100000  // 定义数组的最大长度

// 算法实现（本题实际考试为核心代码模式，因此考试时只需要写出此函数实现即可）
int getResult(const int heights[], int heights_size) {
    int count = 0;  // 初始化计数器，用于统计峰值的数量

    // 遍历数组中的每个元素
    for (int i = 0; i < heights_size; i++) {
        // 获取当前元素的左侧高度，如果左侧没有元素则默认为 0
        int leftHeight = i - 1 >= 0 ? heights[i - 1] : 0;

        // 获取当前元素的右侧高度，如果右侧没有元素则默认为 0
        int rightHeight = i + 1 < heights_size ? heights[i + 1] : 0;

        // 判断当前元素是否为峰值
        if (heights[i] > leftHeight && heights[i] > rightHeight) {
            count++;  // 如果是峰值，计数器加 1
        }
    }

    // 返回峰值的数量
    return count;
}

// 输入处理
int main() {
    int heights[MAX_SIZE];  // 定义数组，用于存储输入的高度数据
    int heights_size = 0;   // 初始化数组的长度为 0

    // 循环读取输入数据，直到遇到非逗号分隔符（如换行符）
    while (scanf("%d", &heights[heights_size++])) {
        if (getchar() != ',') break;  // 如果下一个字符不是逗号，则结束输入
    }

    // 调用算法函数 getResult，并输出结果
    printf("%d\n", getResult(heights, heights_size));

    return 0;
}

代码讲解：

1. 输入处理：

• heights[MAX_SIZE]：
  • 定义一个数组 heights，用于存储输入的高度数据。
  • MAX_SIZE 是数组的最大长度，定义为 100000。
• heights_size：
  • 记录数组的实际长度，初始值为 0。
• while (scanf("%d", &heights[heights_size++]))：
  • 使用 scanf 读取整数并存储到数组 heights 中。
  • 每次读取一个整数后，数组长度 heights_size 加 1。
• if (getchar() != ',') break;：
  • 使用 getchar 读取下一个字符。
  • 如果下一个字符不是逗号 ,，则结束输入。

2. 算法实现：

• getResult 函数：
  • 参数 heights 是输入的高度数组。
  • 参数 heights_size 是数组的长度。
  • 初始化计数器 count，用于统计峰值的数量。
  • 遍历数组中的每个元素：
    • 获取当前元素的左侧高度 leftHeight，如果左侧没有元素则默认为 0。
    • 获取当前元素的右侧高度 rightHeight，如果右侧没有元素则默认为 0。
    • 判断当前元素是否为峰值：
      • 如果当前元素大于左侧元素且大于右侧元素，则认为是峰值，计数器 count 加 1。
  • 返回峰值的数量 count。

3. 输出结果：

• 使用 printf 函数输出峰值的数量。

示例运行：

输入 1：

1,2,3,2,1

• 输出：

  1
  

• 解释：
  • 数组为 [1, 2, 3, 2, 1]。
  • 只有 3 是峰值（大于左侧的 2 和右侧的 2）。
  • 峰值的数量为 1。

输入 2：

1,2,1,3,5,6,4

• 输出：

  2
  

• 解释：
  • 数组为 [1, 2, 1, 3, 5, 6, 4]。
  • 峰值有 2（大于左侧的 1 和右侧的 1）和 6（大于左侧的 5 和右侧的 4）。
  • 峰值的数量为 2。

总结：

• 该代码实现了 统计数组中峰值的数量 的功能。
• 通过遍历数组，判断每个元素是否大于其左右两侧的元素，从而确定是否为峰值。
• 时间复杂度为 O(n)，其中 n 是数组的长度。
• 如果有其他问题，欢迎继续提问！