Bootstrap

Codeforces Round 918 (Div. 4) A - F 题解

A. Odd One Out

题意：给你三个整数 a , b , c ，看看哪个数字只出现了一次。

代码：

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline int read(){
	int x = 0 , f = 1;
	char c = getchar() ;
	while(c > '9' || c < '0'){
		if(c == '-')
			f = -1 ;
		c = getchar() ;
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}
	return x * f ;
}
int t , n , k , a[maxn] ;

void solve(){
	int a , b , c ;
	a = read() ;
	b = read() ;
	c = read() ;
	map < int , int > mp ;
	mp[a] ++ ;
	mp[b] ++ ;
	mp[c] ++ ;
	if(mp[a] == 1){
		cout << a << endl ;
		return ;
	}
	if(mp[b] == 1){
		cout << b << endl ;
		return ;
	}
	cout << c << endl ;
}
int main(){
	t = read() ;
	while(t --){
		solve() ;
	}
	return 0 ;
}

B. Not Quite Latin Square

题意：给你一个3*3的方格，每行每列含有A , B , C ，要求让每一列每一行不重复。
题解：找到问号那一行，枚举哪个字母没出现即可。

代码：

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline int read(){
	int x = 0 , f = 1;
	char c = getchar() ;
	while(c > '9' || c < '0'){
		if(c == '-')
			f = -1 ;
		c = getchar() ;
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}
	return x * f ;
}
int t , n , k , a[maxn] ;
char s[10][10] ;
void solve(){
	int rt ;
	for(int i = 1 ; i <= 3 ; i ++){
		for(int j = 1 ; j <= 3 ;j  ++){
			cin >> s[i][j] ;
			if(s[i][j] == '?'){
				rt = i ;
			}
		}
	}
	map < int , int > mp ;
	for(int i = 1 ; i <= 3 ; i ++){
		if(s[rt][i] == '?'){
			continue ;
		}
		mp[s[rt][i] - 'A'] ++ ;
	}
	for(int i = 0 ; i <= 2 ; i ++){
		if(mp[i] == 0){
			cout << (char)(i + 'A') << endl ;
			return ;
		}
	}
}
int main(){
	t = read() ;
	while(t --){
		solve() ;
	}
	return 0 ;
}

C. Can I Square?

题意：给你n个数字，看看能不能正好组成一个正方形。
题解：将所有数字相加看看他们是否为完全平方数即可。

代码：

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline int read(){
	int x = 0 , f = 1;
	char c = getchar() ;
	while(c > '9' || c < '0'){
		if(c == '-')
			f = -1 ;
		c = getchar() ;
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}
	return x * f ;
}
int t , n , k , a[maxn] ;

void solve(){
	n = read() ;
	ll sum = 0 ;
	for(int i = 1 ; i <= n ; i ++){
		a[i] = read() ;
		sum += a[i] ;
	}
	if((ll)(sqrt(sum)) * (ll)(sqrt(sum)) == sum){
		cout << "YES\n" ;
	}
	else{
		cout << "NO\n" ;
	}
}
int main(){
	t = read() ;
	while(t --){
		solve() ;
	}
	return 0 ;
}

D. Unnatural Language Processing

题意：给你一个字符串，一共含有a , b , c , d , e这五个字符，a 和 e 叫做元音 ，也就是V 。 b , c , d 叫做辅音也就是C。有两种类型的音节 VC 和 VCV 。问题是他想要让你给给定的字符串划分音节，将一个音节后面的字符加上一个 . 。
题解：模拟即可，如果是 VCVC类型的就一次划分两个，如果是VCVV的一次性就划分3个，判断边界即可。复杂度 O（N）;
提醒：不要随便开STL ， 要不然会TLE 。

代码：

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline int read(){
	int x = 0 , f = 1;
	char c = getchar() ;
	while(c > '9' || c < '0'){
		if(c == '-')
			f = -1 ;
		c = getchar() ;
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}
	return x * f ;
}
int t , n , k , a[maxn] ;
char s[maxn] ;
bool vis[maxn] ;
void solve(){
	n = read() ;
	for(int i= 1 ; i <= n ; i ++){
		vis[i] = 0 ;
	}
	scanf("%s" , s + 1) ;
	map < int , int > mp ;
	mp['a' - 'a'] = 1 ;
	mp['e' - 'a'] = 1 ;
	mp['b' - 'a'] = 2 ;
	mp['c' - 'a'] = 2 ;
	mp['d' - 'a'] = 2 ;
	if(n <= 3){
		for(int i =1 ; i <= n ; i ++){
			cout << s[i] ;
		} 
		cout << endl ;
		return ;
	}
	for(int i = 1 ; i <= n ; ){
		if(mp[s[i] - 'a'] == 2){
			if(i + 1 == n){
//				vis[i + 1] = 1 ;
				i = n + 1 ;
				continue ;
			}
			if(i + 2 == n){
//				vis[i + 2] = 1 ;
				i = n + 1 ;
				continue ;
			}
			if(mp[s[i + 2] - 'a'] == 2 && mp[s[i + 3] - 'a'] == 2 && i + 2 <= n && i + 3 <= n){
				vis[i + 2] = 1 ;
				i = i + 3 ;
				continue ;
			}
			vis[i + 1] = 1 ;
			i = i + 2 ;
		}
	}
	for(int i = 1 ; i <= n ; i ++){
		cout << s[i] ;
		if(vis[i] == 1){
			cout << "." ;
		}
	}
	cout << endl ;
}
int main(){
	t = read() ;
	while(t --){
		solve() ;
	}
	return 0 ;
}

E. Romantic Glasses

题意：看能否有一个区间 l , r ，其中的奇数和等于偶数和 。
题解 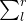：\sum_l^r（a[i] % 2 == 1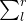）==  \sum_l^r（a[i] % 2 == 0）其实可以将奇数的所有数组转化成 -a[i] , 这样这个式子就变成了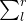\sum_l^r（a[i] % 2 == 0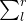） + \sum_l^r -(a[i] % 2 == 1） == 0 。所以也就是sum(r）- sum(l) == 0 ，即sum(l) == sum(r) 。 用map或set等STL维护即可。

代码：

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline ll read(){
	ll x = 0 , f = 1;
	char c = getchar() ;
	while(c > '9' || c < '0'){
		if(c == '-')
			f = -1 ;
		c = getchar() ;
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}
	return x * f ;
}
ll t , n , k , b[maxn] , lisan[maxn] ;
ll a[maxn] , sum[2][maxn] ;
void solve(){
	n = read() ;
	for(int i = 1 ; i <= n ; i ++){
		a[i] = read() ;
	}
	bool flag = 0 ;
	for(int i = 2 ; i <= n ; i ++){
		if(a[i] == a[i - 1]){
			flag = 1 ;
		}
	}
	if(flag == 1){
		cout << "YES\n" ;
		return ;
	}
	map < ll , ll > mp ;
	for(int i = 1 ; i <= n ; i ++){
		if(i % 2 == 1){
			a[i] = -a[i] ;
		}
	}
	ll sum = 0 ;
	mp[0] = 1 ;
	for(int i = 1 ; i <= n ; i ++){
		sum += a[i] ;
		if(mp[sum] == 1){
			cout << "YES\n" ;
			return ;
		}
		mp[sum] = 1 ;
	}
	cout << "NO\n" ;
}
int main(){
	t = read() ;
	while(t --){
		solve() ;
	}
	return 0 ;
}

F. Greetings

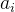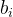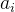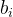题意：给你n组数，每一组数字a_i < b_i ，并且这2n个数字没有重复。每一组数都是由a_i跑到b_i的，并且每一组的速度都为1。问这些组数据相遇的次数是多少。
题解：其实可以直接看出这是道二位偏序问题，很容易想到按照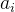a_i从小到大排序，然后再从n开始插入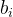b_i到树状数组中，然后依次统计贡献就是这个题的答案。但是看数据范围 1 <= 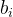b_i <= 1e9 ， 如果直接插入树状数组没有办法开那么大，但是看到n的范围是1 <= n <= 2e5 ， 所以想到离散化。将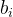b_i离散化然后倒序插入树状数组统计答案即可。整体复杂度O(nlogn) 。
注意：多测记清空！  

代码：

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline int read(){
	int x = 0 , f = 1;
	char c = getchar() ;
	while(c > '9' || c < '0'){
		if(c == '-')
			f = -1 ;
		c = getchar() ;
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}
	return x * f ;
}
int t , n , k , b[maxn] , lisan[maxn] ;
char s[maxn] ;
bool vis[maxn] ;
int T[maxn] ;
struct Node{
	int x , y ;
	bool friend operator < (const Node a , const Node b){
		return a.x < b.x ;
	}
}a[maxn] ;
int lowbit(int x){
	return x & (-x) ;
}
void insert(int x , int k){
	for( ; x <= n ; x += lowbit(x)){
		T[x] += k ;
	}
}
ll query(int x){
	ll ans = 0 ;
	while(x){
		ans += T[x] ;
		x -= lowbit(x) ;
	}
	return ans ;
}
void solve(){
	n = read() ;
	for(int i = 0 ; i <= n ; i ++){
		T[i] = 0 ;
	}
	for(int i = 1 ; i <= n ; i ++){
		a[i].x = read() ;
		a[i].y = read() ;
	}
	sort(a + 1 , a + n + 1) ;
	for(int i = 1 ; i <= n ; i ++){
		b[i] = a[i].y ;
		lisan[i] = b[i] ;
	}
	sort(lisan + 1 , lisan + n + 1) ;
	int nn = unique(lisan + 1 , lisan + n + 1) - lisan - 1 ;
	for(int i = 1 ; i <= n ; i ++){
		b[i] = lower_bound(lisan + 1 , lisan + nn + 1 , b[i]) - lisan ;
	}
	ll ans = 0 ;
	for(int i = n ; i >= 1 ; i --){
		ans += query(b[i]) ;
		insert(b[i] , 1) ;
	}
	cout << ans << endl ;
	
}
int main(){
	t = read() ;
	while(t --){
		solve() ;
	}
	return 0 ;
}

备注：如果喜欢作者的记得点赞收藏加关注哦~

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
docker存储卷
锁争用详解
mpegts介绍
软考系统架构师案例分析知识点
Chrome开发者工具详解
从零开始学Java（超详细韩顺平老师笔记梳理）04——程序控制结构：顺序、分支、(嵌套)循环、空心金字塔
qt5添加资源文件的方法
log4j+JDBC+mySQL 将对象写入数据库
一款功能强大的网络资源爬取工具
MybatisPlus快速入门
;