A. Make it White
题意:给你一串字符串,求出将所有黑色的格子变成白色的最短距离。
题解:找到左右位置,作差即可。
代码:
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline ll read(){
ll x = 0 , f = 1 ;
char c = getchar() ;
while(c > '9' || c < '0'){
if(c == '-')
f = -1 ;
c = getchar() ;
}
while(c >= '0' &&c <= '9'){
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
ll t , n , m , k , a[maxn] , b[maxn] ;
char s[maxn] ;
void solve(){
n = read() ;
scanf("%s" , s + 1) ;
int l = -1 , r = -1 ;
for(int i = 1 ; i <= n ; i ++){
if(s[i] == 'B'){
l = i ;
break ;
}
}
for(int i = n ; i >= 1 ; i --){
if(s[i] == 'B'){
r = i ;
break ;
}
}
if(r == -1 || l == -1){
cout << 0 << endl ;
return ;
}
cout << r - l + 1 << endl ;
}
int main(){
t = read() ;
while(t -- ){
solve() ;
}
return 0 ;
}
B. Following the String
题意:给你n个数字,每个数字表示字母出现的个数,找出符合要求的字符串。
题解:枚举即可,符合填入相应的字符即可。复杂度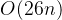 。
。
代码:
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline ll read(){
ll x = 0 , f = 1 ;
char c = getchar() ;
while(c > '9' || c < '0'){
if(c == '-')
f = -1 ;
c = getchar() ;
}
while(c >= '0' &&c <= '9'){
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
ll t , n , m , k , a[maxn] , b[maxn] ;
char s[maxn] ;
void solve(){
int cnt = 0 ;
n = read() ;
for(int i = 1 ; i <= n ; i ++){
a[i] = read() ;
}
map < int , int > mp ;
for(int i = 1 ; i <= n ; i ++){
for(int j = 0 ; j <= 25 ; j ++){
if(mp[j] == a[i]){
b[++ cnt] = j + 'a' ;
mp[j] ++ ;
break ;
}
}
}
for(int i = 1 ; i <= cnt ; i ++){
cout << (char)b[i] ;
}
cout << endl ;
}
int main(){
t = read() ;
while(t -- ){
solve() ;
}
return 0 ;
}
C. Choose the Different Ones!
题意:给你n个数字和m个数字和一个k,看能否从每串数字中提取出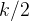 个数字,组成
个数字,组成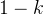 的排列。
的排列。
题解:先从a数组中计算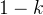 的数字个数,然后统计a中没有的数字在b中,最后看看是否有
的数字个数,然后统计a中没有的数字在b中,最后看看是否有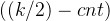 个数字在b中即可。用STL中的map维护即可。
个数字在b中即可。用STL中的map维护即可。
代码:
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline ll read(){
ll x = 0 , f = 1 ;
char c = getchar() ;
while(c > '9' || c < '0'){
if(c == '-')
f = -1 ;
c = getchar() ;
}
while(c >= '0' &&c <= '9'){
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
ll t , n , m , k , a[maxn] , b[maxn] , c[maxn] ;
char s[maxn] ;
void solve(){
ll cnt = 0 ;
n = read() ;
m = read() ;
k = read() ;
map < ll , ll > mp , p ;
for(int i = 1 ; i <= n ; i ++){
a[i] = read() ;
mp[a[i]] ++ ;
}
for(int i = 1 ; i <= m ; i ++){
b[i] = read() ;
p[b[i]] ++ ;
}
for(int i = 1 ; i <= k ; i ++){
if(mp[i] == 0){
c[++ cnt] = i ;
}
}
if(cnt > k / 2){
cout << "NO\n" ;
return ;
}
for(int i = 1 ; i <= cnt ; i ++){
// cout << c[i] << " " ;
if(p[c[i]] == 0){
cout << "NO\n" ;
return ;
}
else{
p[c[i]] = 0 ;
}
}
ll res = 0 ;
for(int i = 1 ; i <= k ; i ++){
if(p[i]){
res ++ ;
}
}
// cout << res << endl ;
if(res < ((k / 2) - cnt)){
cout << "NO\n" ;
return ;
}
cout << "YES\n" ;
}
int main(){
t = read() ;
while(t -- ){
solve() ;
}
return 0 ;
}
D. Find the Different Ones!
题意:给你n个数字,m组查询,每次查询![[l , r]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJsJTIwJTJDJTIwciU1RA%3D%3D) 中是否有
中是否有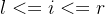 和
和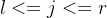 并且
并且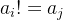 ,如果有输出不同数字的坐标,没有输出两个-1。
,如果有输出不同数字的坐标,没有输出两个-1。
题解:很明显,需要nlogn之内的复杂度来解决此问题,很容易想到二分,那么从后面向前处理最大拓展距离,查询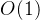 查询即可。复杂度
查询即可。复杂度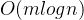 。
。
代码:
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline ll read(){
ll x = 0 , f = 1 ;
char c = getchar() ;
while(c > '9' || c < '0'){
if(c == '-')
f = -1 ;
c = getchar() ;
}
while(c >= '0' &&c <= '9'){
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
ll t , n , m , k , a[maxn] , pos[maxn] ;
char s[maxn] ;
void solve(){
n = read() ;
for(int i = 1 ; i <= n ; i ++){
a[i] = read() ;
}
pos[n] = n + 1 ;
for(int i = n - 1 ; i >= 1 ; i --){
if(a[i] == a[i + 1]){
pos[i] = pos[i + 1] ;
}
else{
pos[i] = i + 1 ;
}
}
// cout << endl ;
m = read() ;
for(int i = 1 ; i <= m ; i ++){
ll u , v ;
u = read() ;
v = read() ;
// u -- ;
// v -- ;
if(pos[u] > v)
cout << -1 << " " << -1 << endl ;
else{
cout << u << " " << pos[u] << endl ;
}
}
cout << endl ;
}
int main(){
t = read() ;
while(t -- ){
solve() ;
}
return 0 ;
}
E. Klever Permutation
题意:给你两个数字n和k,问 每个
每个 的最大值和最小值相差要小于等于1。输出合法序列。
的最大值和最小值相差要小于等于1。输出合法序列。
题解:发现一次移动1最好,这样永远不会相差超过1,那么想到一加一减,手模几组样例,很明显,先从大到小,再从小到大,不要超过范围即可。
代码:
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline ll read(){
ll x = 0 , f = 1 ;
char c = getchar() ;
while(c > '9' || c < '0'){
if(c == '-')
f = -1 ;
c = getchar() ;
}
while(c >= '0' &&c <= '9'){
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
ll t , n , m , k , a[maxn] , b[maxn] ;
char s[maxn] ;
void solve(){
n = read() ;
m = read() ;
int l = 1 , r = n ;
int rt = 1 ;
while(1){
if(l > r){
break ;
}
for(int i = rt ; i <= n ; i += m ){
a[i] = r ;
r -- ;
}
rt ++ ;
if(l > r){
break ;
}
for(int i = rt ; i <= n ; i += m){
a[i] = l ;
l ++ ;
}
rt ++ ;
}
for(int i = 1 ; i <= n ; i ++){
cout << a[i] << " " ;
}
cout << endl ;
}
int main(){
t = read() ;
while(t -- ){
solve() ;
}
return 0 ;
}
喜欢作者的记得关注点赞加收藏哦~
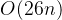 。
。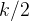 个数字,组成
个数字,组成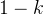 的排列。
的排列。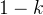 的数字个数,然后统计a中没有的数字在b中,最后看看是否有
的数字个数,然后统计a中没有的数字在b中,最后看看是否有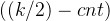 个数字在b中即可。用STL中的map维护即可。
个数字在b中即可。用STL中的map维护即可。![[l , r]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJsJTIwJTJDJTIwciU1RA%3D%3D) 中是否有
中是否有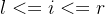 和
和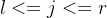 并且
并且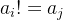 ,如果有输出不同数字的坐标,没有输出两个-1。
,如果有输出不同数字的坐标,没有输出两个-1。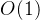 查询即可。复杂度
查询即可。复杂度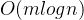 。
。 每个
每个 的最大值和最小值相差要小于等于1。输出合法序列。
的最大值和最小值相差要小于等于1。输出合法序列。