🤖 原视频： 小波变换：离散小波变换 DWT

🤖 写在前面： 本文主要基于原视频内容，同时又融合了多篇博客的内容。

前言

虽然网络上已经存在了许多介绍小波变换的博客，但是要么讲的太深，偏向于数学和物理，要么讲的太浅，一两段介绍完后就开始了代码实操部分。为了能够在周五的组会上侃侃而谈 (应付组会)，同时又不想在公式的苦海中挣扎，因此我试图通过一些浅显易懂的介绍来入门小波变换。

1 小波变换

小波变换是指，输入信号通过和小波函数做卷积，被分解为一系列的信号，对应着不同的时域信息和频域信息。因此，小波变换可以实现时频分析。

以上的表述可能不够专业，但确实很简明易懂😇

小波变换 $(\mathsf{wavelet}\mathsf{transform})$ 分为：

• 连续小波变换 $(\mathsf{continuous}\mathsf{wavelet}\mathsf{transform},\mathsf{CWT})$
• 离散小波变换 $(\mathsf{discrete}\mathsf{wavelet}\mathsf{transform},\mathsf{DWT})$

在默认的情况下，不加前缀词的 “小波变换” 指的是连续小波变换。

2 连续小波变换（CWT）

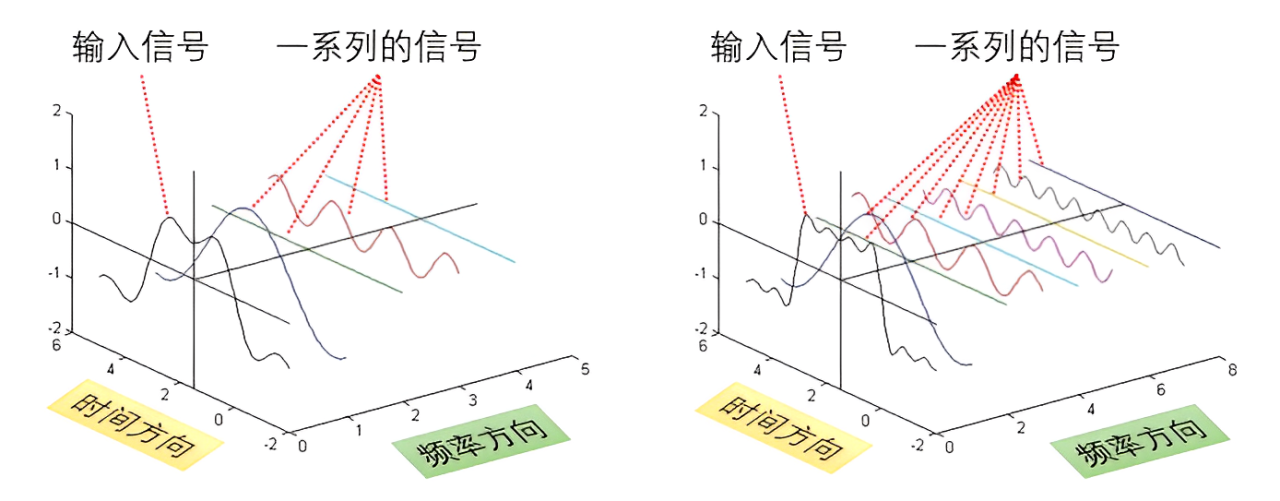
CWT 是通过一系列的小波函数来实现的。

小波函数写作 ${\varphi }_{a,b}(t)$，由母函数 $\varphi (t)$ 构建而来。具体来说，通过控制参数 $a$ 和 $b$ 对母函数进行平移和伸缩，从而得到小波函数。再让输入信号和小波函数做卷积，将输入信号分解为一系列的信号。

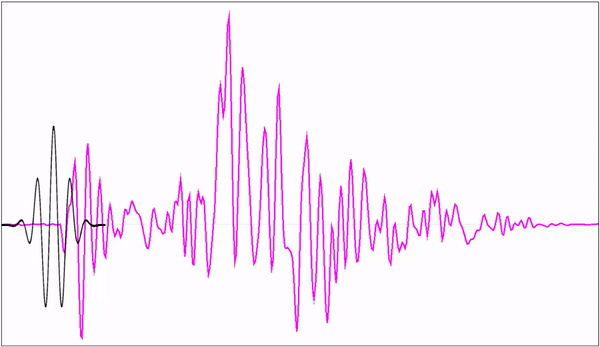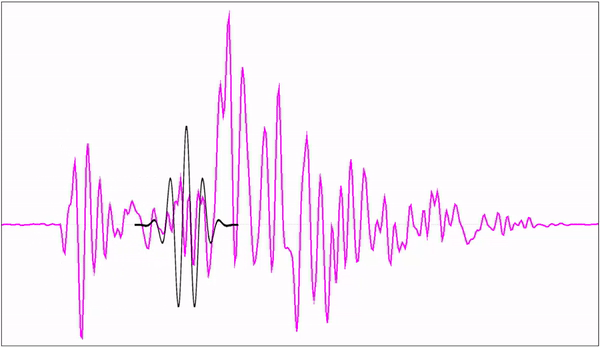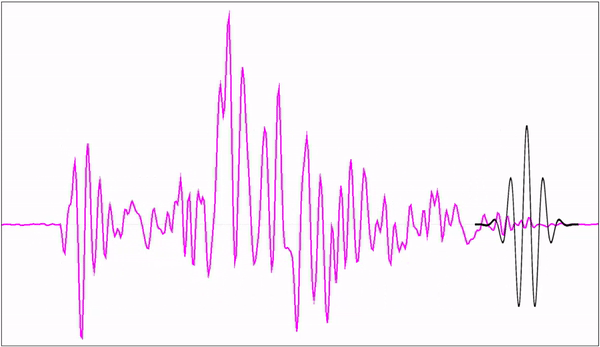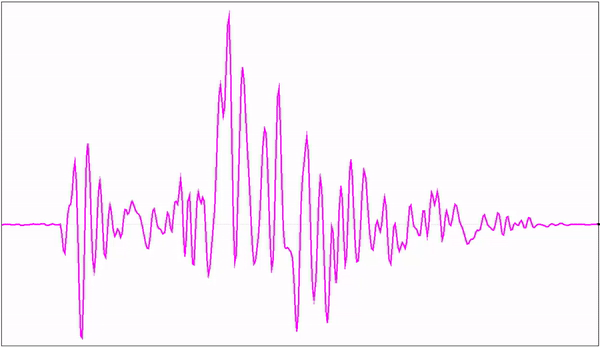
素材源自：https://blog.csdn.net/l494926429/article/details/51818012

最靠前的黑色线可以理解为一个输入信号，它后面的彩色线可以理解为一系列的信号。黑色线可以由这些彩色线叠加而成，即输入信号可以由一系列的信号叠加而成。小波变换要做的，就是将输入信号重新分解为一系列的信号。

2.1 小波函数

小波函数和母函数的关系如下：

$${\varphi }_{a,b}(t)=\frac{1}{\sqrt{a}}\varphi (\frac{t-b}{a})$$

其中，$\frac{1}{\sqrt{a}}$ 是归一化系数，$a$ 是影响频域的伸缩参数，$b$ 是影响时域的平移参数。母函数 $\varphi (t)$ 有常见的几十种函数形式可供选择。

母函数的选取也是实际应用中需要考虑的问题。

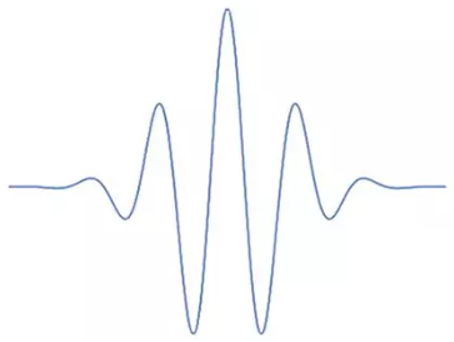
母函数的基本形状如下：

是一个振幅以 $0$ 开始，又以 $0$ 为止的短促的波。

参数 $a$ 和 $b$ 含义如下：

• 伸缩参数 $a(\mathsf{scale}\mathsf{parameter})$：$a$ 越大，周期越大，频率越小。$a$ 用于压缩或拉伸小波函数，从而可以检测信号中的不同频率成分。较小的尺度对应于压缩的小波，用于分析信号的高频部分；较大的尺度对应于拉伸的小波，用于分析信号的低频部分。
• 平移参数 $b(\mathsf{translation}\mathsf{parameter})$：$b$ 增大，函数图像左移；$b$ 减小，函数图像右移。$b$ 用于在时间轴上移动小波函数，从而可以分析信号在不同时间点的行为。

由此可见，小波变换可以同时联系频域和时域。

回顾：周期 $T=\frac{2\pi }{w}=2\pi a$，频率 $f=\frac{1}{T}=\frac{1}{2\pi a}$。原视频好像把 $a$ 和周期 $T$ 的关系说反了。

参数 $a$ 可以对小波函数进行拉伸和压缩：

如上图左侧所示，拉伸后的小波可以量化信号中的缓变信息，对应信号中低频成分；如上图右侧所示，压缩后的小波可以量化信号中的突变信息，对应信号中高频成分。

2.2 小波变换的实现

对于一个给定的原始信号 $f(t)$，其小波变换的结果为：

$$CWT(a,b)={\int }_{-\infty }^{+\infty }f(t){\varphi }_{a,b}(t)dt$$

我们通常称小波变换的结果为小波系数，将它写作 $CWT(a,b)$，意味着它是关于参数 $a$ 和 $b$ 的函数。在代码中，一般定义名为 $\mathsf{coefficients}$（即参数）的变量来存放小波系数。

连续信号 $f(t)$ 是求积分，离散信号 $f(k)$ 是求累加和。

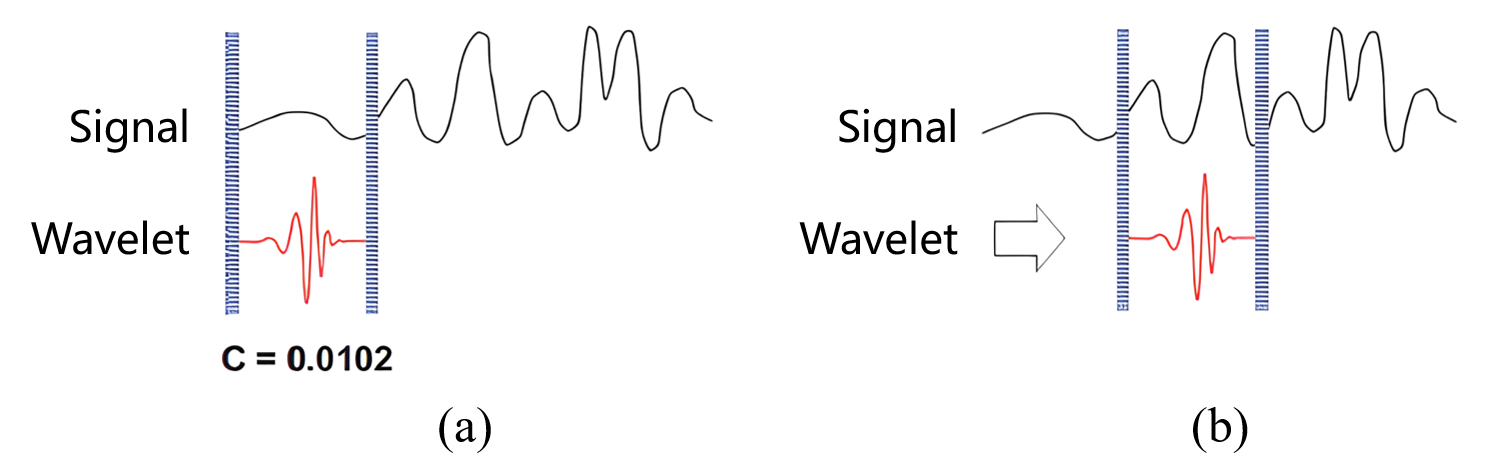
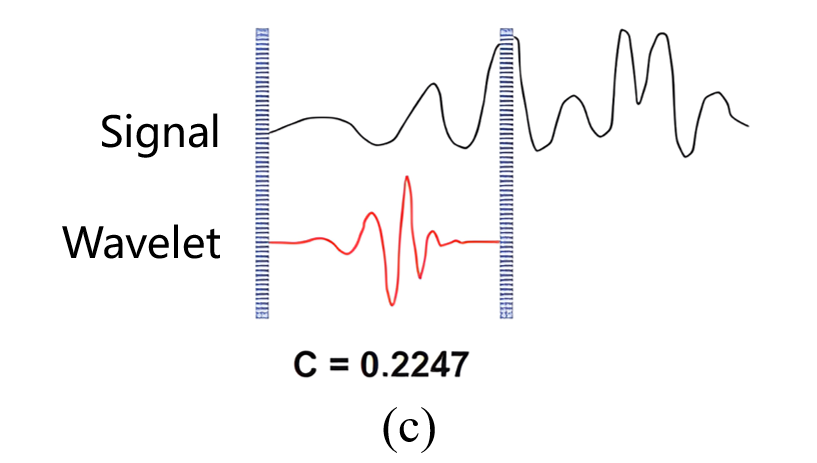
小波变换通过小波平移来提取信号中的时间信息，静态图如下图所示：

素材源自：https://blog.csdn.net/qq_18554229/article/details/134778494

1. 如图 (a) 所示，将小波函数 ${\varphi }_{a,b}(t)$ 放到原始信号 $f(t)$ 的开头处进行比较，计算小波系数 $C$。$C$ 越大，说明小波函数与原始信号这一部分的相似度越高；
2. 如图 (b) 所示，将小波函数向右平移 $b$，小波函数变为 ${\varphi }_{a,b}(t-b)$。重复前述步骤，直到小波函数位移完整个原始信号 $f(t)$；
3. 如图 (c) 所示，伸缩小波的尺度，比如：放大一倍后小波函数变为 ${\varphi }_{a,b}(2t)$，然后重复步骤 1~2 的操作；
4. 重复步骤 1~3 直到小波已经伸缩到规定的最大尺度。

动态图如下图所示：

素材源自：https://www.jishulink.com/post/433270

该动图只演示了步骤 1~2 的操作。

小波变换的具体步骤如下：

• 让不同伸缩量和平移量的小波函数与原始信号进行卷积，以确定原始信号是否具有相似的频率成分。
• 每个小波具有特定的 “频率”，卷积结果将确定各个平移量（时间）处的原始信号是否也包含相同的频率。

即通过小波变换可以确定原始信号在什么时间存在什么频率成分。

简而言之，就是把原始信号和一个选定的小波函数做卷积。这个小波函数由参数 $a$ 和 $b$ 来控制，其中参数 $a$ 可以控制小波的胖和瘦，即对应于低频和高频。如果小波正好和原始信号对得上，那么卷积值就大；如果对不上，那么卷积值就小。通过这样的方式可以知道，时域信号的频域情况。

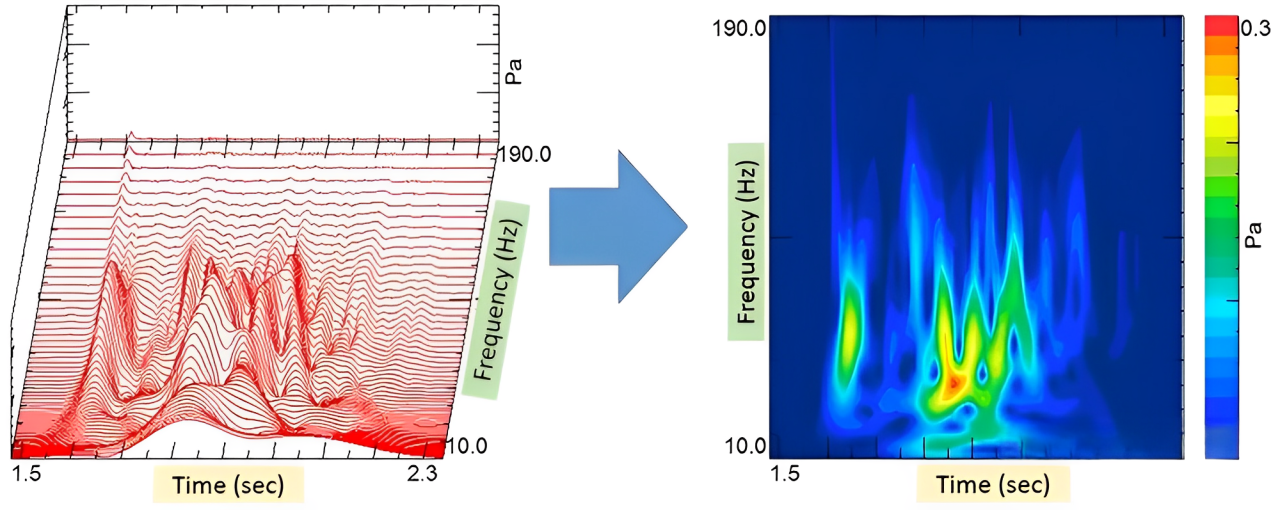
从而可以绘制出时频图：

其中，左图是一个三维图，正面是时域图，侧面是频域图。右图是一个二维图，描述的是从上往下观察左图的情况，是一个时频图。

补充：傅里叶变换只能得到频域图。

3 离散小波变换（DWT）

理论上参数 $a$ 和 $b$ 可以是整数，也可以是小数。但在 DWT 中，$a$ 和 $b$ 必须是某一个整数的倍数。常见的整数是 2，如下所示：

• $a=2^j(j=1,2,...)$
• $b=ka=k\cdot 2^j(j=1,2,...)$

其中，$j$ 是离散分解水平，$j$ 取不同的值，将设置信号被分解为 $j$ 层。比如，$j=1$ 时分解两层，$j=2$ 时分解四层。$k\in Z$ 是参数，且是一个整数。

小波函数进一步被表示为 ${\varphi }_{j,k}(n)$，表示受参数 $j$ 和 $k$ 的控制。

DWT 的结果分为两部分：

• 近似参数 $(\mathsf{approximation}\mathsf{coefficients},\mathsf{CA})$：高尺度 $(\mathsf{high}\mathsf{scale})$，低频率 $(\mathsf{low}\mathsf{frequency})$
• 细节参数 $(\mathsf{detail}\mathsf{coefficients},\mathsf{CD})$：低尺度 $(\mathsf{low}\mathsf{scale})$，高频率 $(\mathsf{high}\mathsf{frequency})$

前者提取的是低频分量，后者提取的是高频分量。

当离散分解水平取值为 $j$ 时，离散信号 $f(k)$ 的小波系数为：

• CA：$A_j={\sum }_{n=0}^{\infty }f(n){\varphi }_{j,k}(n)={\sum }_{n=0}^{\infty }f(n)\frac{1}{\sqrt{2^j}}\varphi (\frac{n-k\cdot 2^j}{2^j})$
• CD：$D_j={\sum }_{n=0}^{\infty }f(n){\varphi }_{j,k}(n)={\sum }_{n=0}^{\infty }f(n)\frac{1}{\sqrt{2^j}}\varphi (\frac{n-k\cdot 2^j}{2^j})$

即每一个时间点都要和小波函数进行运算。

plq：虽然上面两个公式长得一样，但实际上高频和低频所使用的母函数 $\varphi (t)$ 是不一样的，分别被称为高通滤波器和低通滤波器。

4 应用：降噪

我们通常认为信号中的高频分量是噪声，因此我们需要将高频分量给去除掉：

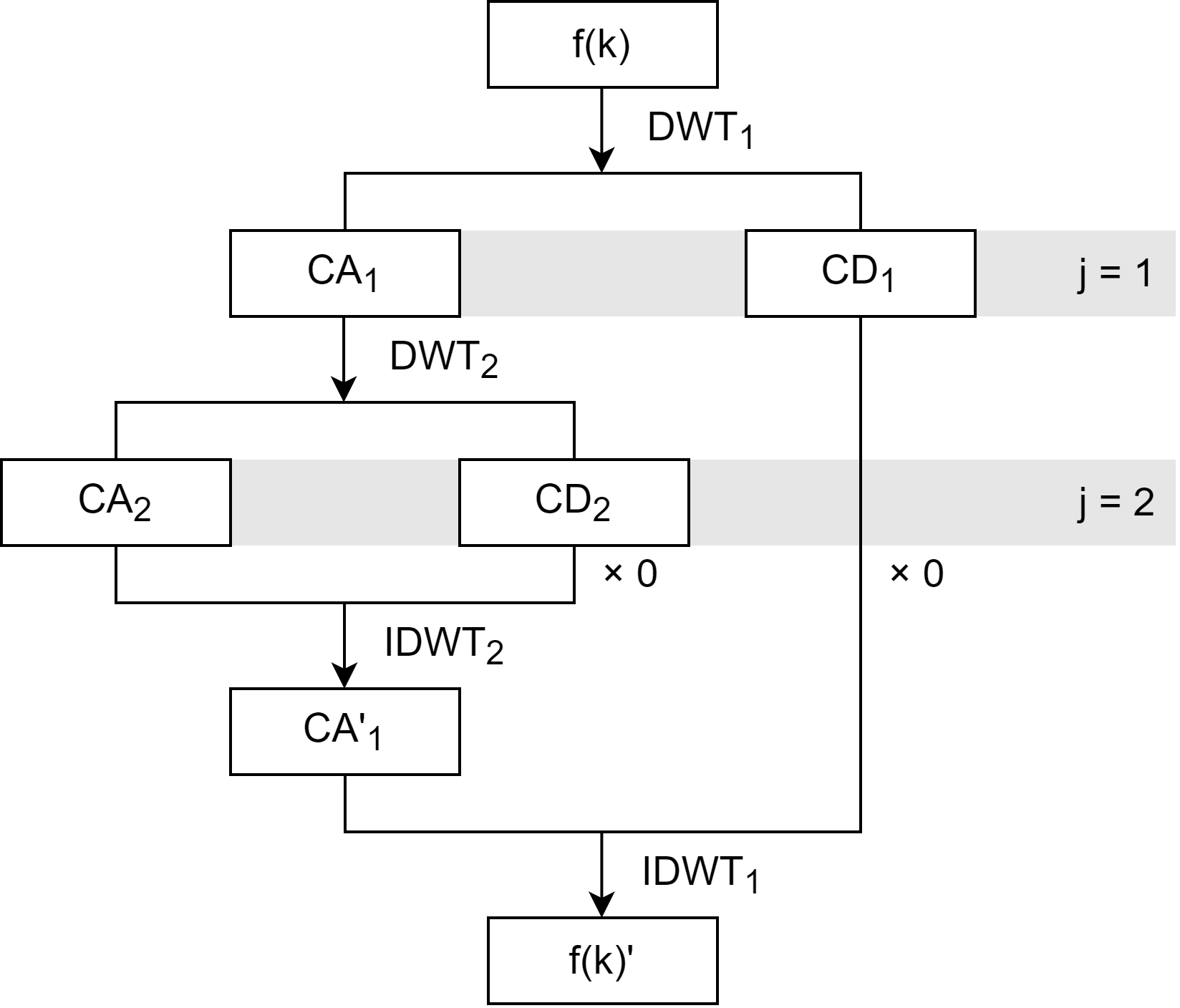
首先，对原始信号 $f(k)$ 做小波变换，得到低频分量 $C{A}_1$ 和高频分量 $C{D}_1$。由于 $C{A}_1$ 中可能仍然留存了一些高频分量，因此我们对 $C{A}_1$ 再做一次小波变换，得到低频分量 $C{A}_2$ 和高频分量 $C{D}_2$。

此时，我们认为高频分量已经去除的差不多了，因此开始做逆小波变换。我们直接将 $C{D}_2$ 乘 $0$，并和 $C{A}_2$ 一起还原得到 $C{A}_1^{\prime }$。同理，将 $C{D}_1$ 乘 $0$，并和 $C{A}_1^{\prime }$ 一起还原得到 $f(k{)}^{\prime }$，即为降噪后的信号。

说明：图中的下标都表示的是 $j$ 层数。