AE、VAE、VQVAE、VQGAN介绍

文章目录

前言
一、AE
二、VAE
三、VQVAE
四、VQGAN

前言

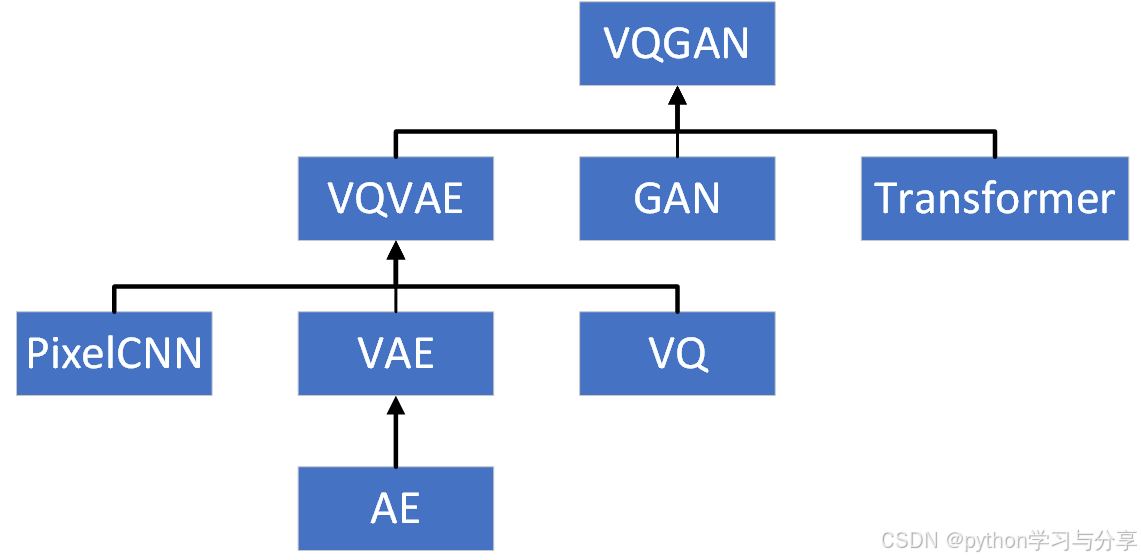
VAE、VQVAE、VQGAN是图像生成方向的模型，他们之间的关系如下图所示。接下来对这AE、VAE、VQVAE、VQGAN进行介绍。
在这里插入图片描述

一、AE

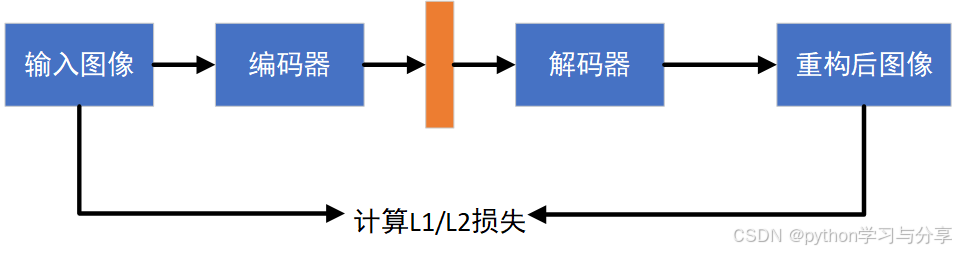
AE（AutoEncoder）中文名字叫自编码器，一种无监督学习的神经网络模型。AE的结构如下图所示：
在这里插入图片描述
对于输入的训练数据，首先使用编码器提取特征，然后使用解码器将其恢复成图像，通过计算重构后图像与原输入图像之间的L1/L2损失来实现无监督的训练。在训练完成后，可以认为编码器学习到了图像的特征提取能力，使用编码器去做图像的特征提取。
而解码器可以用作图像生成，输入是特征向量，输出是一张图片。但是AE的解码器只能将见过的特征进行重构恢复成照片，对于没有见到过的特征他是不能生成图像的。也就是AE的解码器只能将训练过程中AE编码器产生的特征重构成图片。这是AE编码器用作图像生成时的最大缺点。

二、VAE

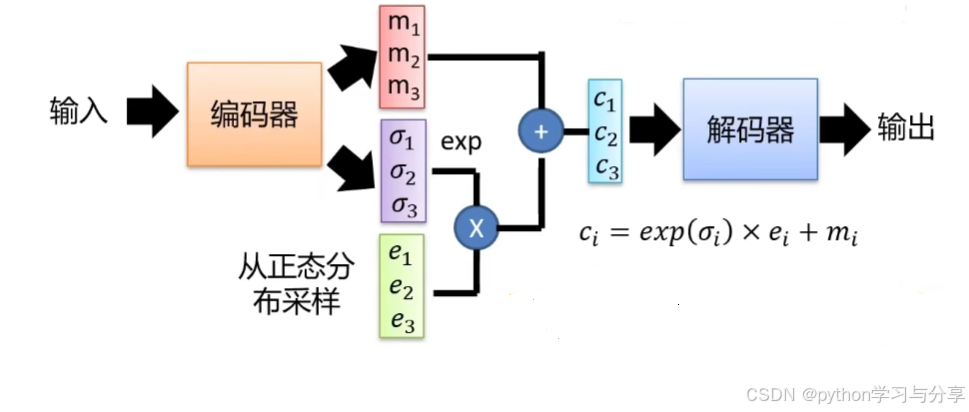
VAE（Variational AutoEncoding，变分自编码器）在2013年的一篇论文《Auto-Encoding Variational Bayes》中提出。前面说过AE在生成图像中最大的问题是只能生成训练过程中见过的特征。为了解决这个问题，VAE的思想是解码器产生的不在是特征向量，而是均值和方差。通过编码器产生的均值和方差进行采样然后送进解码器中产生图片。如下图所示：
在这里插入图片描述
VAE流程
具体的说，对于输入的图片通过编码器后，编码器可以通过两个全连接层分别产生两个向量 $m_1,m_2,m_3]$ (均值）和 $[\sigma_1,\sigma_2,\sigma_3]$ (方差），然后我们在正太分布中随机采样一个噪声向量 $e_1,e_2,e_3]$ ，然后通过公式 $exp(\sigma)*e+m=c$ 得到 $c$ 然后送给解码器进行解码。也就是说模型编码器产生的 $\sigma$ 控制噪声的大小，之所以进行exp操作是因为编码器输出的 $\sigma$ 有可能是负的，通过exp操作将其全部变成正数。
损失函数
VAE的损失函数有两部分组成，一部分是重构Loss，和AE中的损失函数相同；另一部分是一个约束条件，公式如下：

\sum_{i=1}^3(\exp(\sigma_i)-(1+\sigma_i)+(m_i)^2)

前面我们说过， $\sigma$ 是由模型学习产生的，那么在训练过程中模型会寻求捷径将 $\sigma$ 全部变成0，这样就变成了AE模型。因此，为了防止 $\sigma$ 变成0，需要将其进行约束，具体的推导过程这里就不详细介绍了。 $m_i)^2$ 是正则项。
因此VAE通过最小化重构Loss和上述约束条件进行模型训练。
推理
在VAE训练完成后，只需要在正态分布中随机采样一组噪声向量 $e_1,e_2,e_3]$ 送给解码器便可以产生图片。
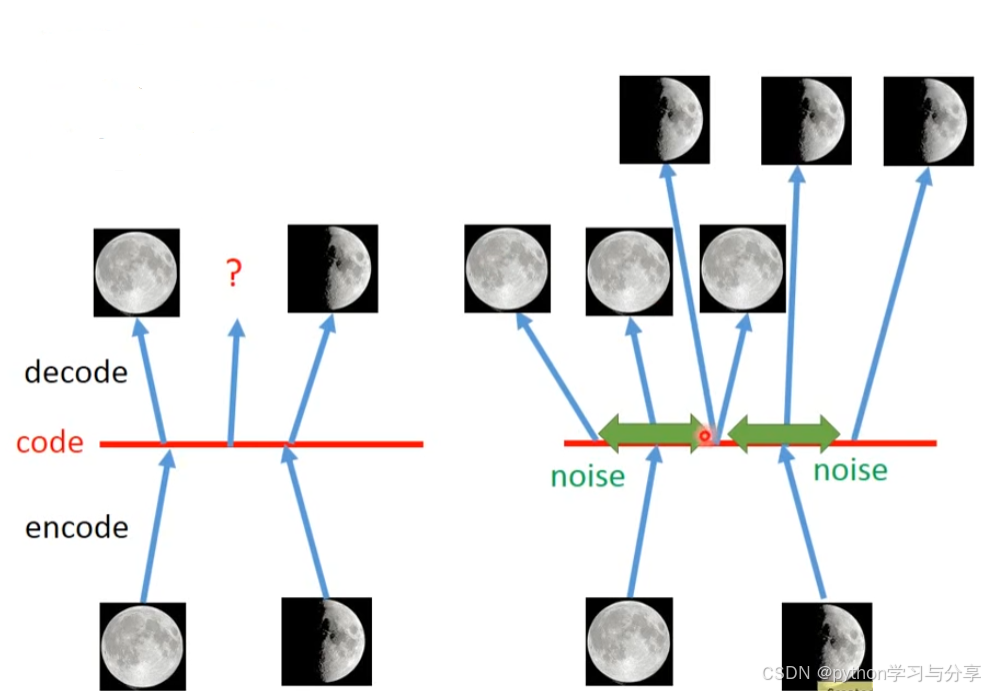
AE和VAE的直观理解如下图所示：
在这里插入图片描述
AE只能将在训练过程中遇见过的code恢复成照片，对于训练过程中没有遇到过的code不能将其恢复成图片，导致其生成的图片没有多样性。而VAE通过在编码器的输出中增加噪声解决这一问题，例如将code中生成满月和半月的点变成了一个范围区间，那么这两个范围区间的交点要生成既是满月又是半月的图片，那么综合下来就是3/4满月，这样增加了生成数据的多样性。

三、VQVAE

VQVAE在2018年的一篇论文《Neural Discrete Representation Learning》中被提出。在VAE中，隐藏空间是连续的，VAE通过在一个分布中进行采样送进解码器中进行图片生成。而VQVAE的作者认为离散的形式更加符合自然界的规律，例如在NLP中一句话首先变成一个个离散的输入到模型中。因此VQVAE引入了向量离散化（VQ,Vector Quantisation）的思想，将隐空间变成离散的。为了学习到离散的隐藏空间表示，VQVAE引入了一个码本，这个码本可以看成Transformer中的embedding层，也是可学习的。通过使用VQ的思想避免了VAE中的后验坍塌现象。
后验坍塌：在VAE的损失函数中，由于正则项的存在，导致编码器不如解码器能力强大，也就是模型过分依赖于解码器的重构能力而忽略了编码器的特征提取能力（后验分布 $q (z ∣ x)$ ， $z$ 为编码器输出的隐空间， $s$ 为编码器输入的图像）。

VQVAE与VAE不同的两点在于：1.编码器的输出是离散的，而不是连续的code。2.先验信息是可学习的而不是静态的。(这里的先验信息指的是在隐空间中进行采样然后送进解码器中的信息分布。)

模型结构
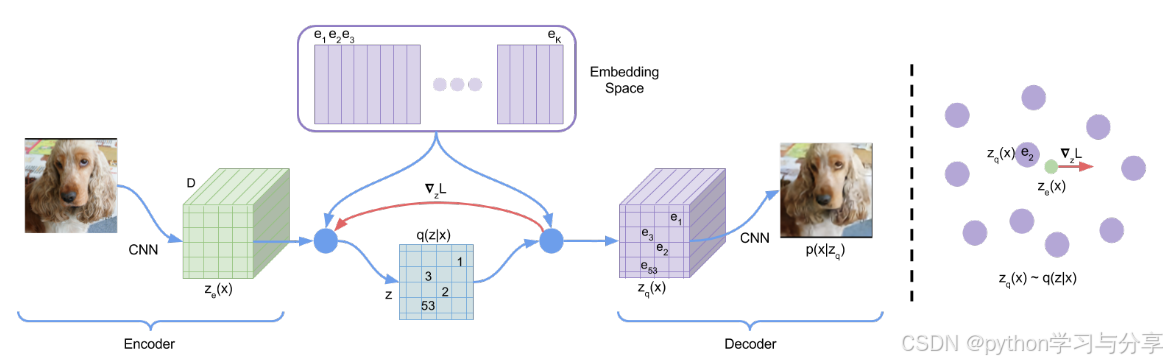
在这里插入图片描述
VQVAE的所有参数由编码器、码本、解码器三部分组成。
其整体流程如下：对于输入的图片，首先使用编码器进行特征提取得到压缩后的特征图 $z_e(x)$ (对于图片来说，特征图也是三维的（H,W,C）,相当于把一张大图压缩成一张小图)。
然后将编码器的输出特征在通道维度上与码本中的向量做最近邻查找，将 $z_e(x)$ 替换成码本中与其最相近的 $z_q(x)$ 。由 $z_e(x)$ 得到 $z_q(x)$ 公式为：

z_q(x)=e_k, where \space k =\argmin_j||z_e(x)-e_j||_2

其中，e为码本，码本是一个 $K * D$ 维的embedding层， $K$ 代表是一个K分类问题， $D$ 代表隐空间编码向量的维度数。 $e_k$ 为码本中第k个向量。码本中的每个向量都可以代表生成图像的不同特征，通过离散化使得这些特征解耦。
最后将得到的 $z_q(x)$ （同样是三维，（H,W,C））送给解码器得到图片。

损失函数
由 $z_e(x)$ 得到 $z_q(x)$ 的过程可以看作是查找替换，在进行梯度回传的时候， $z_q(x)$ 到 $z_e(x)$ 是没有梯度的，因此，梯度不能传到编码器和码本中。然后， $z_q(x)$ 的梯度和 $z_e(x)$ 的梯度可以近似看作是一样的，因此只需要将z_q(x)处的梯度直接复制给 $z_e(x)$ 即可。如上图中红色线部分所示。
最终，VQVAE的损失函数由三部分组成，其公式如下：

\log p(x|z_q(x))+||sg[z_e(x)]-e||_2^2+\beta||z_e(x)-sg[e]||_2^2

其中，sg代表停止梯度运算，第一项代表重构Loss，用来优化编码器和解码器；第二项用于优化码本，前面说过梯度直接跳过码本，所有重构Loss并不能用来优化码本，VQVAE使用最近但的字典学习算法用来优化码本；第三项用于使编码器的更新速度和码本的更新速度保持一致。

模型完整的似然可以 $\log p(x)$ 可以写作如下：

\log p(x)=\log \sum_kp(x|z_k)p(z_k)

由于解码器的似然分布 $p (x ∣ z)$ 中， $z=z_q(x)$ ，对于 $z$ 不等于 $z_q(x)$ 的k，似然分布 $p(x|z_k)$ 应该为0，所以

\log p(x)\approx \log p(x|z_q(x))p(z_q(x))

模型训练
VQVAE的训练相当于是一个二阶段的训练，先训练编码器、解码器和码本，然后在训练用于自回归产生先验的PixelCNN。
模型推理
当模型训练完成还不能直接用来推理。对于VAE来说，解码器的先验输入是通过在高斯分布中采样得到的，其输入可以有无限种可能；而对于VQVAE来说，其解码器的先验输入是在码本中得到的，采样特征选择是有限的，这样做可以使分布的方差得到约束，但不能直接通过随机采样送给解码器得到。那如何得到呢？
VQVAE是通过训练一个自回归的模型PixelCNN让其自回归的产生一个二维的特征向量，这个向量中的每一个值代表在码本中的索引，然后根据索引值获得码本中的向量，最后得到一个三维的压缩特征图。
可以把码本看作NLP中的词表，PixelCNN看作是Transformer，PixelCNN自回归产生先验分布的过程可以看作是Transformer自回归产生句子的过程。
这也就是前面说到的VQVAE和VAE不同之处，VQVAE的先验是可以学习的而不是动态的，其在生成图像的过程中，输入给解码器的先验是由可学习的自回归模型PixelCNN产生的。

四、VQGAN

VQGAN是2021年CVPR中的一篇论文，论文名字叫《Taming Transformers for High-Resolution Image Synthesis》，驯服Transformer用于高分辨率图像合成。VQGAN相当于是在VQVAE的基础上改进而来，其将模型结构换成了GAN，将编码器-解码器整体看作一个生成器；并且由于当时Transformer在NLP自回归模型取得了很大的成功，VQGAN将VQVAE中用于自回归产生先验分布的PiexlCNN换成了Transformer。（VQVAE提出的时候Transformer还没有现在这么火）VQGAN中用了Sliding attention window可以合成高分辨率的图片，并且可以用于条件生成（这时stable diffusion还没有出现）。
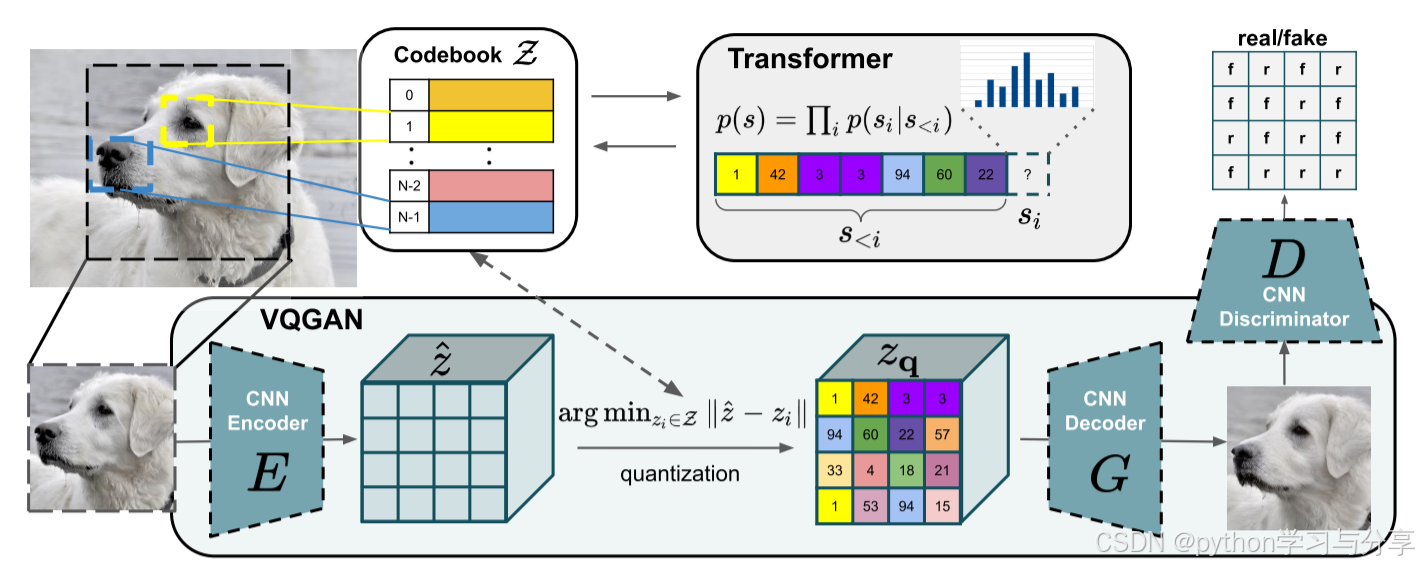
模型结构
在这里插入图片描述
VQGAN的模型结构如上图所示，模型包括编码器，解码器，码本和鉴别器。其整体流程与VQVAE相似。
模型训练
模型训练过程中也分为两阶段，首先训练整体GAN，包括编码器，解码器，码本和鉴别器，第二阶段训练Transformer进行自回归生成先验。
优化目标
在进行第一阶段的训练时，VQGAN的优化目标为：

Q^*=\argmin_{E,G,Z}\max_DE_{x-~p(x)}[L_{VQ}(E,G,Z)]+\lambda L_{GAN}(\{E,G,Z\},D)]

其中， $L_{VQ}(E,G,Z)$ 就是VQVAE中的损失，用来训练编码器，解码器和码本，其公式为:

L_{VQ}(E,G,Z)=||x-\hat{x}||^2+||sg[E(x)]-z_q||_2^2+\beta||sg[z_q]-E(x)||_2^2

$L_{GAN}$ 为对抗性损失，用来训练鉴别器，其公式为：

L_{GAN}(\{E,G,Z\},D)=[\log D(x)+\log(1-D(\hat{x}))]

参数 $\lambda$ 为自适应权重，根据重建损失和梯度来确定。
当第一阶段训练完成，进行第二阶段Transformer的训练。Transformer的特点是输入维度和输出维度相同。训练是在潜在空间完成的，也就是训练时Transformer的输入是由码本向量的索引所组成的序列，输入一串序列，去预测序列的下一个值是什么。其优化目标可以看作最大化下面的似然：

L_{Transformer}=E_{x-p(x)}[-\log p(s)]

\prod_{i}p(s_i|s_{<i})

当涉及条件生成是，优化目标为

p(s|c)=\prod_ip(s_i|s_{<i},c)

模型推理
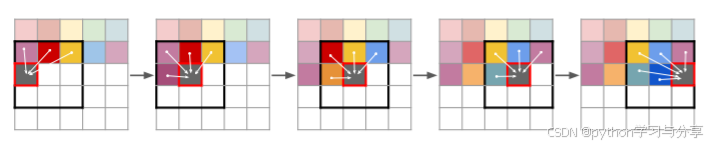
当训练完成进行推理时，与VQVAE相似，使用Transformer进行自回归生成，不过与传统的Transformer不同的是，VQGAN使用的是Sliding attention window进行自回归生成，如下图所示：
在这里插入图片描述
也就是当预测A位置的值时，Transformer输入是以A位置为中心点的九宫格里已经被预测出来的位置的值。当Transformer自回归生成结束后，得到一个二维向量，向量中的每个值就代表码本中的索引，根据索引去得到码本中的向量值（每个索引代表的向量可以看作是图片中的不同特征，将图片特征进行解耦），最后得到一个三维向量，输入到解码器中最终生成图像。