目录
2 BP神经网络:通过反投影算法进行脉冲聚光灯 SAR 模拟和重建
5 通过二维匹配滤波进行脉冲聚光灯 SAR 仿真和重建(波前重建)
7 AM - PM Stripmap SAR 信号的 CTFT
1 概述
随着计算机与网络技术的发展,目前视频监控已经发展到基于IP网络的全数字监控时代,进入第三代全数字网络视频监控时代。这个时代的代表产品以IPC、NVR为主。但是这些数字产品受恶劣天气(雾、雨、风、光等)和监控系统自身技术条件的限制,视频图像往往达不到理想效果,图像质量不稳定导致对识别、取证、事件分析等操作造成困难,使系统无法正常应用。因此,图像信号处理技术的研究和应用在安防领域具有很重要的意义。
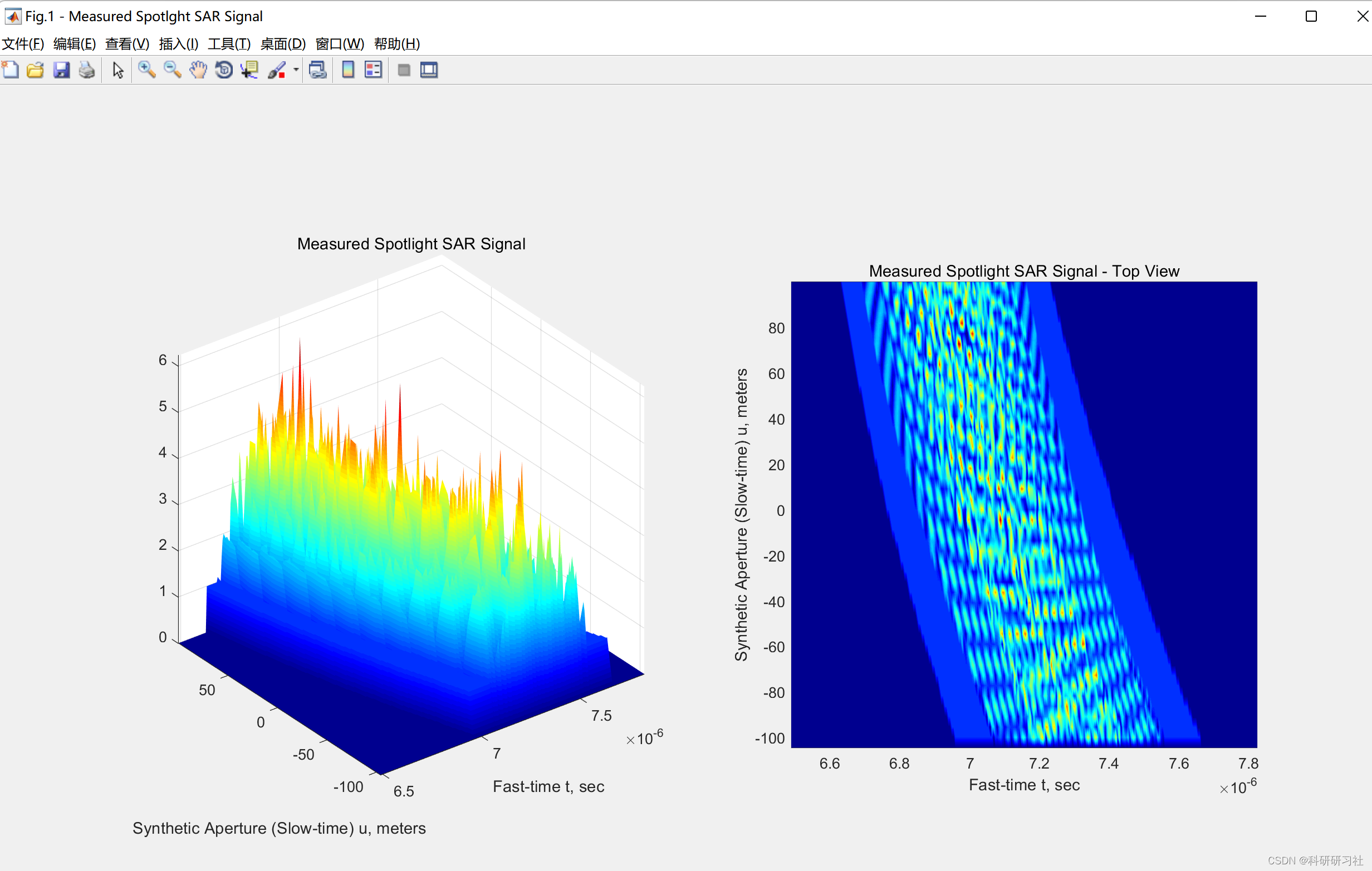
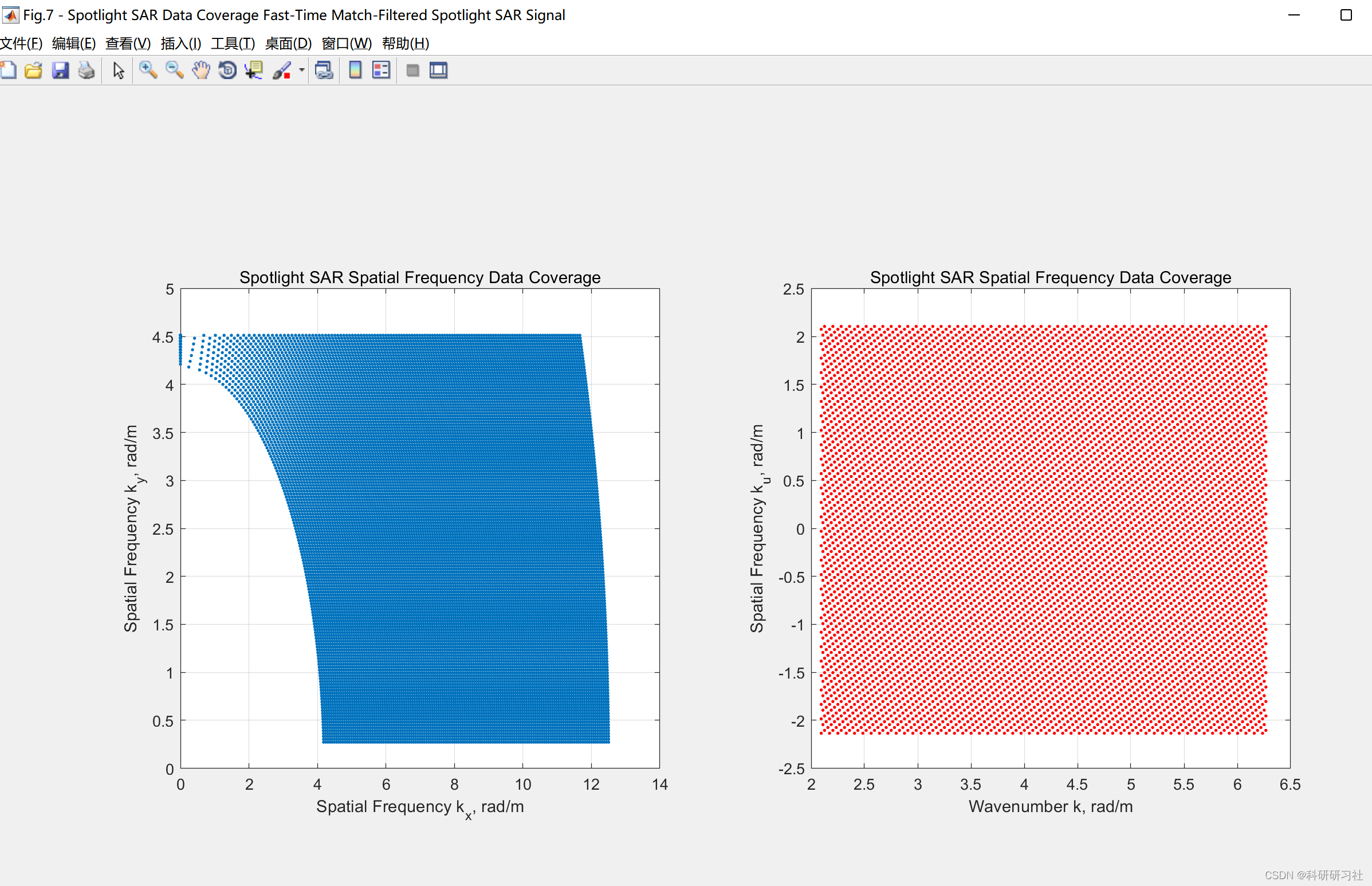
- 本文提供的4种目标风光重建算法的分离和模块化:2D匹配滤波(波前重建),时域相关(TDC),反向投影(BP)和范围堆叠(RS)。
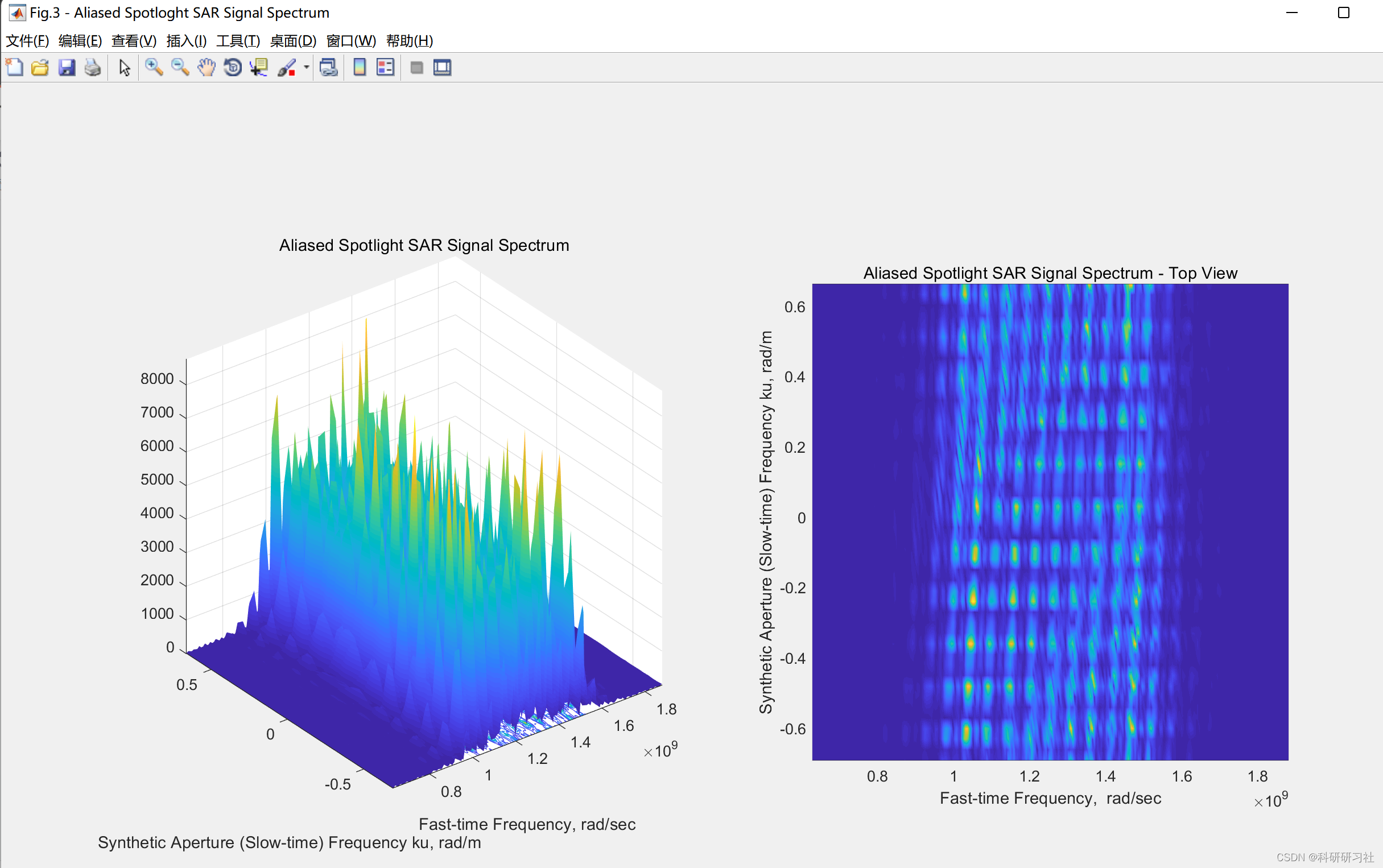
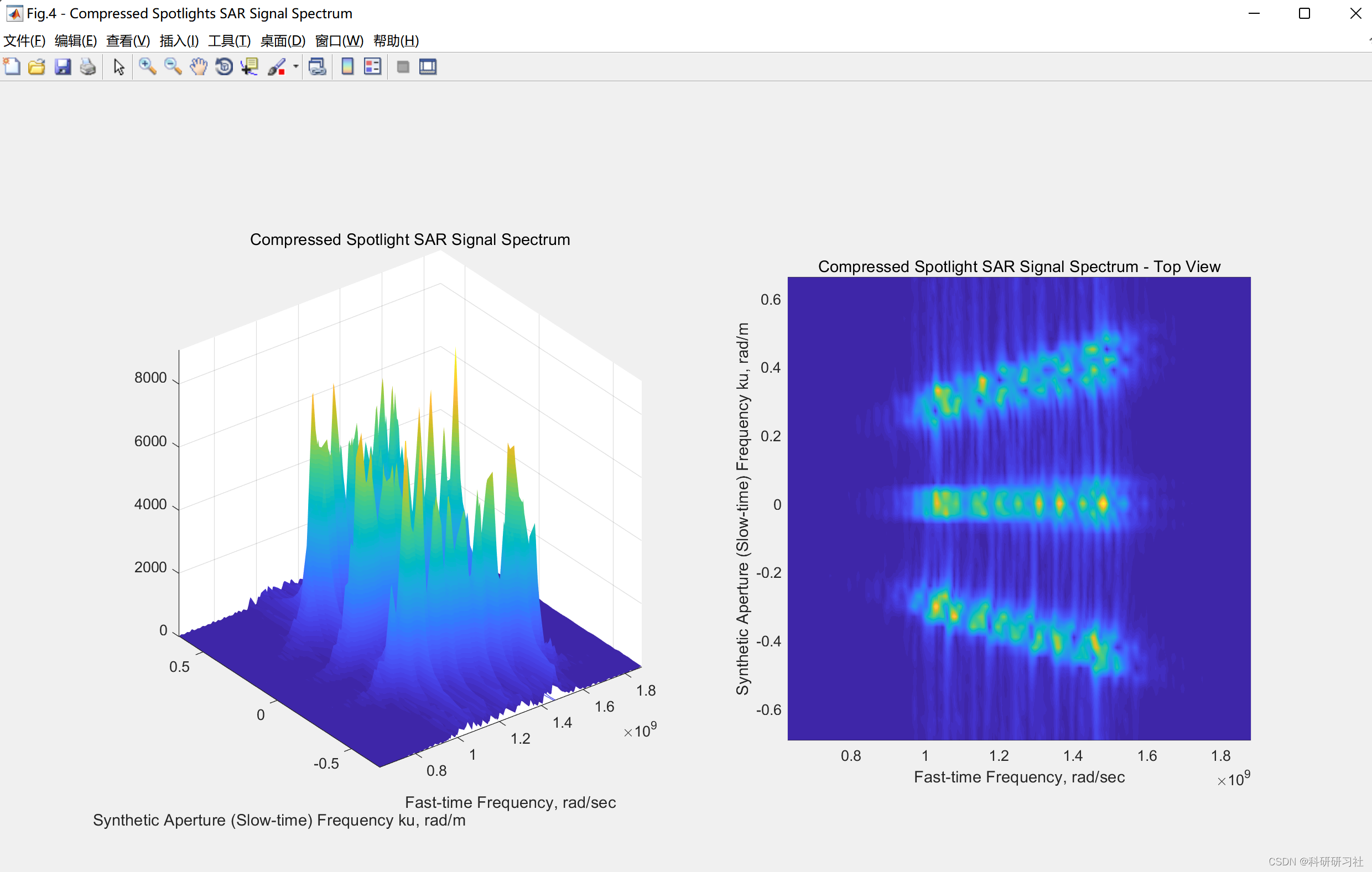
- 用现代渲染命令替换过时的图形命令,清楚地显示DSP操作对SAR信号的影响。
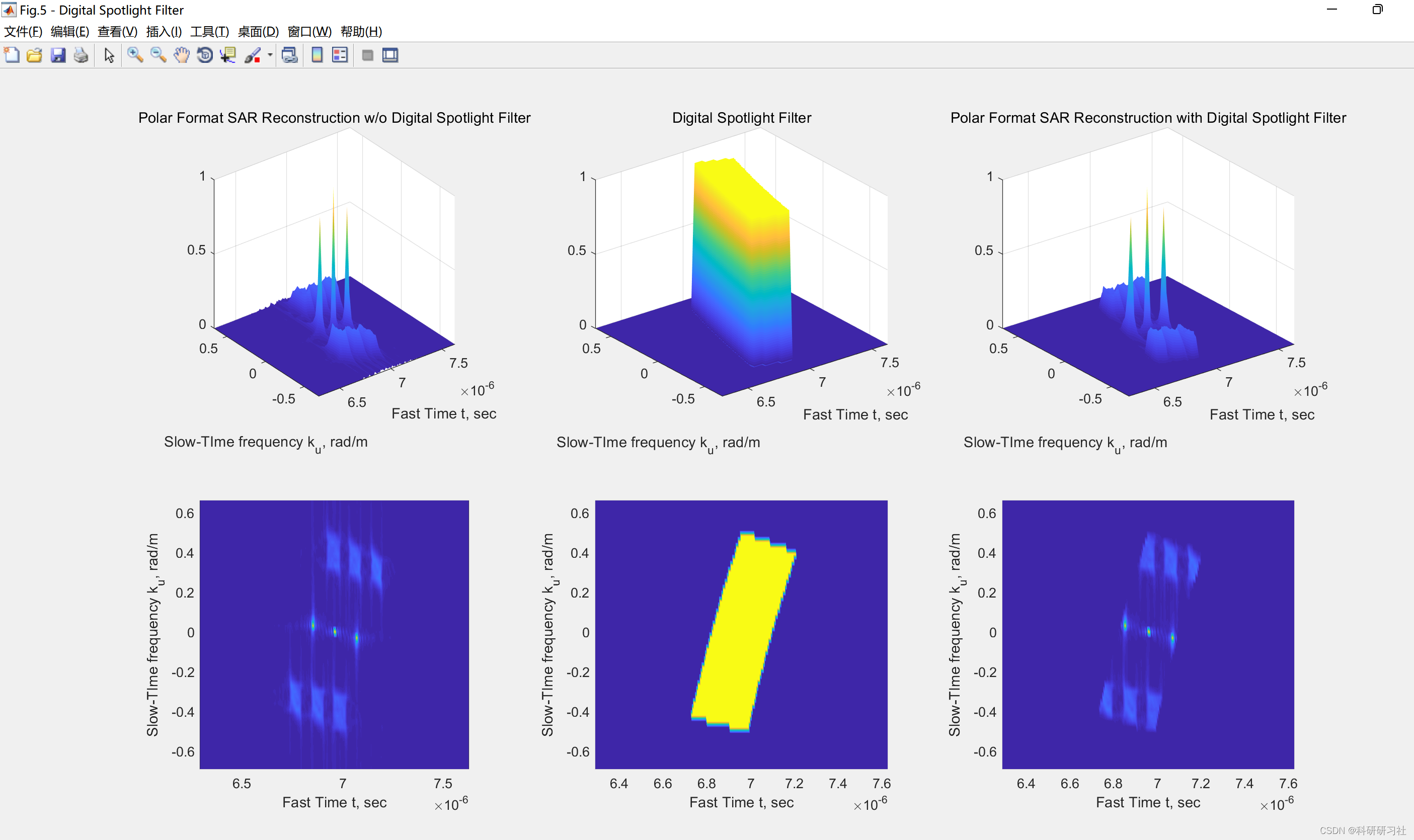
- 删除了用于对 (kx,ky) 域中间隔不均匀的数据进行二维插值的笨拙代码,并替换为不那么繁琐且更优雅的 MatLab 代码。
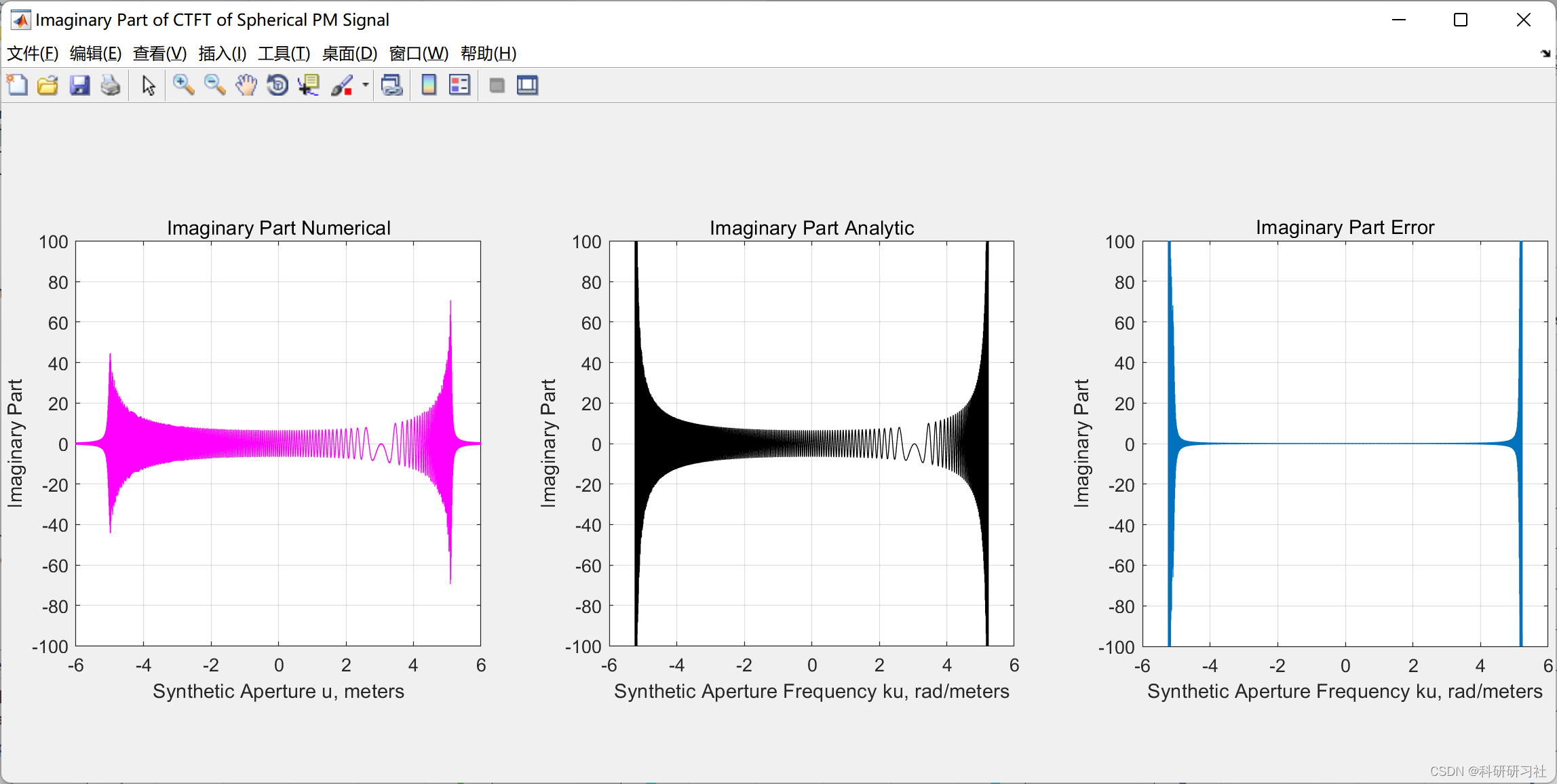
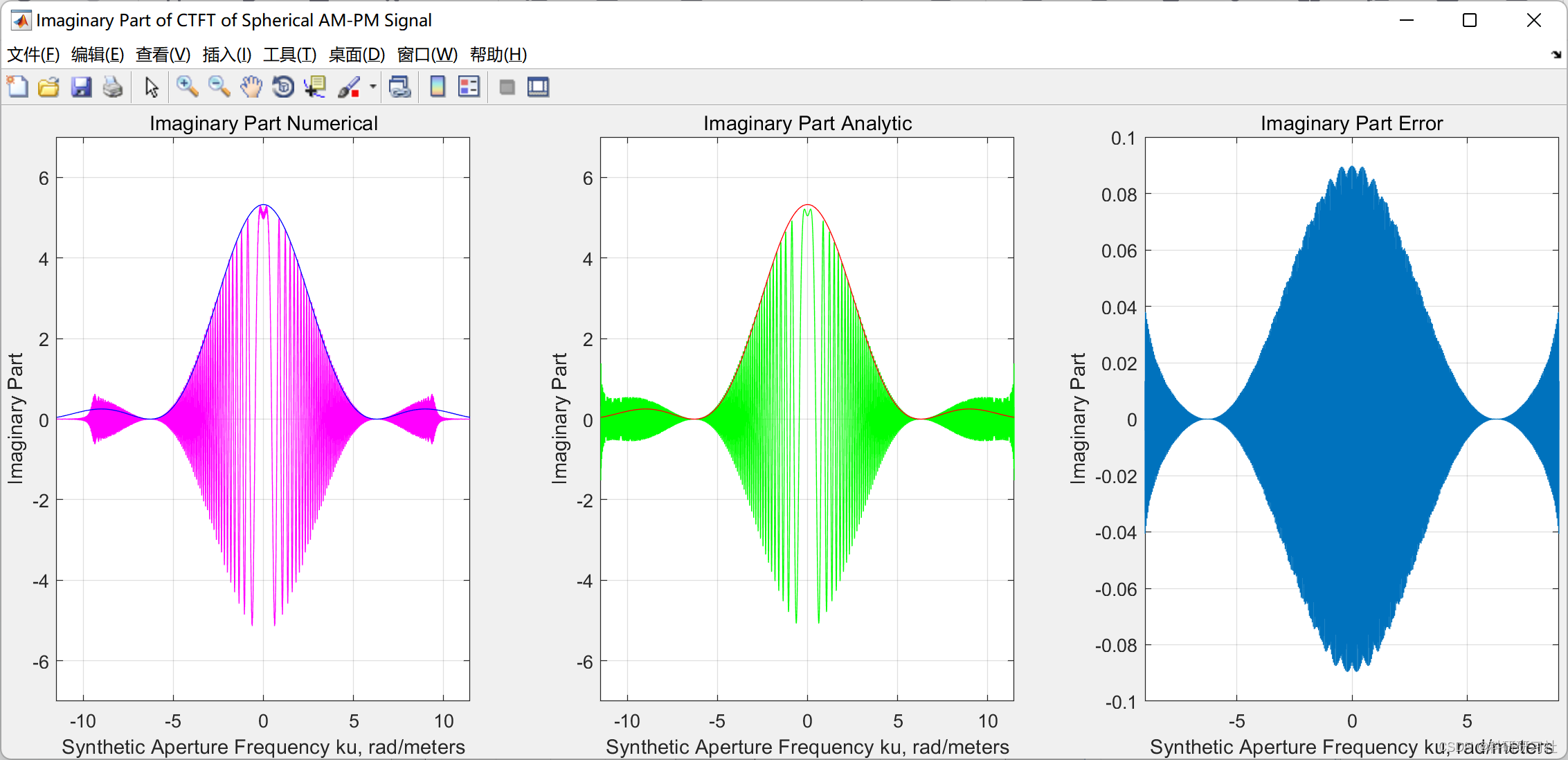
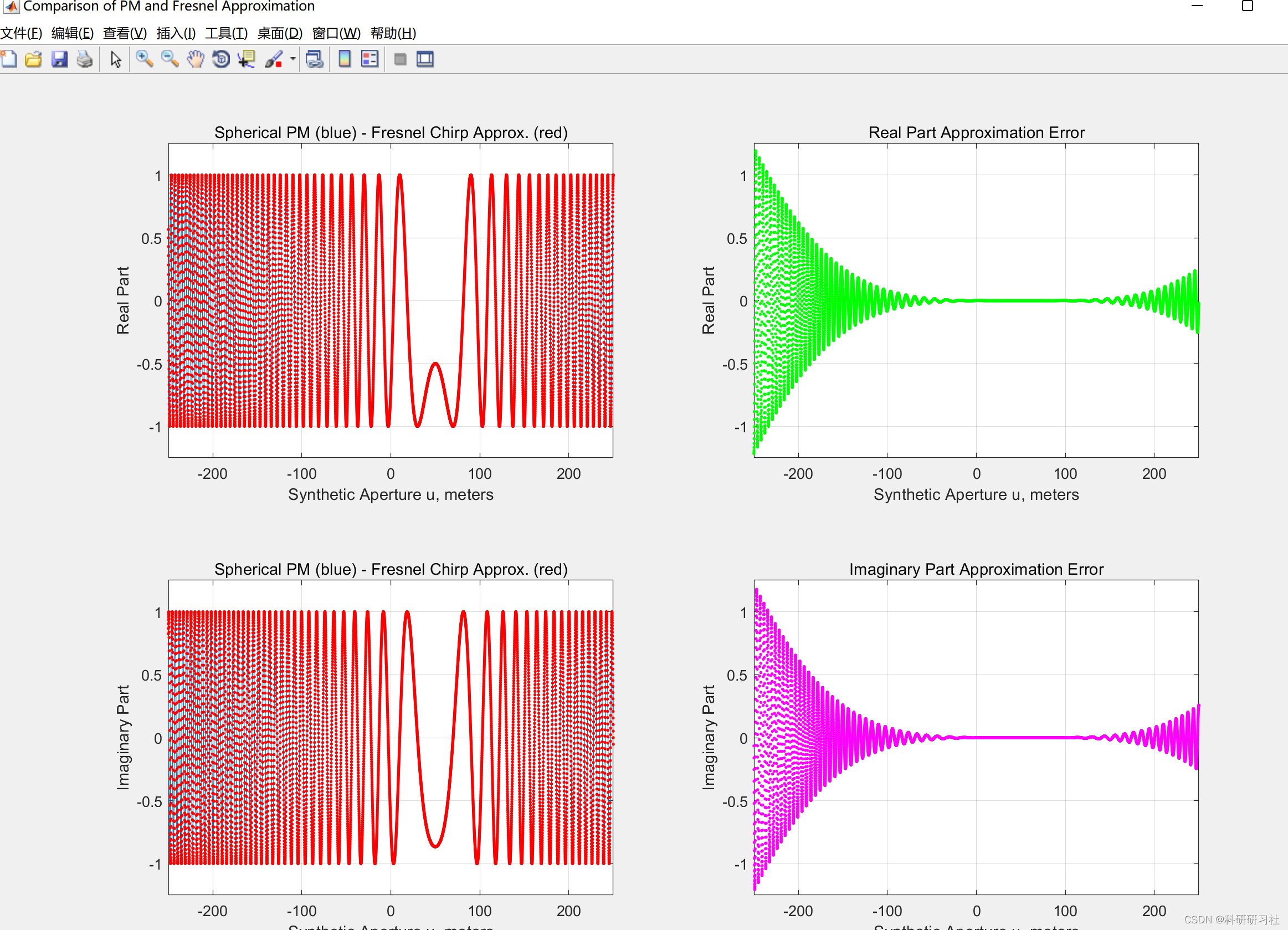
- 计算 AM-PM 和 PM 球面 SAR 信号的 CTFT,包括数值和使用稳态相位近似 (SPA) 方法。
- 几个小的代码改进。
基于优化算法的 SAR 信号处理研究
摘要
随着视频监控技术的不断演进,全数字网络视频监控时代已经到来。然而,现有的数字监控产品如IPC(网络摄像机)和NVR(网络视频录像机)在恶劣天气条件下或受技术限制时,往往无法提供理想的视频图像质量。这不仅影响了图像的识别、取证和事件分析能力,也限制了监控系统的实际应用效果。因此,对图像信号处理技术的研究和应用显得尤为重要。本文聚焦于SAR(合成孔径雷达)信号处理,旨在通过优化算法提升图像质量,克服现有技术的局限性。
1. 引言
SAR作为一种先进的雷达成像技术,具有全天候、全天时成像能力,对于视频监控等领域具有重要意义。然而,SAR信号处理过程中存在诸多挑战,如噪声干扰、图像失真等问题。为解决这些问题,本文提出了一系列基于优化算法的SAR信号处理技术,并对相关算法进行了模块化处理。
2. 目标风光重建算法
本文提供了四种目标风光重建算法,包括2D匹配滤波(波前重建)、时域相关(TDC)、反向投影(BP)和范围堆叠(RS)。这些算法通过不同的数学和物理模型,对SAR信号进行重建和优化,以提高图像质量。
- 2D匹配滤波:利用匹配滤波原理,对SAR信号进行滤波处理,以提取目标信息并重建图像。
- 时域相关:通过计算SAR信号在时域上的相关性,实现目标的检测和定位。
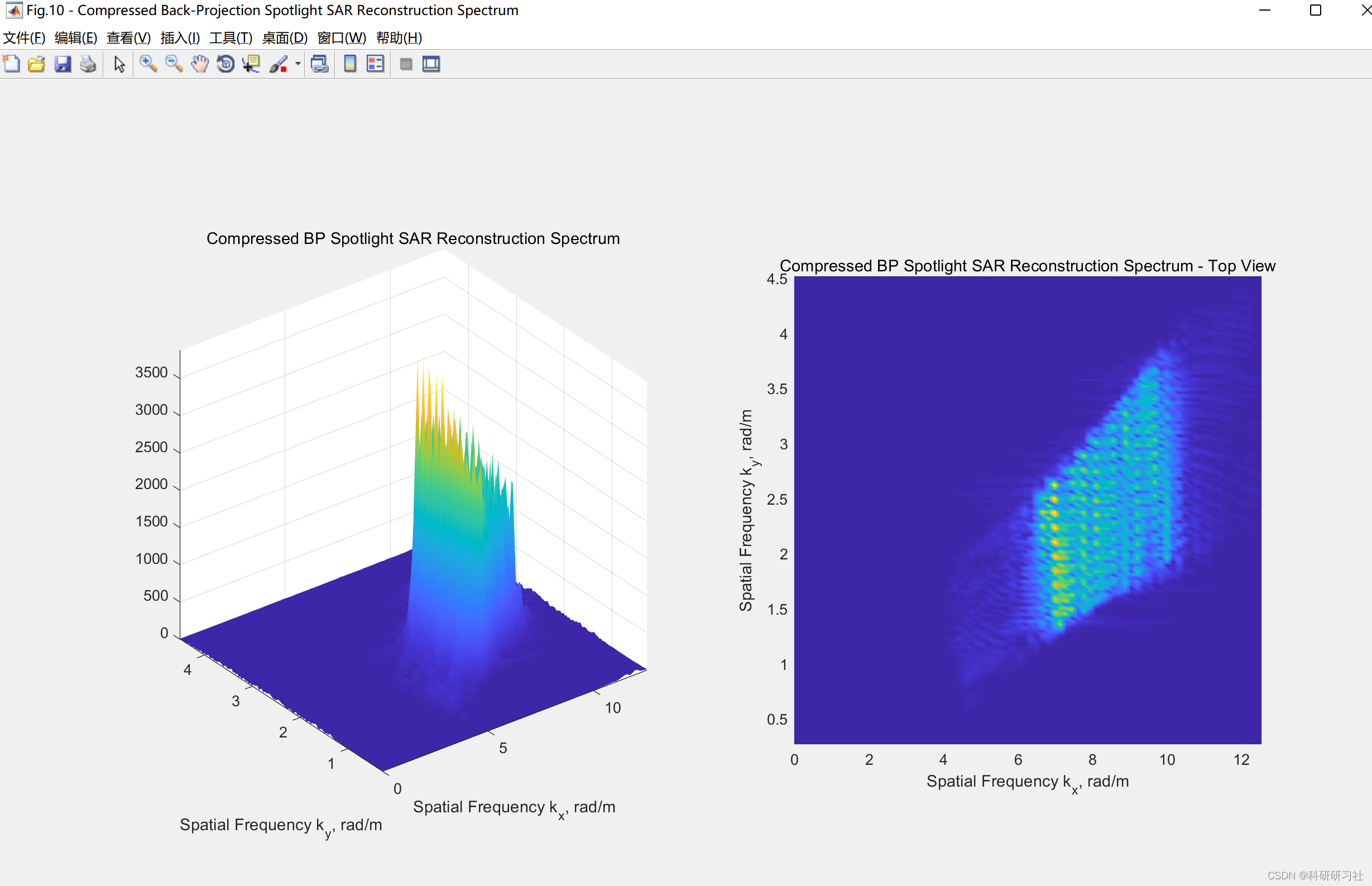
- 反向投影:基于雷达回波数据,通过反向投影算法重建目标的三维图像。
- 范围堆叠:将不同角度的SAR图像进行堆叠处理,以提高图像的分辨率和清晰度。
3. 现代渲染命令替换与优化
为了提升SAR信号处理的效率和准确性,本文用现代渲染命令替换了过时的图形命令。这些现代渲染命令不仅提高了处理速度,还清晰地显示了DSP(数字信号处理)操作对SAR信号的影响。
4. 二维插值代码优化
针对(kx,ky)域中间隔不均匀的数据进行二维插值的问题,本文删除了笨拙的代码,并替换为更加简洁和优雅的MatLab代码。这一优化不仅提高了插值的准确性,还降低了计算的复杂度。
5. AM-PM和PM球面SAR信号的CTFT计算
本文计算了AM-PM(幅度-相位调制)和PM球面SAR信号的连续时间傅里叶变换(CTFT),包括数值方法和使用稳态相位近似(SPA)方法。这些方法为理解和分析SAR信号的频域特性提供了有力工具。
6. 代码改进
除了上述主要优化外,本文还对代码进行了若干小的改进,以提高代码的可读性和可维护性。这些改进包括变量命名规范化、代码结构优化等。
7. 结论
本文提出的基于优化算法的SAR信号处理技术在提高图像质量、克服恶劣天气条件影响等方面具有显著优势。通过模块化处理、现代渲染命令替换、二维插值代码优化以及CTFT计算等方法,本文成功提升了SAR信号处理的效率和准确性。未来,我们将继续深入研究SAR信号处理领域的新技术和新方法,以推动视频监控技术的进一步发展。
2 BP神经网络:通过反投影算法进行脉冲聚光灯 SAR 模拟和重建


3 通过距离堆叠算法进行脉冲聚光灯 SAR 模拟和重建
4 通过 TDC 算法进行脉冲聚光灯 SAR 模拟和重建
5 通过二维匹配滤波进行脉冲聚光灯 SAR 仿真和重建(波前重建)
6 聚光SAR PM球形信号的CTF

7 AM - PM Stripmap SAR 信号的 CTFT
数字图像的噪声主要来源于图像的获取(数字化过程)和传输过程。图像传感器的工作情况受各种因素的影响,如图像获取中的环境条件和传感元器件自身的质量。例如,使用CMOS照相机获取图像,光照程度和传感器温度是生成图像中产生大量噪声的主要因素。同时当信号经过ADC时,又会引人其他一些噪声。这些噪声会使图像整体变的模糊,而且丢失很多细节,令人眼难以接受。所以需要对图像进行去噪处理,以去除这些干扰。
传统的空间去噪方法有均值滤波和中值滤波。均值滤波能够有效地平滑噪声,但同时会将边缘变模糊。为尽量避免这个问题,通常用较小的滑窗(如3×3像素或5×5像素)对图像进行操作。中值滤波法与均值滤波法操作过程类似,所不同的是中值滤波法用滑窗内所有像素值的中间值代替滑窗中心的像素值。同样,这种方法在平滑噪声的同时将使边缘模糊,并会丢失细小的线性特征。5×5像素的中值滤波器将导致可观的边缘模糊。
传统的空间去噪方法都是在RGB彩色空间中进行的,需要三维的图像数据,对RGB三基色分别进行滤波,需要完整的RGB三色值,即需要对bayer型模式的数据进行内插之后的图像。这种方法虽然能够提高滤波效果,但是会占用过多的硬件资源,鉴于此,有人提出一种基于bayer型模式的双边自适应滤波器。该滤波器仅需对二维灰度图像进行滤波处理,它的硬件资源消耗可以减小为前者的1/3。双边自适应滤波器不仅对各类噪声有良好的滤除能力,还能使图像中的细节得到很好保留。
部分理论引用网络文献,如有侵权请联系删除。
8 Matlab代码实现
%% Example 1 - Spotlight SAR with Hamming Window - Figures 2.13.a,b,c,d.
%% Workspace Initialization
clc; clear; close all;
%% Radar System Parameters
c = 3e8; % propagation speed
fc = 300e6; % frequency in Hz.
lambda = c/fc; % Wavelength
k = 2*pi/lambda; % Wavenumber
Xc = 500; % Range distance to center of target area
Y0 = 100;
Yc = 0;
L = 100; % Half-size of synthetic aperture.
%% Signal Definition.
sigma_n = 1;
xn = Xc;
yn1 = 0;
yn2 = 60;
du = 0.2; % sample spacing in u domain should be <=pi/2/k = lambda/4
M = 2*ceil(L/du); % number of samples on aperture
u = du*(-M/2:M/2-1); % synthetic aperture array
dku = 2*pi/(M*du); % sample spacing in ku domain
ku = dku*(-M/2:M/2-1); % ku array
y = u;
% Define the PM Spherical Signals:
sn1 = sigma_n*exp(-1i*2*k*sqrt(xn^2 + (yn1-u).^2));
sn2 = sigma_n*exp(-1i*2*k*sqrt(xn^2 + (yn2-u).^2));
% Hamming Window Function in the SA domain u:
an = abs(u)<=L;
indices = find(an==1);
win = hamming(length(indices)).';
an1 = zeros(1,length(u));
an1(1,indices) = win;
% Define the AM-PM Signals:
sn1_lim = sn1.*an1;
sn2_lim = sn2.*an1;
%% Plot the AM-PM Spherical Signals and their DFT.
h1 = figure('NumberTitle', 'off','Name','Fig. 2.13.a & c. - Spherical AM-PM Signal in aperture u-domain', ...
'Position', [100 0 1400 500]);
subplot(1,2,1);
plot(u,real(sn1_lim))
line([yn1 yn1], [-1.1 1.1],'Color','g');
axis([-250,250,-1.25,1.25]);
xlabel('Synthetic Aperture (Slow-Time) u (m)');
ylabel('\Ree[s_{n1} (t,u)]');
grid on
subplot(1,2,2);
plot(u,real(sn2_lim));
line([yn2 yn2], [-1.1 1.1],'Color','g');
axis([-250,250,-1.25,1.25]);
xlabel('Synthetic Aperture (Slow-Time) u (m)');
ylabel('\Ree[s_{n2} (t,u)]');
grid on
tightfig;
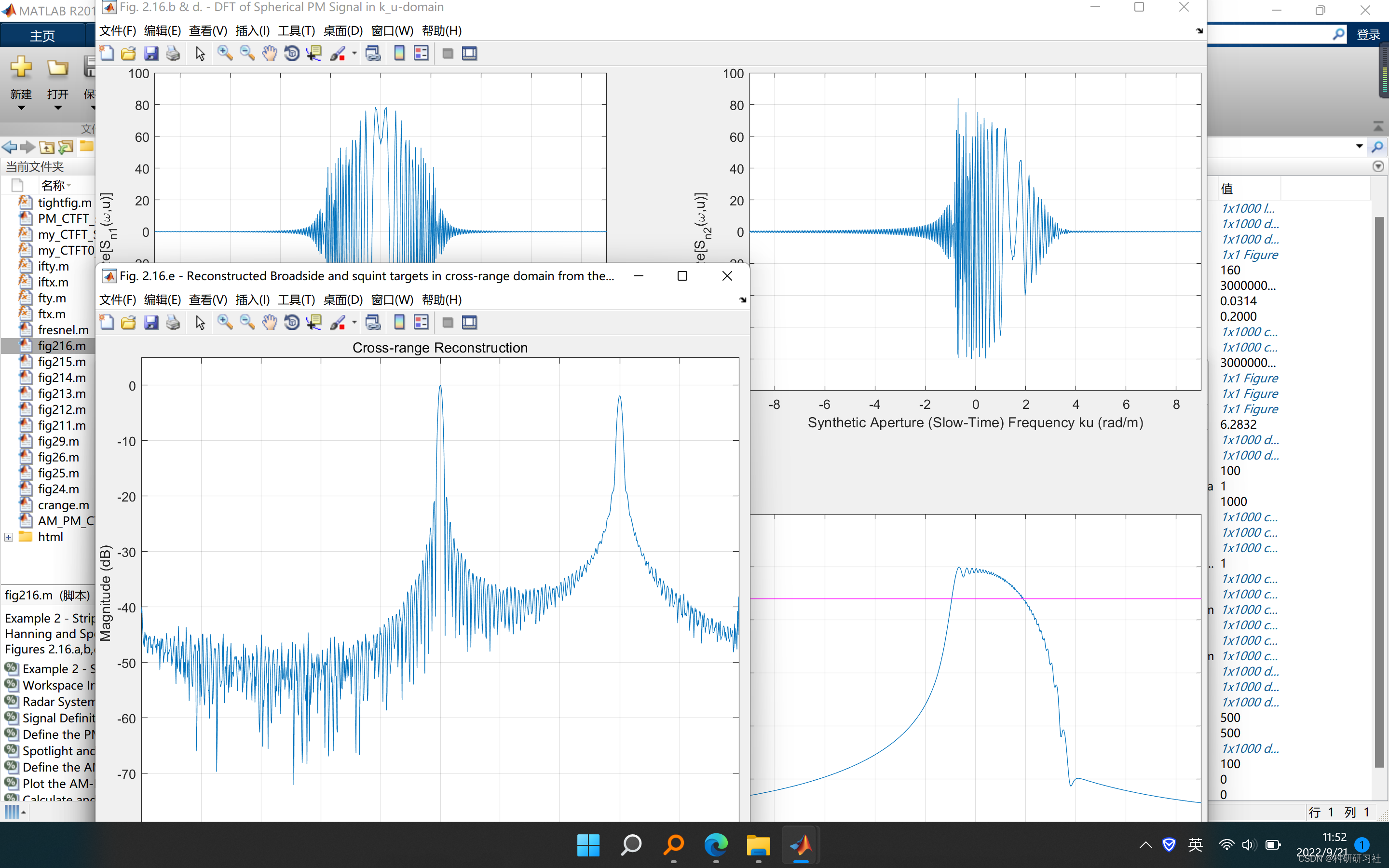
%% Calculate and plot the DFT of sn1(t,u)
Sn1 = ftx(sn1_lim);
h2 = figure('NumberTitle', 'off','Name','Fig. 2.13.b & d. - DFT of Spherical PM Signal in k_u-domain', ...
'Position', [100 0 1200 1100],'Visible','off');
subplot(2,2,1)
plot(ku,real(Sn1));
grid on;
axis([-9 9,-80 80]);
xlabel('Synthetic Aperture (Slow-Time) Frequency k_u (rad/m)');
ylabel('\Ree[S_{n1}(\omega,u)]');
subplot(2,2,3)
plot(ku,10*log10(1/max(abs(Sn1))*abs(Sn1)));
hold on;
line([-9 9] , [-3 -3],'Color','m');
ylim([-25 5]);
xlim([-9, 9]);
xlabel('Synthetic Aperture (Slow-Time) Frequency k_u (rad/m)');
ylabel('\Ree[S_{n1}(\omega,u)] in dB');
grid on;
%% Calculate and plot the DFT of sn2(t,u)
Sn2 = ftx(sn2_lim);
subplot(2,2,2)
plot(ku,real(Sn2));
grid on;
axis([-9 9,-80 80]);
xlabel('Synthetic Aperture (Slow-Time) Frequency ku (rad/m)');
ylabel('\Ree[S_{n2}(\omega,u)]');
subplot(2,2,4)
plot(ku,10*log10(1/max(abs(Sn2))*abs(Sn2)));
line([-9 9] , [-3 -3],'Color','m');
ylim([-25 5]);
xlim([-9,9]);
xlabel('Synthetic Aperture (Slow-Time) Frequency ku (rad/m)');
ylabel('\Ree[S_{n2}(\omega,u)] in dB');
grid on;
set(h2,'Visible','on')
tightfig;
%% Cross Range Reconstruction
% NOTE: ku array corresponds to baseband Doppler domain
s = sn1_lim + sn2_lim;
S = ftx(s);
kx = 4*k^2 - ku.^2;
kx = sqrt(kx.*(kx > 0)); % kx array
S0 = exp(-1i*kx*Xc - 1i*ku*Yc); % reference signal
F = S.*conj(S0); % Slow-Time Matched Filtering
f = ifty(F);
f = f/max(abs(f));
%% Plot the Reconstructed Cros-Range Profile
h3 = figure('NumberTitle', 'off','Name','Fig. 2.13.e - Reconstructed Broadside and squint targets in cross-range domain from their spotlight SAR signal', ...
'Position', [100 0 800 600]);
plot(y,20*log10(abs(f))) % also try "real" and "imag" parts of "f" array
xlabel('Cross-range y, meters')
ylabel('Magnitude (dB)')
title('Cross-range Reconstruction')
axis([-L,L,-80, 5])
grid on;
tightfig;