机器学习之贝叶斯分类器和混淆矩阵可视化

贝叶斯分类器

1 贝叶斯分类器

1.1 概念

贝叶斯分类器是基于贝叶斯定理构建的分类方法，它通过计算后验概率来对数据进行分类。

1.2算法理解

在这里插入图片描述

P(A|B) 是在事件B发生的条件下事件A发生的概率，称为A的后验概率。
P(B|A) 是在事件A发生的条件下事件B发生的概率。
P(A)是事件A发生的概率，称为A的先验概率。
P(B)是事件B发生的概率。

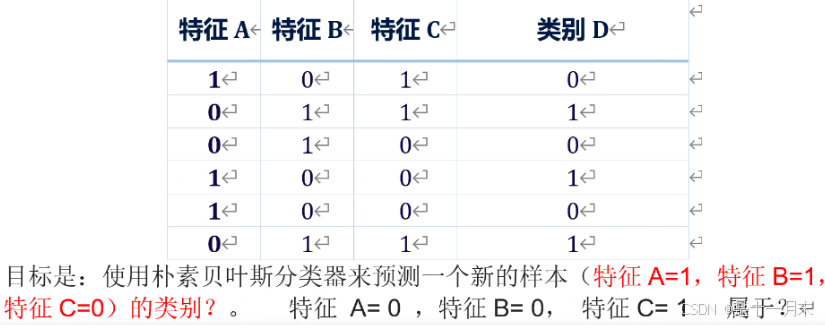
在这里插入图片描述

现在，我们使用朴素贝叶斯牙类器莱计算给定特征值下每个类别的后验率:
P(D=0|A=1,B=1,C=0)=P(D=0)P(A=1ID=0)P(B=1|D=0)P(C=0|D=0)=0.50.6670.3330.667=0.08335583549429845
P(D=1|A=1,B=1,C=0)=P(D=1)P(A=1|D=1)P(B=1|D=1)P(C=0ID=1)0.50.3330.6670.333=0.037499999999999996

1.3 算法导入

from sklearn.naive_bayes import MultinomialNB

1.4 函数

MultinomialNB()
fit(x_tr,y_tr)
predict(x_tr)

2 混淆矩阵可视化

2.1 概念

混淆矩阵（Confusion Matrix），也称为错误矩阵，是一种特别适用于监督学习的评估分类模型性能的工具，尤其是在分类问题中。混淆矩阵展示了实际类别与模型预测类别之间的关系。

2.2 理解

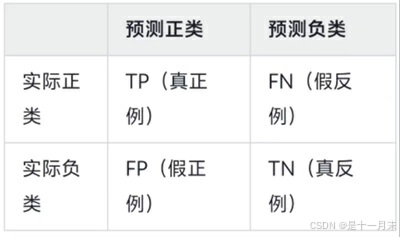
在这里插入图片描述

TP（True Positive）：正确预测到的正类样本数。
FN（False Negative）：实际为正类但预测为负类的样本数。
FP（False Positive）：实际为负类但预测为正类的样本数。
TN（True Negative）：正确预测到的负类样本数。

基于混淆矩阵，可以计算出以下几种性能指标：

准确率（Accuracy）：(TP + TN)/(TP + TN + FP + FN)
精确率（Precision）：TP/(TP + FP)
召回率（Recall）或真正例率（True Positive Rate, TPR）：TP/(TP + FN)
F1分数（F1 Score）： 2 *(Precision * Recall)/(Precision + Recall)
假正例率（False Positive Rate, FPR）：FP/(FP + TN)

2.3 函数导入

from sklearn.metrics import confusion_matrix

2.4 函数及参数

metrics.classification_report(y_te,te_pr,digits=6)

y_te，已知道结果类别
te_pr，训练模型预测的结果类别
digits=6，结果保留的小数点

2.5 绘制函数

代码展示：

def cm_plot(y,y_pr):
    cm = confusion_matrix(y,y_pr)
    plt.matshow(cm,cmap=plt.cm.Blues)
    plt.colorbar()
    for x in range(len(cm)):
        for y in range(len(cm)):
            plt.annotate(cm[x,y],xy=(y,x),horizontalalignment='center',verticalalignment='center')
            plt.ylabel('TRUE label')
            plt.xlabel('PREDICTED label')
    return plt

3 实际预测

3.1 数据及理解

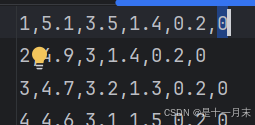
第一列为次序，需要删除，最后一列为结果类别，其他为特征数据。
在这里插入图片描述

3.2 代码测试

代码展示：

import pandas as pd
from sklearn.naive_bayes import MultinomialNB
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn import metrics

def cm_plot(y,y_pr):
    cm = confusion_matrix(y,y_pr)
    plt.matshow(cm,cmap=plt.cm.Blues)
    plt.colorbar()
    for x in range(len(cm)):
        for y in range(len(cm)):
            plt.annotate(cm[x,y],xy=(y,x),horizontalalignment='center',verticalalignment='center')
            plt.ylabel('TRUE label')
            plt.xlabel('PREDICTED label')
    return plt

data = pd.read_csv('iris.csv')
data = data.drop(['1'],axis=1)
x = data.drop(['0'],axis=1)
y = data['0']

x_tr,x_te,y_tr,y_te = \
    train_test_split(x, y, test_size=0.2,random_state=0)

by = MultinomialNB()
by.fit(x_tr,y_tr)
tr_pr = by.predict(x_tr)
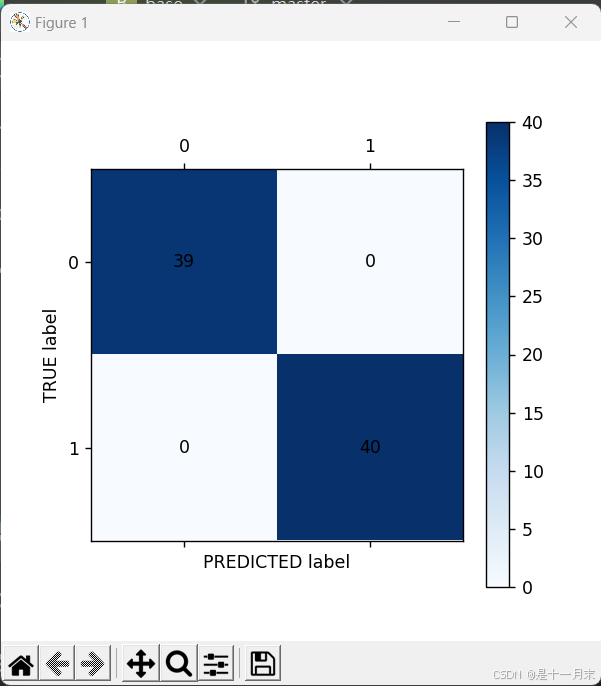
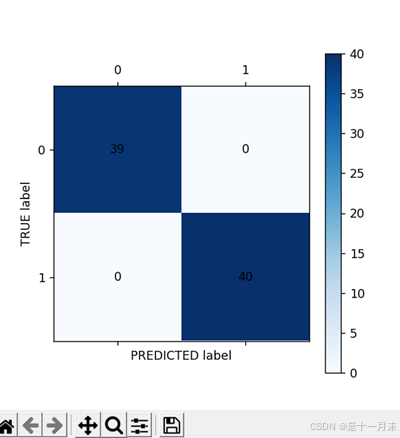
cm_plot(tr_pr,y_tr).show()
te_pr = by.predict(x_te)
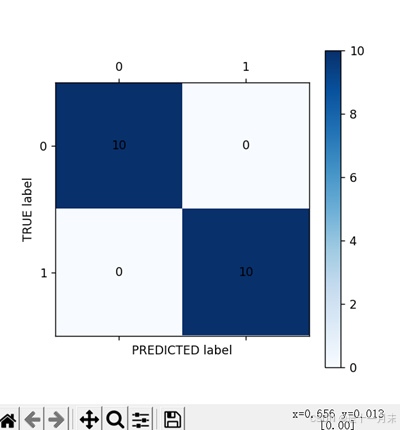
cm_plot(te_pr,y_te).show()
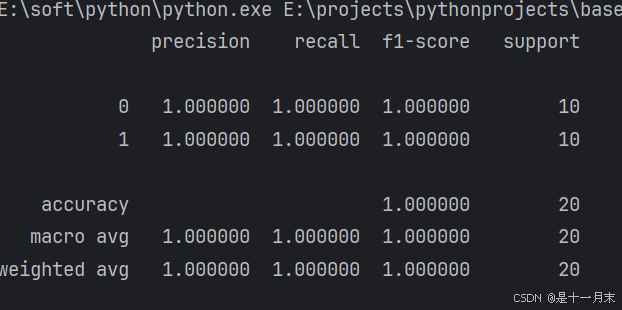
print(metrics.classification_report(y_te,te_pr,digits=6))