✨个人主页欢迎您的访问


在机器学习的世界里,支持向量机(Support Vector Machine,简称SVM)是一个强大且深受喜爱的算法。它在分类问题中展现出了卓越的性能,尤其是在数据集规模较小或数据分布较复杂的情况下,SVM的表现常常让人惊叹。本篇博客将带领你深入了解SVM的原理、实现过程以及在实际问题中的应用。
✨什么是支持向量机(SVM)✨
支持向量机是一种监督学习算法,主要用于分类问题,但也可以扩展到回归问题。它的核心思想是通过寻找一个超平面(hyperplane),使得该超平面能够最有效地分割数据,最大化边界(margin),从而实现对数据的分类。
核心概念:
- 超平面(Hyperplane):在二维空间中,超平面是一个线,三维空间中是一个平面,而在高维空间中,超平面是一个n-1维的平面。支持向量机的目标是找到一个超平面,能够将不同类别的样本分开。
- 边界(Margin):边界是指样本点到超平面的距离。SVM通过最大化类别之间的边界来提高模型的泛化能力。
- 支持向量(Support Vectors):支持向量是指位于边界上或距离边界最近的样本点。这些样本点决定了超平面的最终位置,因而对分类结果有直接影响。
✨SVM的工作原理✨
SVM的工作原理可以从以下几个步骤来理解:
-
找到最佳分割超平面:假设我们有两个类别的数据,SVM试图在这两个类别之间找到一个超平面,使得每个类别的数据点尽可能远离这个平面。为了实现这一点,SVM会最大化两类数据点与超平面之间的间隔(margin)。最大间隔通常会使得模型对新的、未见过的数据点具有更好的分类能力。
-
最大化间隔:SVM的优化目标是最大化边界,即在保证两类样本被正确分类的情况下,使得支持向量到超平面的距离尽可能大。这个间隔越大,模型的泛化能力就越强。
-
处理非线性可分问题:如果数据不是线性可分的(即无法通过一条直线或超平面将数据完全分开),SVM通过**核函数(Kernel Function)**将数据映射到更高维的空间,在高维空间中,数据有可能变得线性可分。常见的核函数有:
- 线性核函数:当数据本身线性可分时,使用线性核是最有效和计算成本最低的方法。
- 多项式核函数:当数据有多项式关系时,选择多项式核可以较好地处理高维特征。
- 径向基函数(RBF)核函数:RBF核非常适用于大部分复杂的非线性数据,特别是当数据分布未知时。
- Sigmoid核:适用于模拟神经网络行为,但参数调节和应用场景需要小心。
- 拉普拉斯核:当数据噪声较多时,拉普拉斯核的曼哈顿距离可能更加鲁棒。
- 傅里叶核和切比雪夫核:适合周期性特征的信号处理应用。
-
软间隔(Soft Margin):在实际应用中,数据通常不可能完美分割。这时,我们可以允许一些点位于错误的分类区域内(即在边界的另一侧),从而引入了一个叫做“软间隔”的概念。软间隔的引入可以通过一个叫做惩罚因子的超参数来控制,通常通过调整惩罚因子来平衡模型复杂度和分类精度。
✨SVM的数学公式✨
SVM的目标是通过优化问题来寻找最佳的超平面。我们可以通过以下几个步骤来推导出SVM的目标函数。
假设我们有一个训练集 {(xi,yi)},其中 xi是输入特征,yi是输出标签,且 yi∈{−1,+1}(二分类)。我们希望找到一个超平面,使得该平面能够最大化边界,满足以下条件:
1.线性决策超平面方程:
其中,ww 是超平面的法向量,bb 是偏置项。
2.为了确保类别的正确分类,我们希望每个样本 xi满足:
这表示对于每个样本,其距离超平面的距离至少为 1。 最大化边界,即最大化 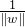
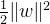
3.综合这些条件,SVM的优化问题可以转化为:
同时,满足:
✨SVM的优势与应用✨
优势
- 高效性:SVM对于小规模数据集非常有效,且理论上可以做到全局最优解。
-
泛化能力强:通过最大化边界,SVM通常能够构建出对新数据具有良好泛化能力的模型。
- 适用于高维数据:SVM尤其擅长处理高维数据集,例如文本分类、图像识别等领域。
应用场景
- 文本分类:SVM广泛应用于垃圾邮件过滤、情感分析等文本分类任务。通过使用核函数,可以在高维的特征空间中取得较好的分类效果。
- 图像识别:在图像处理领域,SVM可以用于人脸识别、物体检测等任务。通过有效地处理图像的高维特征,SVM能够提供很好的分类性能。
- 生物信息学:在基因数据分析中,SVM常被用于疾病分类或基因表达数据的分类任务。
✨实际操作:SVM的Python实现✨
下面是使用scikit-learn库实现一个简单的SVM分类器的例子。
# 导入必要的库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
# 加载数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 创建SVM分类器
svm_clf = SVC(kernel='linear', C=1)
# 训练模型
svm_clf.fit(X_train, y_train)
# 进行预测
y_pred = svm_clf.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型的准确率为:{accuracy:.2f}")
在这个例子中,我们使用了scikit-learn中的鸢尾花数据集,并使用线性核的SVM进行分类。C是SVM中的惩罚参数,控制分类间隔的宽度,kernel='linear'表示我们使用线性核函数。
✨总结✨
支持向量机(SVM)是一种非常强大的机器学习算法,尤其适用于小规模和高维数据的分类问题。它通过最大化数据之间的间隔,能够提供良好的分类效果,并且具有很强的理论基础。在实际应用中,通过合理的核函数和参数调节,SVM可以解决复杂的分类任务。无论是在文本分类、图像识别,还是生物数据分析等领域,SVM都展现了它的广泛应用前景。
希望本文能帮助你理解支持向量机的基本原理与实现方法,激发你在实际项目中运用SVM的兴趣。如果你对SVM或机器学习的其他方面有任何问题,欢迎留言交流!