哈利·波特考试（c/c++）

题解往下划拉

写在前面的碎碎念：我在上一道题说我理不清楚，花里胡哨地给int改名，做一个图要定义俩结构体三个函数，然后先插边再插图的。然后再学习下一节的时候感觉自己理清了是什么意思（但还是不理解那么费劲干嘛）,然后就用那个麻烦的办法，就是按照老师PPT写了哈利波特考试这道题，结果
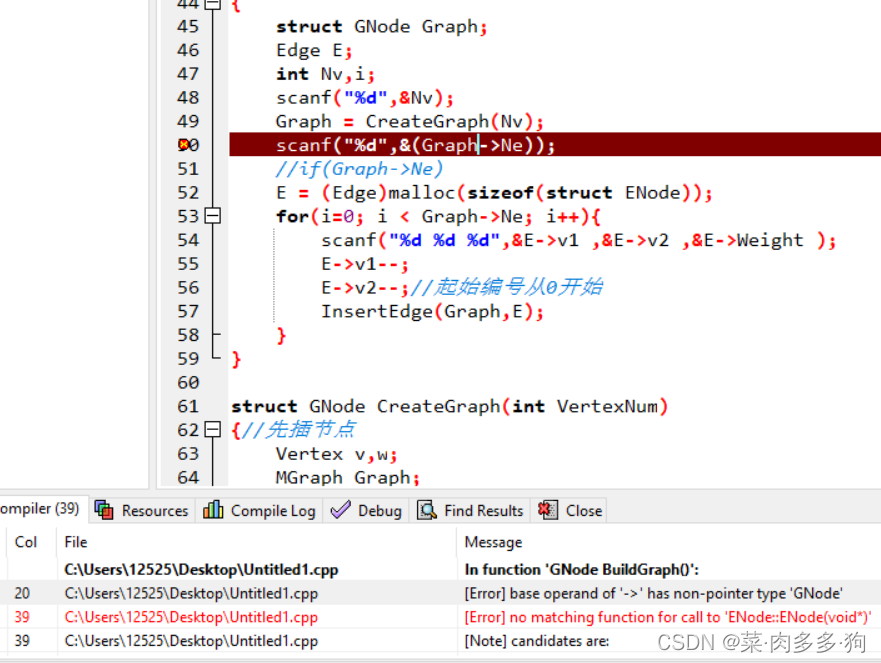
在这里插入图片描述
我真的不理解，我就是按老师PPT打的。我改来改去，吧输入揉到Create里，然后下面又报错了，基本上意思就是我的Graph不能用->。后来我发现发了问题，我以为的照着写并没有照着写。

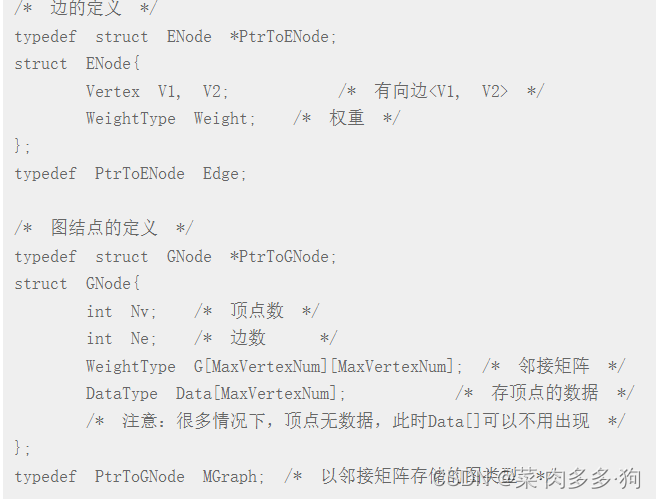
我自作聪明的把结构体改个名，再把改的名字再改个名的操作直接用一个typedef。忽略了把MGraph和Edge改成指针。

7-25 哈利·波特考试

（抱歉标题在这里才出现）
在麦格教授的变形课上，哈利·波特正在学习如何通过一些咒语将一个物体变成另一个物体。他已经知道了，要把猫变成老鼠，人们可以说！要扭转效果，只需说！从形式上讲，在对象A和对象B之间转换的变形咒语被称为如果有两个咒语，并且分别将A变成B，反之亦然。docamodecamoSdoSdeS

在某些情况下，定义短切咒语以使变形更容易。例如，假设将猫变成老鼠的咒语是，而将老鼠变成胖鼠的咒语是，那么将猫变成胖鼠可能会说！或者，如果一个射击切割法术被定义为，人们可能会通过说！docamodofamodocamodofamocafamdocafam

时间过得很快，期末考试即将到来。在变形考试结束时，学生将被要求向麦格教授展示几个从他们带到教室的初始物体转换而来的物体。他们每个人只能携带1个物体。

现在哈利来找你寻求帮助：他需要一个程序来选择他必须参加考试的对象，这样他要说的任何咒语的最大长度就会被最小化。例如，如果猫、老鼠和胖鼠是考试中仅有的三个对象，那么老鼠就是哈利应该采取的对象，因为老鼠需要6个字母的咒语才能把老鼠变成猫或胖老鼠。猫不是一个好的选择，因为它至少需要7个字母的咒语才能把它变成一只胖老鼠。出于同样的原因，哈利一定不能吃胖鼠。

输入规格：
每个输入文件包含一个测试用例。对于每种情况，第一行包含两个正整数N (≤100）和M，分别是考试中涉及的对象总数和要测试的法术数。为简单起见，对象编号从 1 到N.然后M行紧随其后，每行包含3个整数，由空格分隔：两个对象的编号，以及它们之间转换的咒语的长度。

输出规格：
对于每个测试用例，用一行打印哈利必须参加考试的物体的编号，以及他可能要说出的咒语的最大长度。数字必须用空格分隔。

如果仅通过获取一个对象无法完成所有变形，则只需输出 0 即可。如果解决方案不是唯一的，则输出具有最小数字的那个。

示例输入：
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
示例输出：
4 70

#include<stdio.h>
#include<stdlib.h>
#define INF 65535
#define MaxVertexNum 100

typedef int WeightType;
typedef int Vertex;

//图节点 
typedef struct GNode *PtrtoGNode; 
struct GNode{
	int Nv;//顶点数
	int Ne;//边数 
	WeightType G[MaxVertexNum][MaxVertexNum];
};
typedef PtrtoGNode MGraph;

//图边 
typedef struct ENode *Edge;
struct ENode{
	Vertex v1,v2;//v1v2有向边
	WeightType Weight; 
};

MGraph BuildGraph();

MGraph CreateGraph(int VertexNum);

void InsertEdge(MGraph Graph,Edge E);

void FindAnimal(MGraph Graph);

void Floyd(MGraph Graph,WeightType D[][MaxVertexNum]);

WeightType FindMaxDist(WeightType D[][MaxVertexNum],int i,int N);

int main()
{
	MGraph G = BuildGraph();
	FindAnimal(G);
	return 0;
}

MGraph BuildGraph()
{
	MGraph Graph;
	Edge E;
	int Nv,i;
	scanf("%d",&Nv);
	Graph = CreateGraph(Nv);
	scanf("%d",&(Graph->Ne));
	if(Graph->Ne){
		E = (Edge)malloc(sizeof(struct ENode));
		for(i=0; i < Graph->Ne; i++){
			scanf("%d %d %d",&(E->v1 ),&(E->v2 ),&(E->Weight ));
			E->v1--;
			E->v2--;//起始编号从0开始
			InsertEdge(Graph,E); 
		}	
	}
	return Graph;
}

MGraph CreateGraph(int VertexNum)
{//先插节点 
	Vertex v,w;
	MGraph Graph;
	Graph = (MGraph)malloc(sizeof(struct GNode));
	Graph->Nv = VertexNum;
	Graph->Ne = 0;
	for(v=0; v < Graph->Nv; v++)
		for(w=0; w < Graph->Nv; w++)
			 Graph->G[v][w] = INF;
	return Graph;
}

void InsertEdge(MGraph Graph,Edge E)
{
	Graph->G[E->v1][E->v2] = E->Weight ;
	Graph->G[E->v2][E->v1] = E->Weight ;
}

void FindAnimal(MGraph Graph)
{
	WeightType D[MaxVertexNum][MaxVertexNum],max,min=INF;
	Vertex Animal,i;
	Floyd(Graph,D);
	for(i=0; i < Graph->Nv ;i++){
		max = FindMaxDist(D,i,Graph->Nv);
		if(max == INF){ 
			printf("0\n");
			return;
		}
	    if(min > max){
			min = max;
			Animal = i+1;
		}
	}
	printf("%d %d\n",Animal,min);
}

void Floyd(MGraph Graph,WeightType D[][MaxVertexNum])
{
	Vertex i,j,k;
	for(i=0; i < Graph->Nv; i++){
		for(j=0; j < Graph->Ne ;j++){
			D[i][j] = Graph->G[i][j];
		}
	}
	for(k=0; k < Graph->Nv ;k++)
		for(i=0; i < Graph->Nv ;i++)
			for(j=0; j < Graph->Nv ;j++)
				if(D[i][k]+D[k][j] < D[i][j])
					D[i][j] = D[i][k]+D[k][j];	
}

WeightType FindMaxDist(WeightType D[][MaxVertexNum],int i,int n)
{
	WeightType max=0;
	int j;
	for(j=0; j<n; j++){
		if(i!=j && D[i][j]>max)
			max = D[i][j];
	}
	return max;
}

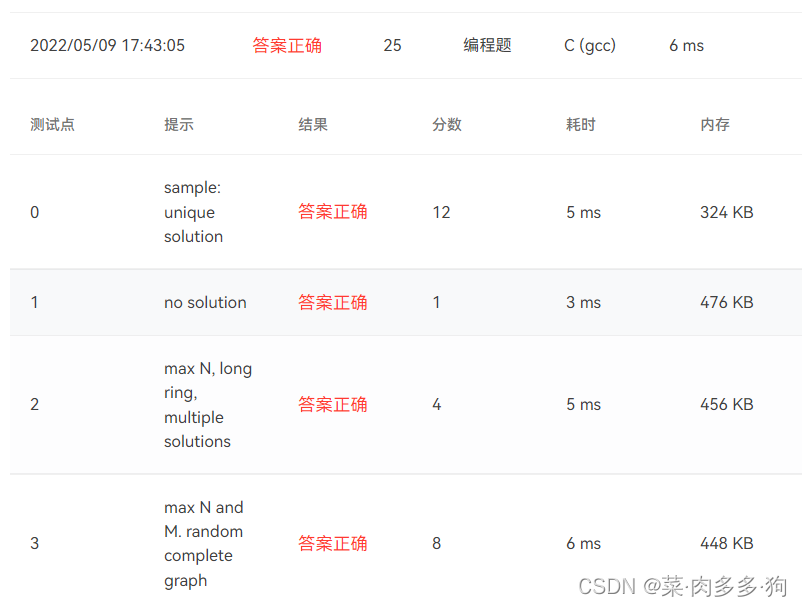
结尾的碎碎念：其实当我编译成功之后并没成功跑出来,出现了各种各样的问题，比如跑出来是0，程序跑死，答案不完全正确，一遍遍检查鼓秋了一个下午才成功。
在这里插入图片描述
写不出来，写出来编译不成功，编译成功跑不出来，跑出来不能那到分，每个环节都很痛苦。一个人在孤军奋战，希望自己能够如愿以偿。

半年之后的更新：其实之前有过想法把自己之前乱七八糟写的题的文章都好好整整（由于懒一直也没搞）。现在倒是觉得留着看自己之前笨拙的思路也不是没有意义（在给自己懒找借口）。不难的道题，Floyd求最短路径，半年前的自己觉得难到不行了hhhh。
需要注意：1.图是无向图，A到B，B也能到A。（之前没仔细读题输出都是0）
2.这个题的描述太考验阅读理解能力了，题目要的不是变到任何动物咒语最短的动物，而是最难变到的那个动物咒语最短的动物（求max的min）。

#include<bits/stdc++.h>
using namespace std;
#define INF 0xcffffff

int main(){
    int n,m;
    cin>>n>>m;
    int map[n][n];
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++) map[i][j]=INF;
    }
    int x,y,w;
    for(int i=0;i<m;i++){
        cin>>x>>y>>w;
        map[x-1][y-1]=w;
        map[y-1][x-1] = w;
    }
    for(int k=0;k<n;k++){
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                if(map[i][k]+map[k][j]<map[i][j]){
                    map[i][j] = map[i][k]+map[k][j];
                }
            }
        }
    }
    int min=INF,max,k,flag=1;
    for(int i=0;i<n;i++){
        max = 0;
        for(int j=0;j<n;j++){
            if(i!=j&&map[i][j]>max) max= map[i][j];
        }
        if(max==INF){
            cout<<"0"<<endl;
            flag=0;
            break;
        }
        if(min>max){
            min = max;
            k = i+1;
        }
    }
    if(flag) cout<<k<<" "<<min<<endl;
    return 0;
}

在这里插入图片描述