柏林噪声与MC

引入

暑假入门Unity后打算做一个类MC的游戏。大家都知道，MC地形几乎是“无限”生成的(实际上有一个特别大的上限值)，人工制作如此庞大的地图必然不现实，内存也无法容纳这么多方块。因此，地形的生成必须得依靠算法实时计算，计算后加载玩家附近的区块，并将结果渲染在画面中。

在MC中，各种地形是比较贴近自然的，那么它具体是依靠怎样的算法生成的呢？其中一个核心就是柏林噪声。

简介

柏林噪声 ( Perlin noise )指由Ken Perlin发明的自然噪声生成算法。它是一个非常常见的游戏开发技术，主要用于随机地图的生成。

噪声(Noise) 实际上就是一个随机数生成器，当然，这是一种伪随机（现实世界中的真随机在计算机中不存在）。我们所看到的那些黑白噪声图，实际上是随机数映射到0和1之间产生的灰度图。随机本身就是不同，那为什么还需要不同的随机？

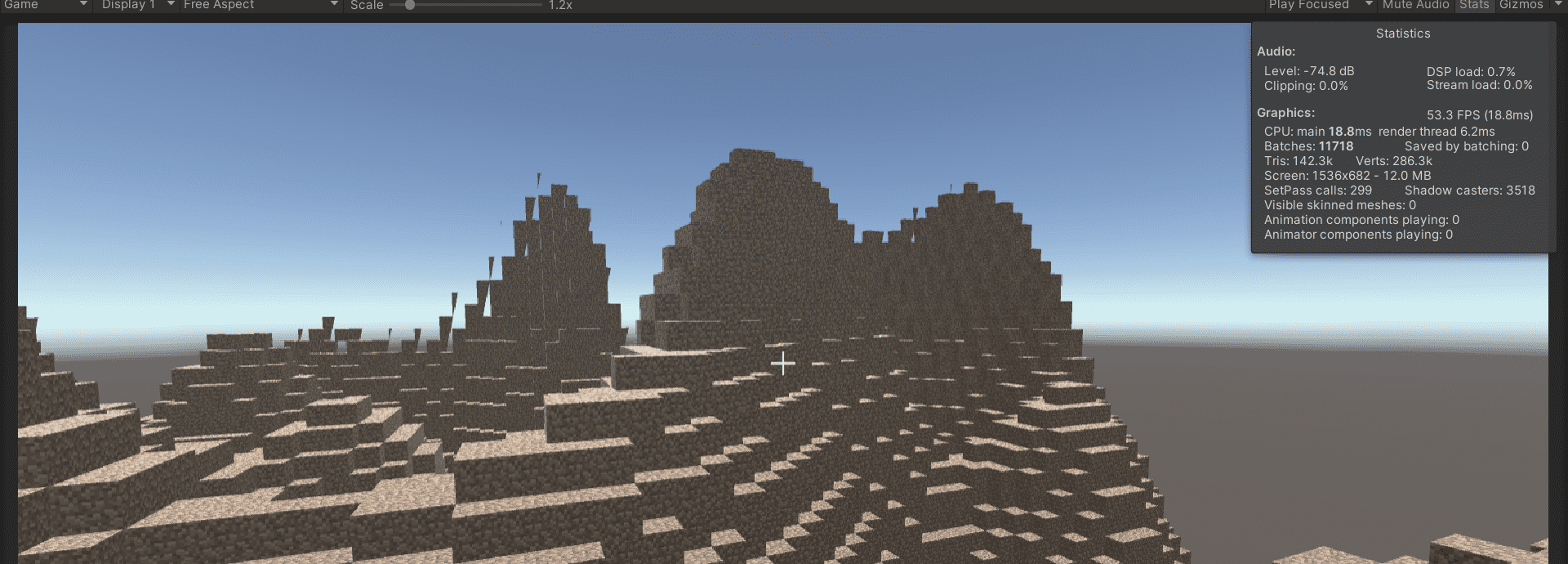
普通噪声（随机数生成器）的问题在于，它实在太过于随机，毫无规律可言。曾经我尝试过在制作的游戏中用随机数生成地形，得到了如下的结果：

随机数地形.png

我们可以发现，用随机数生成的地形起伏非常大，高度非常离散，毫无规律可言，这显然无法达到我们的预期。

柏林噪声基于随机，并在此基础上利用缓动曲线进行平滑插值，使得最终得到噪声效果更加趋于自然。那柏林噪声的表现又如何呢？我们来看看下面这张图：

噪声地形.png

这是我自己用柏林噪声实现的地形，我们可以发现，地形已经变得比较连续/平滑了，效果很Nice！

算法

实现步骤

基于不同的采样空间，柏林噪声可以分为一维、二维和三维，不同维度的算法都很类似，主要经过以下三个步骤：

初始化相关数据，包括排列表(Permutation Table) 和 梯度表(Gradient Table) 等，其中梯度表中元素绝对值的max一般是1；
建立采样空间和参考点。对于一维柏林噪声，采样空间为一个一维的坐标轴，轴上整数坐标位置均有一个点。而对应二维柏林噪声，采样空间为一个二维坐标系，坐标系中横纵坐标为整数的地方均有参考点。三维柏林噪声同理。根据步骤一的两个表格对每一个整数坐标点计算它们的伪随机梯度，该梯度的维数和采样空间维数相同；
对于噪声图上的像素，找到它在晶格上对应的一点，并求出它的参考点的坐标。在一维情况下，参考点为两侧最近的整数点；二维情况下，参考点为组成包围该点的单位正方体的四个点；三维情况下，参考点为组成包围该点的单位立方体的八个点。
对于不同类型的噪声，对采样点在不同空间中，根据最近的参考点的梯度和缓动曲线进行插值计算。

步骤一的意义

首先谈谈为什么要在步骤一生成排列表和梯度表。排列表是一个乱序存放一系列索引值的表，而梯度表是一个存放了一系列随机梯度值的表，两者都具有很强的随机性。在决定一个点的梯度时，需要结合哈希函数，以点的坐标为参数，利用所得的值作为索引，去排列表中取对应的值。所取得的排列表中的值，就是该点在梯度表中对应梯度值的索引。这样解释可能会有些让人摸不着头脑，我们来看一段伪代码。

// 排列表 存放着随机生成的一组数据
int[] perm = {...};

// 梯度表 存放着随机生成的一组数据 一般限定范围是[-1,1]
float[] grad = {...};

// 只有整数点才需要随机指定梯度，以计算非整数点的插值 
// 注：ref为C#语法 相当于C++的引用类型
void Hash(ref int[] gradient, int x, int y) {
    // 通过哈希函数找到排列表的索引
    int permIdx[] = new int[2];
    permIdx[0] = FindIndex(x);
    permIdx[1] = FindIndex(y);

    // 通过排列表索引找到梯度表的索引
    int gradIdx[] = new int[2];
    gradIdx[0] = perm[permIdx[0]];
    gradIdx[1] = perm[permIdx[1]];

    // 在梯度表中找到梯度值 得到了点(x,y)的梯度值
    gradient[0] = grad[gradIdx[0]];
    gradient[1] = grad[gradIdx[1]];
}

这段代码是针对二维柏林噪声的梯度生成方法，通过函数Hash可以得到整数点(x,y) 的梯度值，可能大家比较疑惑，为什么不直接使用快捷的random函数生成随机梯度值呢？因为random的返回值是和调用次数相关的，但是我们希望在每次调用同一个点都能得到相同的梯度值，random就不满足我们的需求了。而建立一个排列表和梯度表能够实现以上要求。

一维柏林噪声

先谈谈最简单的一维情况，下面这张图中，一维的轴是x轴（水平），柏林噪声输出值为y轴（竖直）。我们以两个整数采样点为一个单元，也就是 $A(x_A),B(x_B)(满足x_A,x_B\in Z,x_B-x_A=1)$ 。

而我们待计算的点是 $X (x)$ (即X点的横坐标为x)。

一维柏林噪声图片.png

经过步骤一和步骤二，假设两点的随机初始化梯度（维数为1）分别是 $\vec{AD}=(0.3) \ \vec{BE}=(-0.1)$ ，并且你已经完成步骤三：找到了 $X$ 点附近的整数点 $A, B$ 。如何进行步骤四的插值呢？柏林想到用点积将点 $A, X, B$ 三个点关联起来：

$计算向量\vec{AX} 和 \vec{BX} 的大小，在这里是\vec{AX}=(x-x_A) \ \vec{BX}=(x-x_B)$
将 $\vec{AX}$ 和随机初始化的 $\vec{AD}$ 做点积得到 $dot_1$ ； $\vec{BX}$ 和随机初始化的 $\vec{BE}$ 做点积得到 $dot_2$
根据 $dot_1和dot_2$ 计算X点的输出值，在图中也就是 $y_F=dot_1+k*(dot_2-dot_1),其中k=f(x-x_A)，f为缓动曲线,f一般取f(t)=3t^2-2t^3 或 f(t)=6t^5-15t^4+10t^3$

于是得到了上图中紫色曲线的效果，以上就是一个单元的计算方法

我们为什么要加入缓动曲线呢？缓动曲线是为了增加结果的光滑性，我们来看看两个缓动曲线与正比例函数 $f (t) = t$ 的对比图：（0<x<1)

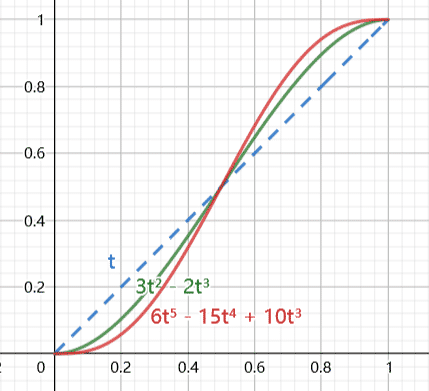
将多个单元连起来，就形成了以下结果(下图横轴中每一个绿点代表一个整数)

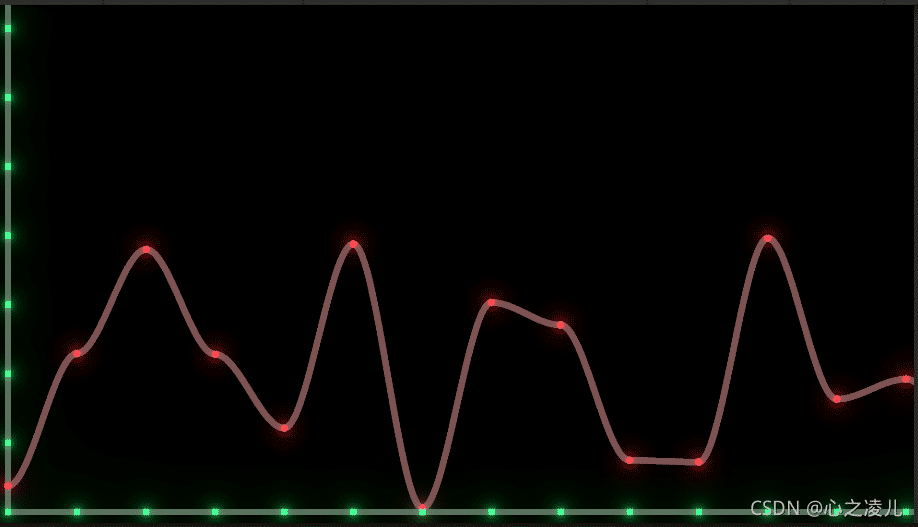
最后，如果梯度表中元素绝对值的max为1，一维柏林噪声返回值的范围应该是[-1,1],感兴趣的小伙伴可以估计一下。

二维柏林噪声

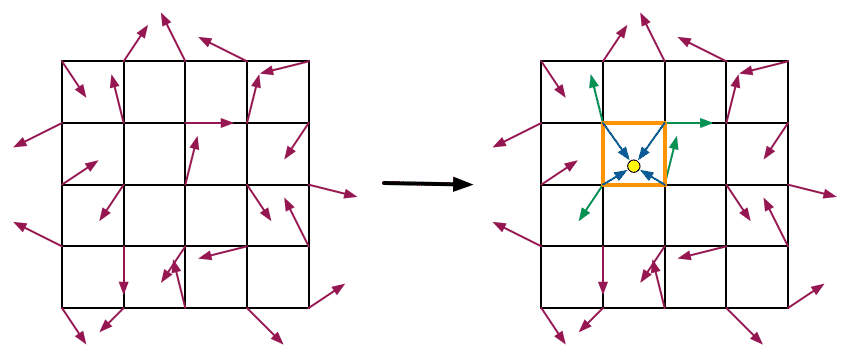
二维柏林噪声需要横/纵坐标，我们可以把输出视作”高度“。如下面的左图，每个小正方形的顶点就是一个整数点，计算柏林噪声的单元就是一个小正方形了（比如下方右图橘黄色标注部分）一维柏林噪声只需要初始化一条线上整数点的梯度，二维则需要计算一个面上整数点的梯度，并且初始化梯度维数为2。

2D柏林噪声.png

梯度初始化完成后，就要进行插值计算了。二维柏林噪声方法与一维差别不大，大家可以和之前提到的一维柏林噪声插值计算的步骤对比。参考下图，设一个正方形单元的四个顶点分别是 $P_0,P_1,P_2,P_3$ ，待求柏林噪声的点是 $P (x, y)$ ，那么计算方法可以是以下步骤(字母遵循下图)：

计算向量 $\vec{P_0P},\vec{P_1P},\vec{P_2P},\vec{P_3P}$ 的大小，记作 $v_0,v_1,v_2,v_3$
将 $\vec{P_iP}$ 和在 $P_i$ 随机初始化的 $\vec{grad_i}$ 做点积得到 $Z_i$ (其中i取遍0，1，2，3)；
插值计算：根据点积结果 $Z_0,Z_3$ 插值得到 $Z_{03}=Z_0-t_0*(Z_3-Z_0)$ ， $Z_1,Z_2$ 插值得到 $Z_{12}$ ,其中， $t_0$ 由缓动曲线 $f(x-x_0)$ 给出。这两次插值相当于在y方向上进行一维插值，得到 $P_{03}和P_{12}$ 的高度；借助这两点，我们又可以继续在x方向进行插值。得到P的柏林噪声值(高度) $Z=Z_{03}-t_1*(Z_{12}-Z_{03})$ ，其中， $t_1$ 由缓动曲线 $f(y-y_0)$ 给出。因此，一个点总共会计算3次插值。

这样以后，就可以在每一个正方形单元都进行计算，对每一个点得到其柏林噪声（代表着它们的高度值），于是得到了上图中连续曲面的效果，下面附上计算过程的动图：

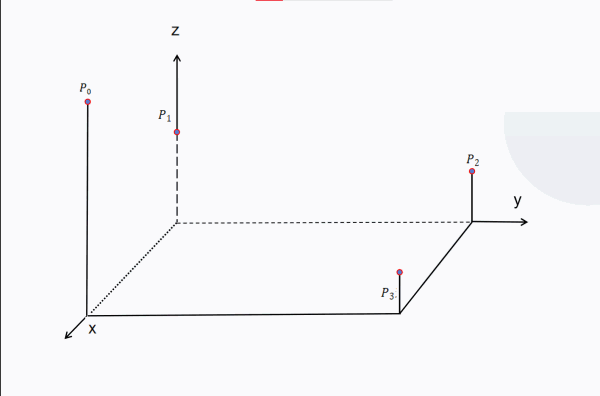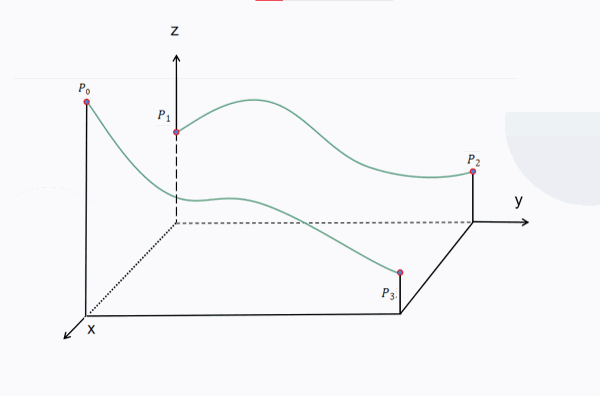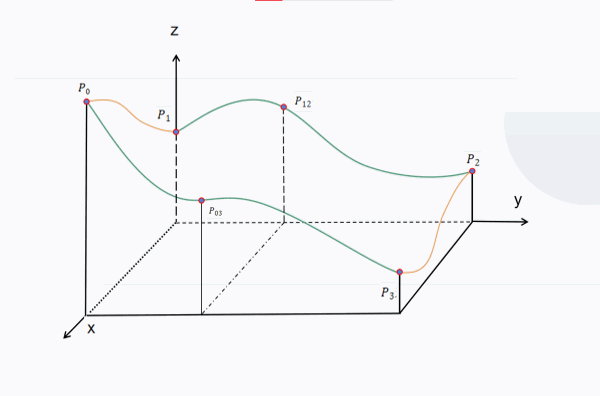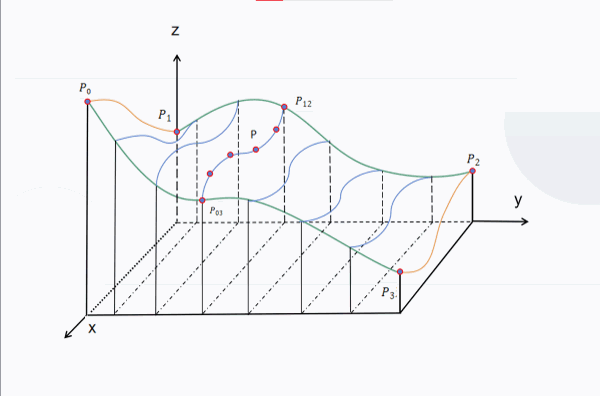
MC中一个正方形单元是一个区块(chunk)，一个区块边长为16个方块，所以在计算时得把结果除以16。这是我的随机地形生成结果:

遗留问题

二维的概念不易理解，我在实现算法时遇到了很多问题。例如：

在二维柏林噪声的动图演示中，它首先计算了y轴方向的 $P_0和P_3$ ， $P_1和P_2$ 。但是如果先计算x轴方向的 $P_0和P_1$ , $P_2和P_3$ ,再用 $P_{01}和P_{23}$ 进行插值，两个方式得出的结果是一样的吗，如何证明？我认为结果一样，但是找不到优雅的证法；
在一个正方形晶格内部，曲面方程 $s (x, y)$ 肯定是关于x,y的幂函数，因而对于曲面内的任意一点，必然处处连续可微，但是在正方形边界的情况呢？有连续性吗？有可微性吗？

期待大家的答案！

三维柏林噪声

一维进行了1次插值，二维进行了3 ( $KaTeX parse error: Undefined control sequence: \* at position 3: =2\̲*̲1+1$ )次插值，那么以此类推，三维应该进行 $KaTeX parse error: Undefined control sequence: \* at position 3: (2\̲*̲3+1)=7$ 次插值。步骤类似，下面就不一一列出，为大家附一张计算图：

效果展示

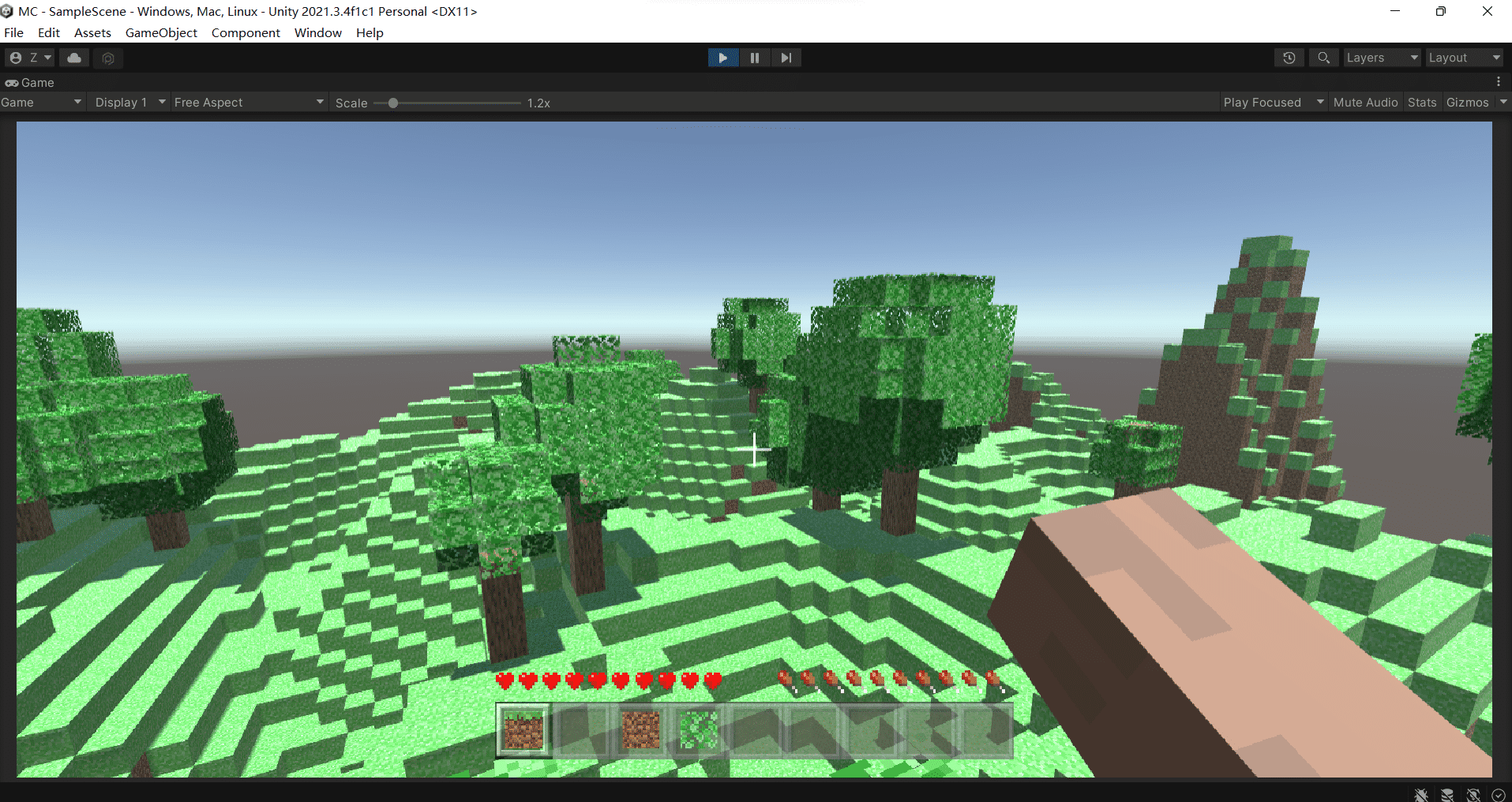
Unity中自带有二维柏林噪声函数：Mathf.PerlinNoise(float x,float y) 输入参数为浮点坐标 $(x, y)$ ，返回二维柏林噪声得出的结果，该结果绝大多数情况范围是[0,1]。我自己写的柏林噪声函数算法偏慢，所以我直接使用了Unity自带的柏林噪声函数，并且加入了伪随机生成树木的算法，看起来还是比较像原版MC的 😃

然后加入了矿洞生成算法，因为Unity没有提供三维的柏林噪声函数，所以我想了个歪招：对于每个方块 $(x, y, z)$ ，计算三次二维柏林噪声：

float result = Mathf.PerlinNoise(x,y) + Mathf.PerlinNoise(y,z) + Mathf.PerlinNoise(z,x);

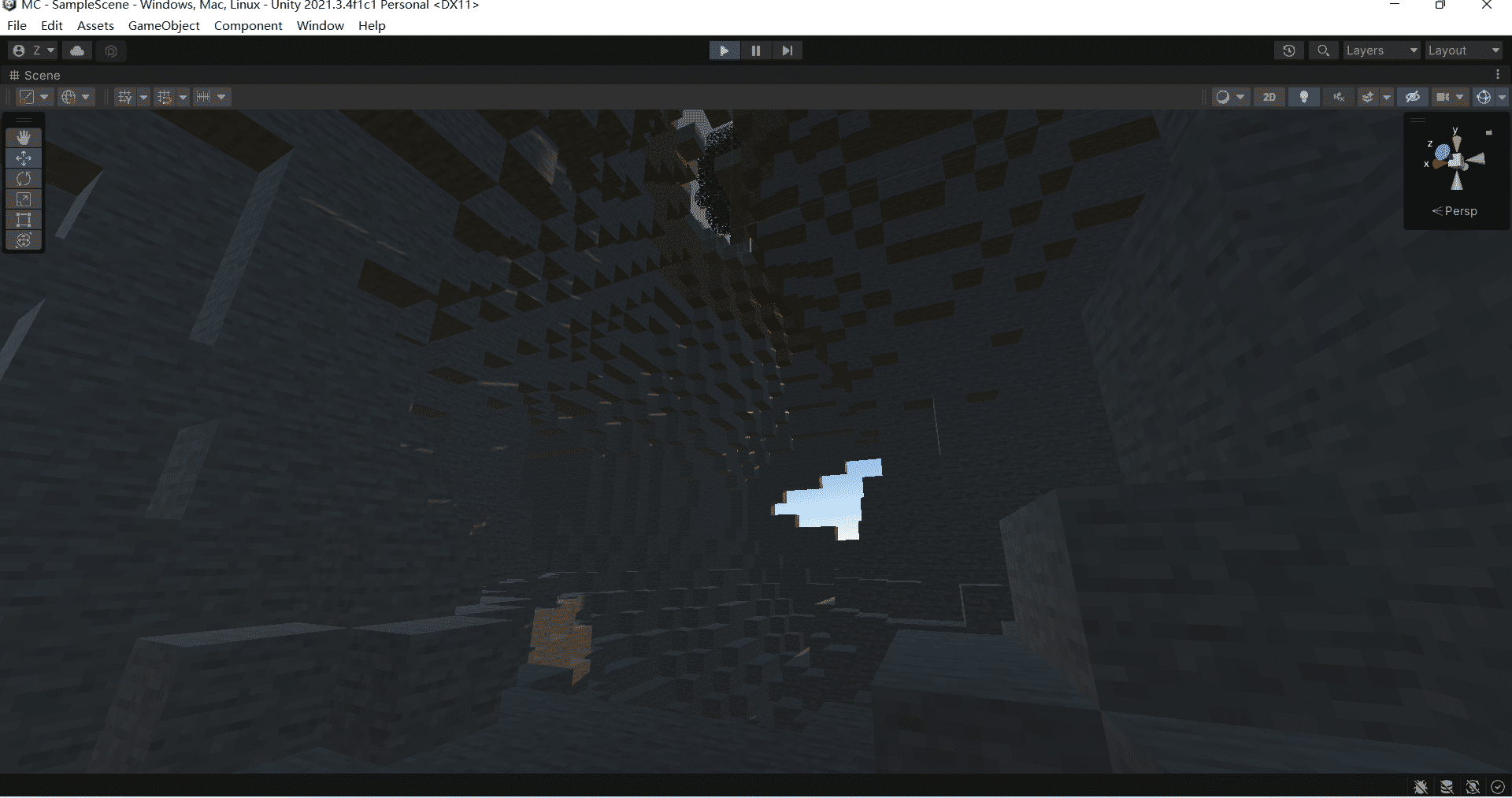
根据result的结果判定是否生成矿洞，以下是矿洞的一部分：

全貌长这样，随机地图会随着玩家位置更新

参考

[1] https://zhuanlan.zhihu.com/p/206271895

[2] 理解柏林噪声_Liukairui的博客-CSDN博客_柏林噪声

[3] 关于柏林噪声，你可这样理解 - 编程开发 - Minecraft(我的世界)中文论坛 -

[4] 柏林噪声（PerlinNoise） - 百度文库