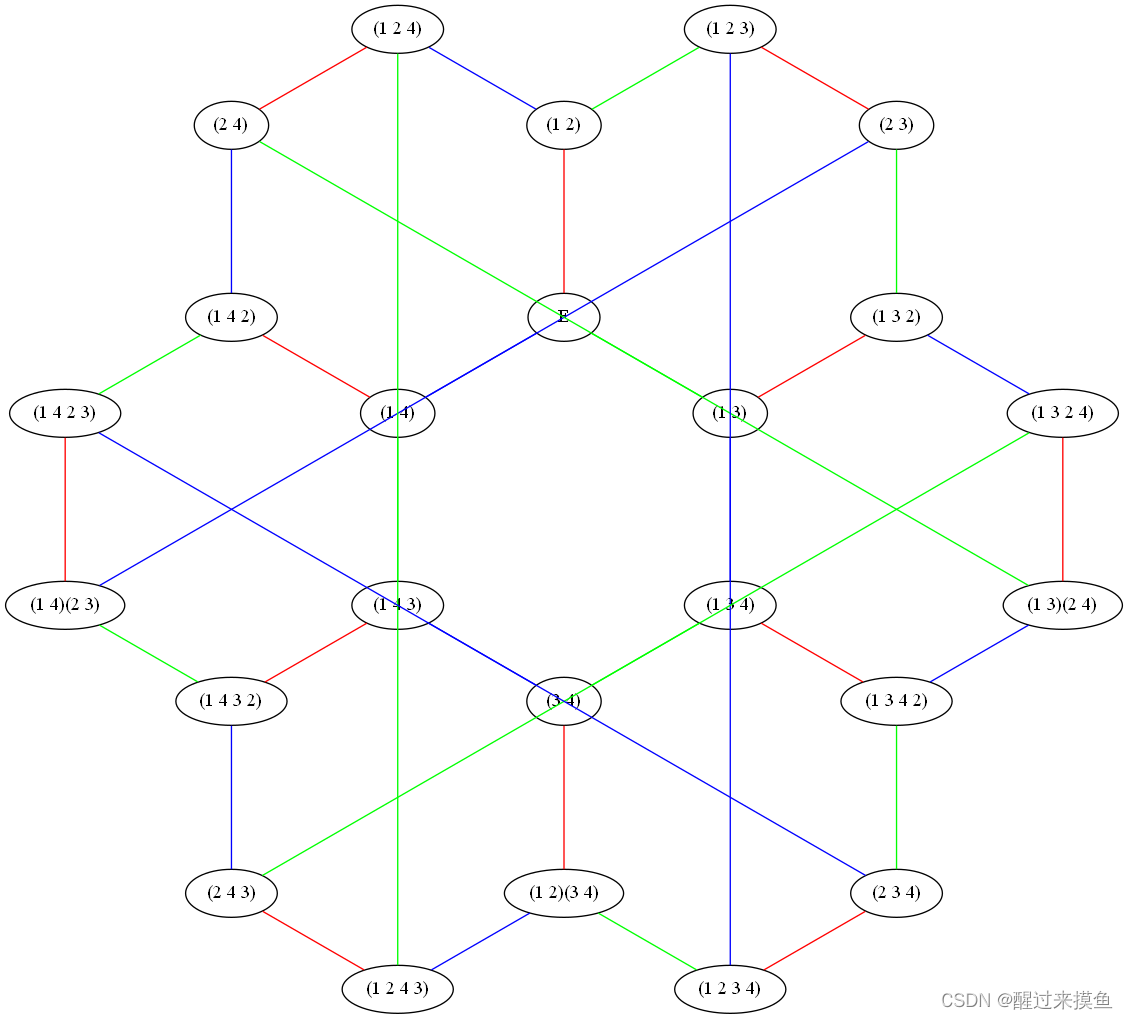
对称群是由N个元素的所有置换组成的群。一个置换对应于一个排列。前面讲到了的正三角形的symmetry group和二面体群$D_3$都实际上是对称群。对称群的符号是S，比如$S_3$就有六个元素，事实上它同构于$D_3$。所以再讨论$S_3$就没有什么意思了。所以来看$S_4$吧。因为是四元素的置换，4元素的所有排列是$4!=24$种。凯莱图有几种画法。
  最简单的用(1 2)、(1 3)和(1 4)作为生成元，凯莱图如下：

  图中虽然线条重叠，但是重叠的颜色是一样的，哈哈，数学是不是特别美呢？这不是巧合，可以证明，无论怎么变换生成元和元素位置，只要按上述画法，重叠的线条颜色一定一样。但是这种画法，重叠得并不好看，在三维时间找不到对应的空间构型。我们换个生成元，比如用(1 2)和（1 2 3 4）这两个置换。

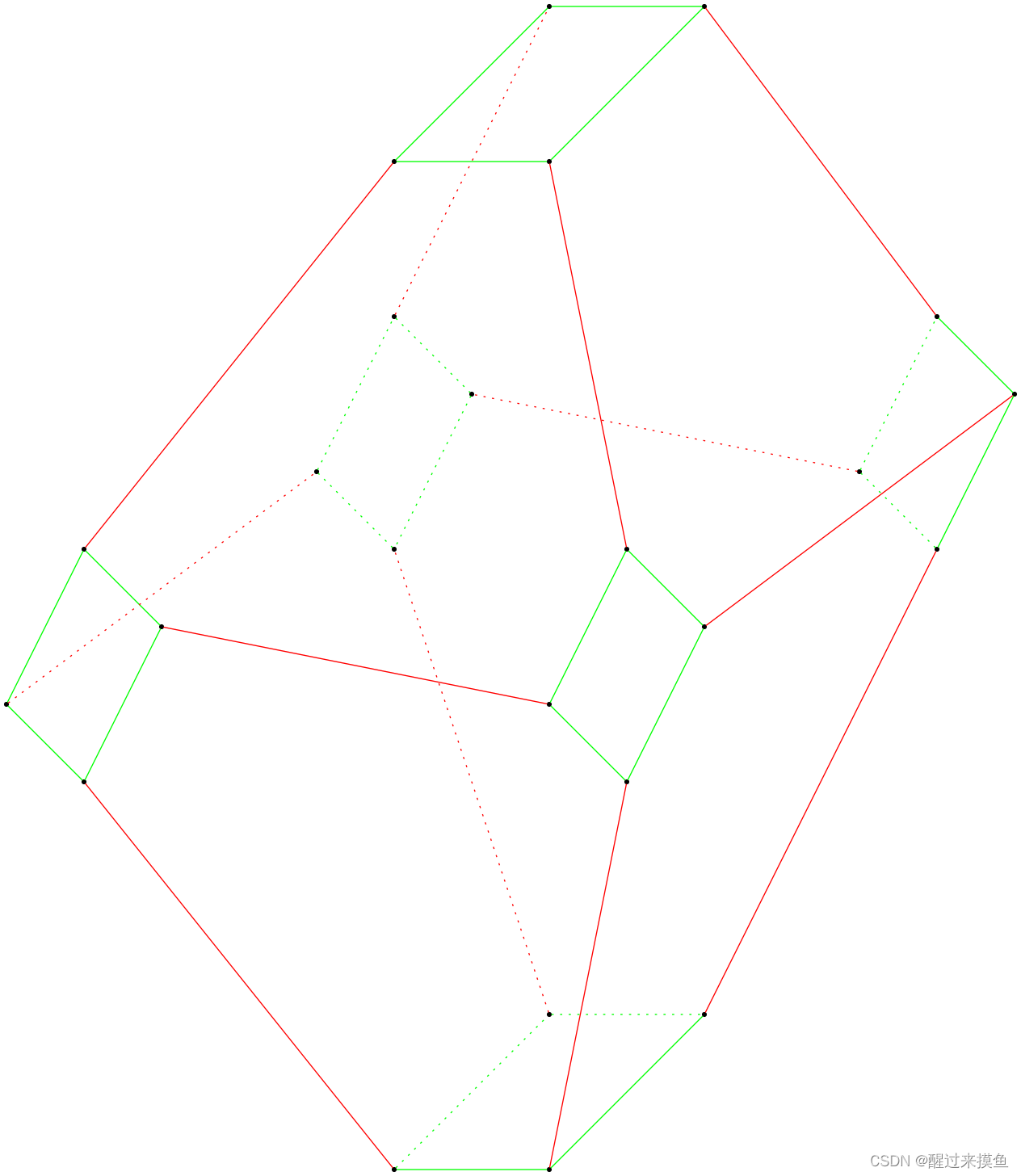
  将群里的元素简化为点，再看看效果：

  这样就非常清晰了，原来是一个切了角的正八面体啊。为了避免线段的重叠和简化模型，一般使用两个生成元来绘制对称群的凯莱图。对称群的子群叫置换群。因为$S_4$的乘法表太复杂，我这里就不写乘法表出来了。