机器学习之决策树模型

一、分类决策树定义

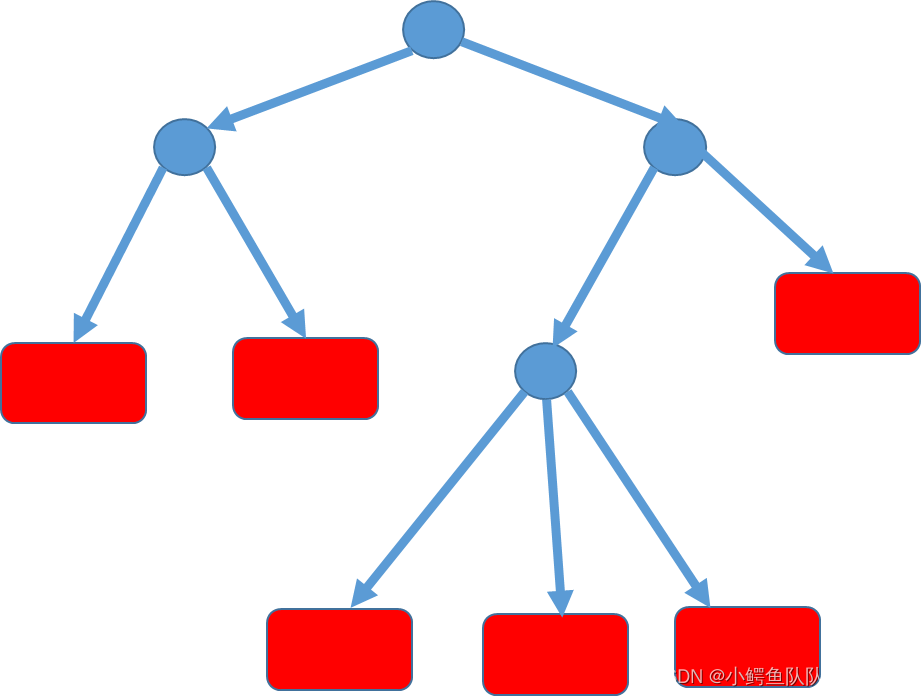
决策树（decision tree）是一种基本分类与回归方法。分类决策树模型是一种描述对实例进行分类的树状结构。决策树有节点和有向边组成。节点分为内部节点和叶节点。内部节点表示一个特征或属性(如图圆圈所示)，叶节点表示一个类（如图方框所示）。

二、决策树学习

决策树思想来源于Quinlan1986年提出的ID3算法和1993年提出的C4.5算法，以及Breiman等人提出的CART算法。
该算法构建一种树状模型，通过if-then规则，或者定义在特征空间与类空间上的条件概率分布实现决策判断。决策树的三个主要步骤：特征划分选择、决策树生成和决策树修剪。
决策树学习目标，是根据给定的训练集构建一个决策树模型。数据集： $D={(x_1,y_1),(x_2,y_2)....,(x_n,y_n)}$

2.1 样本决策划分策略

（1）信息熵定义

热力学中热熵是表示分子状态混乱程度的物理量。1948年，香农提出信息熵（entropy）概念，表示信息源的不确定性，解决了信息量化度量问题。
在决策树划分中，运用信息熵进行分类纯度的表示，从而作为分类判决的一个准则。对任意随机变量 $X$ ,信息熵定义如下：
$Ent(D)=-\displaystyle\sum_{k=1}^{|y|}p_{k}log_2p_{k}$
$E n t (D)$ 越小，表明 $D$ 纯度越高，同类度越高。

（2）判决策略

不难理解，一次判决从而减少的信息熵越多，则这个判决效果该是越好。根据此思想，人们提出了通过评判前后信息熵的差（也称信息增益）的大小选择划分点的判决策略。除了信息增益，之外，还有增益率、基尼指数等作判决策略。
1）信息增益 对于样本离散属性 $a$ 对样本集进行划分，则划分前信息熵和划分后信息熵差值称为信息增益。
$\operatorname{Gain}(D, a)=Ent(D)-Ent(D|a)=Ent(D)-\displaystyle\sum_{v=1}^V\frac{|D^v|}{|D|})Ent(D^v)$
其中，D^v是所有的a属性在第 $v$ 个分支节点上取值为 $a^v$ 的样本数。分支节点的权值为 $\frac{|D^v|}{|D|}$
该准则原理简洁。但是如果某属性分类越多，也就是说越细密，自然信息增益会越大，从而出现该算法偏好特征多分类的特质。为了减少这一偏好带来的不利影响，可以采用单位熵的信息增益作为判决指标。
ID3算法核心就是在决策树各个节点上使用如上所述信息增益准则选择特征，递归都贱决策树。
2）增益率 每一个单的熵所产生的信息增益。计算公式为：
$\operatorname{Gain-ratio}(D, a)=\frac{Gain(D,a)}{IV(a)}$
其中， $IV(a)=-\displaystyle\sum_{v=1}^V\frac{|D^v|}{|D|}log_2 \frac{|D^v|}{|D|}$
这种通过增益率来选择特征方法称为C4.5。通过实例分析，可以看出，该方法出现了偏向于选择取值较少的特征。因此，在实际场景中，一般不会直接把所有特征按照信息增益比从高到低排序，选择信息增益比最大特征作为优选的特质。实际场景中，可以将ID3和C4.5算法结合起来，先按照信息增益排序，选出高于一定阈值的特征。将信息增益超过平均水平的这些特征计算增益率，再从这些特征中选择信息增益比最高的特征出来。
3）基尼指数
不同于信息增益和增益率，意大利统计和社会学家Corrado Gini在1922年提出了基尼指数 $G ini (P)$ ，用来表示一个样本集合中随机选中的样本被分错的概率。设数据集D的某个特征a有 $v$ 个不同取值，第 $i$ 个取值概率为 $P_i$ 。数据集D的纯度用基尼指数定义为：
$Gini(D)=\displaystyle\sum_{i=1}^Vp_i(1-p_i)$
属性a的基尼指数定义为：
$Gini-index(D,a)=\displaystyle\sum_{i=1}^V\frac{|D^v|}{|D|}Gini(D^v)$

从定义可以看出，基尼指数越小，信息纯度越高。基尼系数在简化模型计算的同时保留了信息熵特性，被用来作为反映信息纯度而运用于CART（classfication and regression tree）中离散型输出的分类树预测中：将基尼指数最小的属性作为优先划分属性。对于连续性输出的预测模型，采用最小二乘法作为特征选择指标。

2.2 决策中的问题处理

（1）剪枝处理-

为预防决策树学习算法的“过拟合”，并优化算法，出现了“预剪枝”和“后剪枝”两种策略。

（2）连续值处理

针对数据集某一特征属于连续值的问题，传统离散化技术不能分类问题，因此，最简答策略是采用二分法（bi-partition）对连续属性进行处理，也是C4.5运用的机制。

（3）缺失值处理

针对不完整样本信息，通过赋予权值方法实现信息增益准则的推广应用，从而最大程度进行了样本信息的运用。

（4）样本多个属性联合处理

针对复杂的分类边界，若单纯采用针对一个属性的平行于坐标轴的分类方法，则需要多段分类。为了减少多段分类和大量的属性测试，采用对多个属性的线性组合后进行测试，从而建立一个适合的线性分类器，有效进行决策判别。

三、编程实现

1针对《机器学习》西瓜书中表4.3中的数据，基于信息熵进行划分选择的决策树方法生成一颗决策树。

import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

#加载数据集
df_watermelon=pd.read_csv("D:/ML/3data/watermelon3allenglish.csv")

 #将字符变量转换为数字
 #取字符串的数组
 cols = ['color','root','voice','textrue','umb','feeling']
#映射字典
col_dicts = {}
col_dicts = {
	    'color':{
   			 'green':0,
 			  'black':1,
 			  'white':2
    
},
'root':{ 
    'curl':0,
    'curlbit':1,
    'hard':2
    
},
'voice':{   
    'turbid':0,
    'depressing':1,
    'crisp':2
    
},
'textrue':{
    'clear':0,
    'slightlydim':1,
    'dim':2
    
},
'umb':{
    'sunken':0,
    'sunkenbit':1,
    'flat':2
   
},
'feeling':{
    'smooth':0,
    'stick':1
   
}

}

for col in cols:
		df_watermelon[col] = df_watermelon[col].map(lambda x:x.strip())
		df_watermelon[col] = df_watermelon[col].map(col_dicts[col])

#划分数据集：40%测试集，60%训练集

X=df_watermelon.drop(['target'],axis=1)
y=df_watermelon.target.values
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size=0.4, random_state=1)

#运用信息熵模型进行决策树构建
 df = DecisionTreeClassifier(criterion='entropy')
df= df.fit(X_train, y_train)  # 拟合
# 使用plot_tree函数绘制决策树
feature_names = ['color','root','voice','textrue','umb','feeling','density','ratio']
class_names = ['good', 'sorry']
plt.figure(figsize = (10,8))
tree.plot_tree(df,feature_names = feature_names,  
           class_names=class_names,
           filled = True)
plot_tree(df,filled=True)

predict_y = df.predict(X_test)
print("预测样本特数据集：\n", X_test)
print("对测试集样本的预测结果：\n", predict_y)
predict_y1 = df.predict_proba(X_test)
print("预测样本为某个标签的概率：\n", predict_y1)
print("准确率：",df.score(X_test,y_test))
predict_y = df.predict([[1,1,0,1,1,0,0.6,0.1]])  
print("新样本预测结果：", predict_y)

运行结果：

        预测样本特数据集：
 color  root  voice  textrue  umb  feeling  density  ratio
 3       0     0      1        0    0        0    0.608  0.318
 13      2     1      1        0    0        0    0.657  0.198
 7       1     1      0        0    1        0    0.437  0.211
 2       1     0      0        0    0        0    0.634  0.264
 6       1     1      0        1    1        1    0.481  0.149
 10      2     2      2        2    2        0    0.245  0.057
 4       2     0      0        0    0        0    0.556  0.215
对测试集样本的预测结果：
 [1 0 1 1 0 0 1]
预测样本为某个标签的概率：
[[0. 1.] [1. 0.] [0. 1.] [0. 1.] [1. 0.] [1. 0.] [0. 1.]]
准确率： 0.9411764705882353
新样本预测结果： [0]
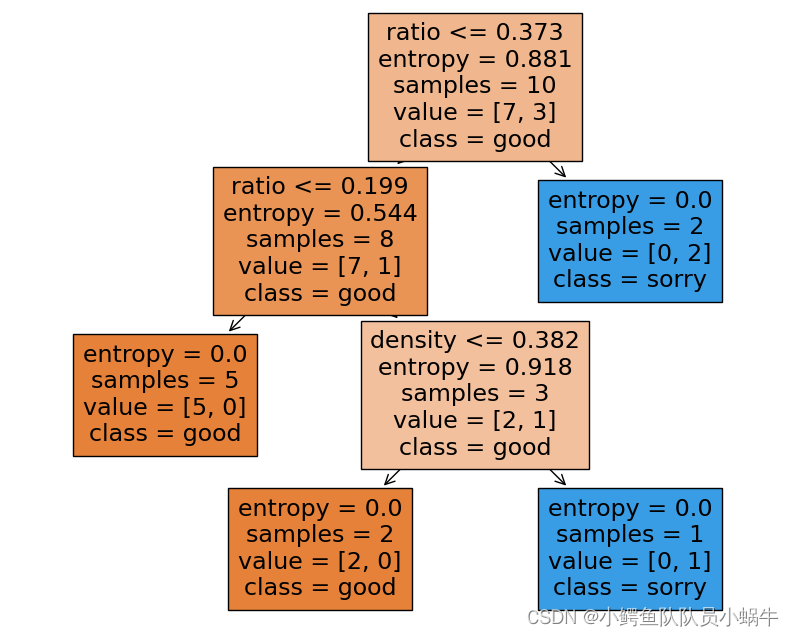
 决策树模型如下：

====

2针对《机器学习》西瓜书中表4.3中的数据，基于基尼指数进行划分选择的决策树方法生成一颗决策树。

  将上面程序中
  df = DecisionTreeClassifier(criterion='entropy')
  更改为：
  df = DecisionTreeClassifier(criterion='gini')

输出结果为：

 预测样本特数据集：
 color  root  voice  textrue  umb  feeling  density  ratio
 3       0     0      1        0    0        0    0.608  0.318
 13      2     1      1        0    0        0    0.657  0.198
 7       1     1      0        0    1        0    0.437  0.211
 2       1     0      0        0    0        0    0.634  0.264
 6       1     1      0        1    1        1    0.481  0.149
 10      2     2      2        2    2        0    0.245  0.057
 4       2     0      0        0    0        0    0.556  0.215
 对测试集样本的预测结果：
  [0 0 1 0 0 0 1]
预测样本为某个标签的概率：
 [[1. 0.] [1. 0.] [0. 1.] [1. 0.] [1. 0.] [1. 0.] [0. 1.]]
 准确率： 0.8235294117647058
 新样本预测结果： [0]