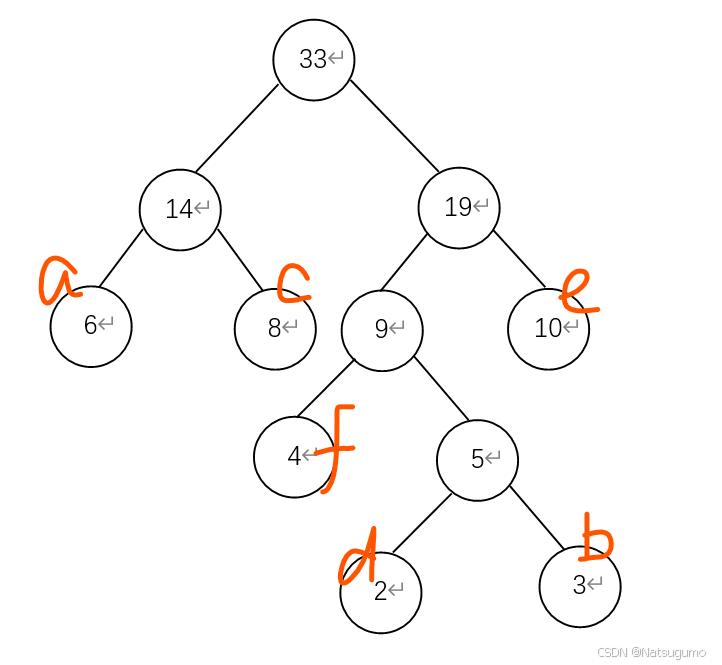
【题目】已知字符集{ a, b, c, d, e, f },若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 },则对应字符集中各字符的哈夫曼编码可能为( )
A. 00, 1011, 01, 1010, 11, 100
B. 11, 100, 110, 000, 0010, 01
C. 10, 1011, 11, 0011, 00, 010
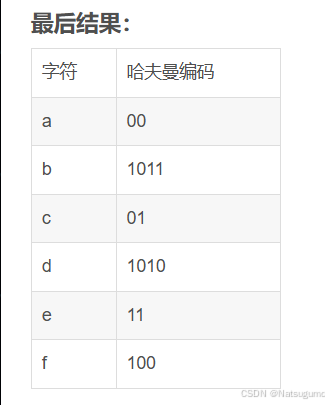
D. 0011, 10, 11, 0010, 01, 000 答案:A
解:
我们首先来根据已知字符集和出现次数构建哈夫曼树(最优二叉树),
出现次数,是为了将短的二进制码分配给频率高的字母,以达到缩短二进制码长度的目的。
如何构建?
1、构建棵只有根节点的二叉树构成森林,根节点的值为n个字母与权值,n个不同的字母,对
应n个权值。这里我们是5个字母{ a, b, c, d, e, f },对应权值{ 6, 3, 8, 2, 10, 4 }。
2、在森林里选出两颗根节点值最小的树进行合并,生成一颗新树,根节点值为两颗树根节点
权值之和,且让两棵树作为新树的左右子树。这两棵树就从森林删除了,新树加入森林。
(1)这里我们就是把这6个字符当做6个叶子结点,把字符出现次数当做结点的权重,以此来
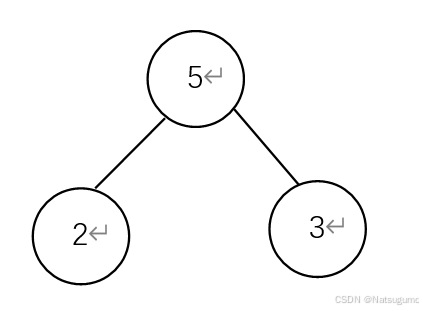
生成一颗哈夫曼树。先找出两个最小的值,2和3。根据小左右大放进树中。
根节点为两树权值之和:2+3=5 。
3、重复2的操作,直到森林只剩一棵树为止,该树即为哈夫曼树。
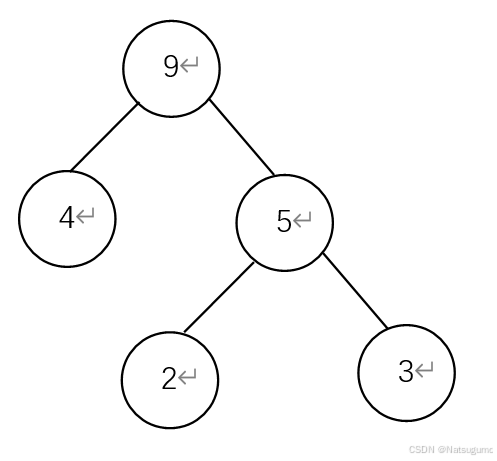
(2)这里我们继续选出两个最小的值,4和6。但我们上一步生成的新树已经加入了森林,
所以是{6,5,8,10,4},5是上一步的根节点,所以这里是4和5。
还是小左右大,根节点为两树权值之和:4+5=9 。
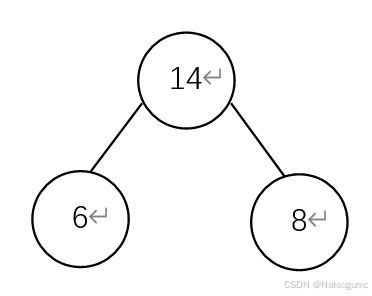
(3)重复,{6,9,8,10},剩余的取两个最小的,6和8。
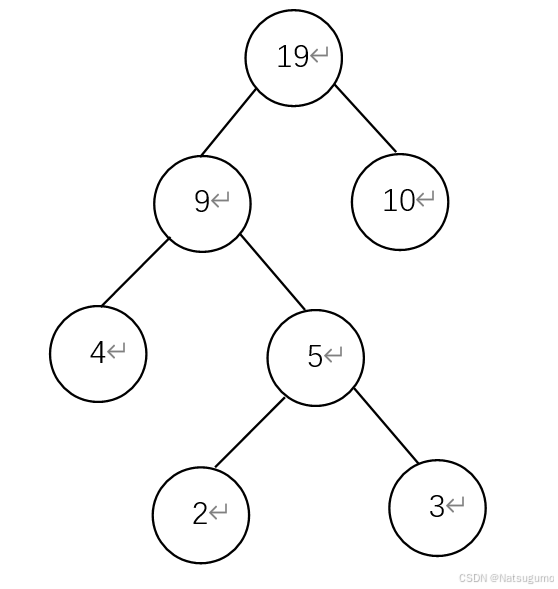
(4)重复,{9,14,10},剩余取两最小,9和10。
(5)最后剩{14,19},再把最后这两一组合。小左右大
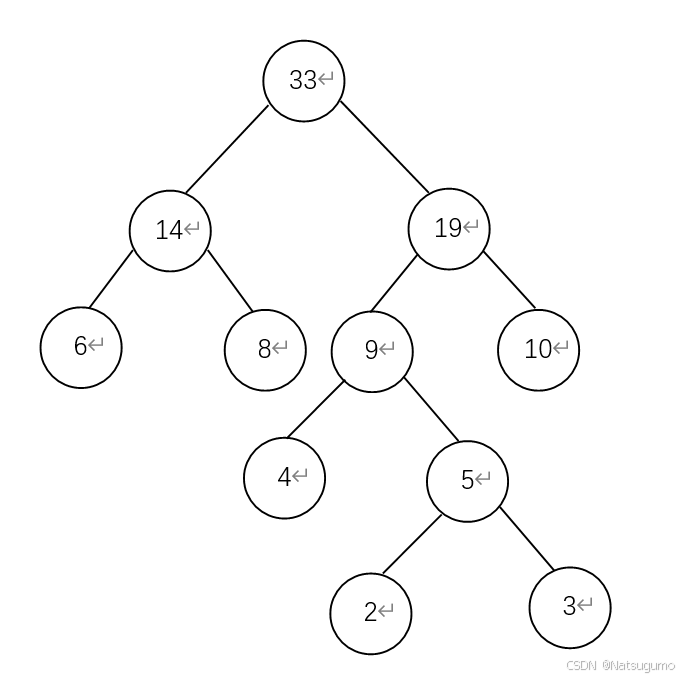
(6)组合完哈夫曼树后,我们将对应的字符填上去。
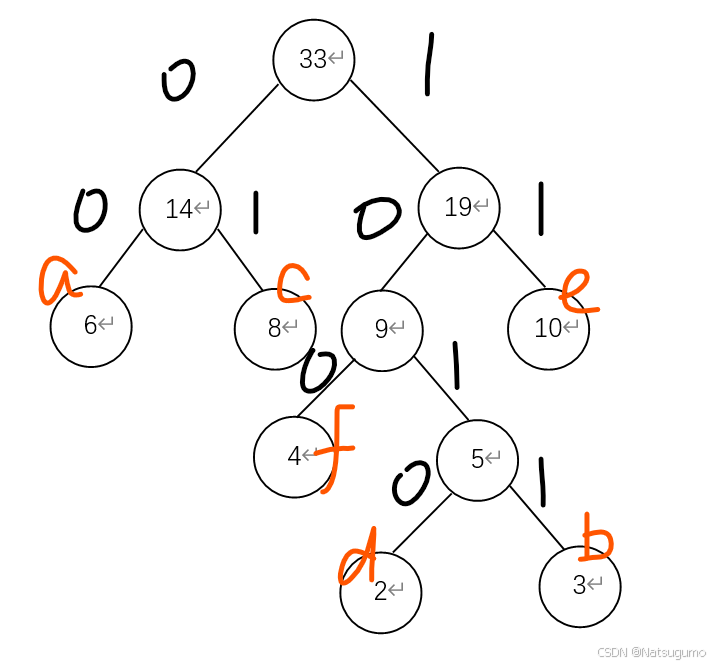
(7)最后我们要对各个字母进行编码,编码原则是,从哈夫曼树的根节点开始,进入左子树
则编码号加0,进入右子树则编码号加1,就可以得到对应字母的二进制编码。就是左0右1。
哈夫曼树通常以二叉树的形式出现,所以也称最优二叉树,是一类带权路径长度最短的树。
哈夫曼编码,又称为霍夫曼编码,它是现代压缩算法的基础。
哈夫曼编码(Huffman Coding)
哈夫曼树的应用很广,哈夫曼编码就是其在电讯通信中的应用之一。
广泛地用于数据文件压缩的十分有效的编码方法。
计算机二进制有两种状态0和1,
通常用二进制编码来表示字母或其他字符,并用这样的编码来表示字符序列。
———————————————————————
总忘记这些冗杂琐碎的知识点,做题的时候想不起来,搜索的时候又半天看不懂,其实主要是不简洁明了,看不进去,就顺手记录一下,顺便梳理梳理思绪。
目前我们不必把我每个知识点搞的那么细致,软考需要,得会做类似的题,主要是要记住做题思路。