文章目录
1.788. 旋转数字
我们称一个数 X 为好数, 如果它的每位数字逐个地被旋转 180 度后,我们仍可以得到一个有效的,且和 X 不同的数。要求每位数字都要被旋转。
如果一个数的每位数字被旋转以后仍然还是一个数字, 则这个数是有效的。0, 1, 和 8 被旋转后仍然是它们自己;2 和 5 可以互相旋转成对方(在这种情况下,它们以不同的方向旋转,换句话说,2 和 5 互为镜像);6 和 9 同理,除了这些以外其他的数字旋转以后都不再是有效的数字。
现在我们有一个正整数 N, 计算从 1 到 N 中有多少个数 X 是好数?
示例:
输入: 10
输出: 4
解释:
在[1, 10]中有四个好数: 2, 5, 6, 9。
注意 1 和 10 不是好数, 因为他们在旋转之后不变。
既然这次主题是模拟,就直接按照题目意思硬算了(当然可以用dp优化)
class Solution {
public:
bool check(int num){
bool flag=false;
while(num){
if(num%10==3||num%10==4||num%10==7){
return false;
}
if(num%10==2||num%10==5||num%10==6||num%10==9){
flag=true;
}
num/=10;
}
return flag;
}
int rotatedDigits(int n) {
if(n<2){
return 0;
}
int ans=1;
for(int i=3;i<=n;i++){
ans+=check(i);
}
return ans;
}
};
2.38. 外观数列
给定一个正整数 n ,输出外观数列的第 n 项。
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。
你可以将其视作是由递归公式定义的数字字符串序列:
countAndSay(1) = “1”
countAndSay(n) 是对 countAndSay(n-1) 的描述,然后转换成另一个数字字符串。
前五项如下:
111211211111221第一项是数字 1
描述前一项,这个数是 1 即 “ 一 个 1 ”,记作 “11”
描述前一项,这个数是 11 即 “ 二 个 1 ” ,记作 “21”
描述前一项,这个数是 21 即 “ 一 个 2 + 一 个 1 ” ,记作 “1211”
描述前一项,这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ,记作 “111221”
要 描述 一个数字字符串,首先要将字符串分割为 最小 数量的组,每个组都由连续的最多 相同字符 组成。然后对于每个组,先描述字符的数量,然后描述字符,形成一个描述组。要将描述转换为数字字符串,先将每组中的字符数量用数字替换,再将所有描述组连接起来。
示例 1:
输入:n = 1
输出:“1”
解释:这是一个基本样例。
示例 2:
输入:n = 4
输出:“1211”
解释:
countAndSay(1) = “1”
countAndSay(2) = 读 “1” = 一 个 1 = “11”
countAndSay(3) = 读 “11” = 二 个 1 = “21”
countAndSay(4) = 读 “21” = 一 个 2 + 一 个 1 = “12” + “11” = “1211”
提示:
1 <= n <= 30
这道题刚开始读的时候我是十分不理解,看了几遍示例之后才懂,我们把字符串两个两个的读,比如s[2]=11,他就代表前一个数字是一个一(1),s[3]=21前一个数字是两个一(11),s[4]=1211,分为12 ,11代表前一个数字是一个2和1个1(21),那么找到了规律之后就简单了,n最大仅为30模拟即可.
class Solution {
public:
string getans(int count){
string ans="";
while(count){
ans.push_back((count%10)+'0');
count/=10;
}
reverse(ans.begin(),ans.end());
return ans;
}
string dp(string ans){
int start=0;//开始读的位置
string s="";
for(int i=1;i<=ans.size();i++){
//两个两个的读可以算出相应的下标关系
if(i==ans.size()||ans[i]!=ans[i-1]){
//如过读到了前一个字符串的末尾或者遇到了不同的数字开始构造下个字符串
int count=i-start;//统计个数
s+=getans(count)+ans[i-1];
start=i;
}
}
return s;
}
string countAndSay(int n) {
string ans="1";//基本情况
while(--n){
ans=dp(ans);
}
return ans;
}
};
3.2075. 解码斜向换位密码
字符串 originalText 使用 斜向换位密码 ,经由 行数固定 为 rows 的矩阵辅助,加密得到一个字符串 encodedText 。
originalText 先按从左上到右下的方式放置到矩阵中。
先填充蓝色单元格,接着是红色单元格,然后是黄色单元格,以此类推,直到到达 originalText 末尾。箭头指示顺序即为单元格填充顺序。所有空单元格用 ’ ’ 进行填充。矩阵的列数需满足:用 originalText 填充之后,最右侧列 不为空 。
接着按行将字符附加到矩阵中,构造 encodedText 。
先把蓝色单元格中的字符附加到 encodedText 中,接着是红色单元格,最后是黄色单元格。箭头指示单元格访问顺序。
例如,如果 originalText = “cipher” 且 rows = 3 ,那么我们可以按下述方法将其编码:
蓝色箭头标识 originalText 是如何放入矩阵中的,红色箭头标识形成 encodedText 的顺序。在上述例子中,encodedText = “ch ie pr” 。
给你编码后的字符串 encodedText 和矩阵的行数 rows ,返回源字符串 originalText 。
注意:originalText 不 含任何尾随空格 ’ ’ 。生成的测试用例满足 仅存在一个 可能的 originalText 。
示例 1:
输入:encodedText = “ch ie pr”, rows = 3
输出:“cipher”
解释:此示例与问题描述中的例子相同。
示例 2:
输入:encodedText = “iveo eed l te olc”, rows = 4
输出:“i love leetcode”
解释:上图标识用于编码 originalText 的矩阵。
蓝色箭头展示如何从 encodedText 找到 originalText 。
示例 3:
输入:encodedText = “coding”, rows = 1
输出:“coding”
解释:由于只有 1 行,所以 originalText 和 encodedText 是相同的。
示例 4:
输入:encodedText = " b ac", rows = 2
输出:" abc"
解释:originalText 不能含尾随空格,但它可能会有一个或者多个前置空格。
提示:
0 <= encodedText.length <= 106
encodedText 仅由小写英文字母和 ’ ’ 组成
encodedText 是对某个 不含 尾随空格的 originalText 的一个有效编码
1 <= rows <= 1000
生成的测试用例满足 仅存在一个 可能的 originalText
这道题的关键还是在于计算我们要返回答案的下标关系,如果看出来了的话就十分简单了,其实每次从第0行第i列开始斜着读取。通过列数可以算出相应的行数
class Solution {
public:
string decodeCiphertext(string encodedText, int row) {
vector<string> martix;
int col=encodedText.size()/row;
string ans="";
for(int i=0;i<row;i++){
string tmp="";
for(int j=0;j<col;j++){
tmp.push_back(encodedText[i*col+j]);
}
martix.push_back(tmp);//先将字符串映射到我们的二维数组中
}
int nowcol=0;
for(nowcol=0;nowcol<col;nowcol++){//从第0列开始
for(int i=0;i<row;i++){//从第0行开始
int _col=nowcol+i;//现在读取的列数
if(_col>=col) break;//如果越界就退出
ans.push_back(martix[i][_col]);
}
}
while(ans.back()==' '){
ans.pop_back();//删去末尾的空格如果有的话
}
return ans;
}
};
4.2232. 向表达式添加括号后的最小结果
给你一个下标从 0 开始的字符串 expression ,格式为 “+” ,其中 和 表示正整数。
请你向 expression 中添加一对括号,使得在添加之后, expression 仍然是一个有效的数学表达式,并且计算后可以得到 最小 可能值。左括号 必须 添加在 ‘+’ 的左侧,而右括号必须添加在 ‘+’ 的右侧。
返回添加一对括号后形成的表达式 expression ,且满足 expression 计算得到 最小 可能值。如果存在多个答案都能产生相同结果,返回任意一个答案。
生成的输入满足:expression 的原始值和添加满足要求的任一对括号之后 expression 的值,都符合 32-bit 带符号整数范围。
示例 1:
输入:expression = “247+38”
输出:“2(47+38)”
解释:表达式计算得到 2 * (47 + 38) = 2 * 85 = 170 。
注意 “2(4)7+38” 不是有效的结果,因为右括号必须添加在 ‘+’ 的右侧。
可以证明 170 是最小可能值。
示例 2:
输入:expression = “12+34”
输出:“1(2+3)4”
解释:表达式计算得到 1 * (2 + 3) * 4 = 1 * 5 * 4 = 20 。
示例 3:
输入:expression = “999+999”
输出:“(999+999)”
解释:表达式计算得到 999 + 999 = 1998 。
提示:
3 <= expression.length <= 10
expression 仅由数字 ‘1’ 到 ‘9’ 和 ‘+’ 组成
expression 由数字开始和结束
expression 恰好仅含有一个 ‘+’.
expression 的原始值和添加满足要求的任一对括号之后 expression 的值,都符合 32-bit 带符号整数范围
这个题如果模拟来做的话就是枚举所有括号可以添加的情况,以加号,左右括号把原字符串的数字分为四部分:a,b,c,d分别计算每种情况下a*(b+c)*d的结果并取最小,不过代码实现还是有很多细节的。
class Solution {
public:
int getnum(int l,int r,string & s){
int ans=0;
for(int i=l;i<=r;i++){
ans=ans*10+s[i]-'0';
}
return ans;
}
string minimizeResult(string expression) {
int i,j,k,add;
int a,b,c,d;
int min=INT_MAX;
for(i=0;i<expression.size();i++){
if(expression[i]=='+'){
add=i;
break;//找到加号的位置
}
}
string ans="";
for(i=0;i<add;i++){
//i的意义为我们要在i位置左边添加左括号
for(j=add+1;j<expression.size();j++){
//j的意义为我们要在j的右边添加右括号
a=getnum(0,i-1,expression);
//计算左括号之前的数字大小
if(a==0) a=1;
//我们自然而然地想到在i等于0的情况下就越界了
//所以getnum在这种情况下我们认为设置了返回0,这种情况下a=1,下面的d=1同理
b=getnum(i,add-1,expression);
c=getnum(add+1,j,expression);
d=getnum(j+1,expression.size()-1,expression);
if(d==0) d=1;
int num=a*(b+c)*d;
if(min>num){//为ans赋值
min=num;
ans="";
for(k=0;k<i;k++){
ans+=expression[k];
}
ans+="(";
for(k=i;k<=j;k++){
ans+=expression[k];
}
ans+=")";
for(k=j+1;expression[k];k++){
ans+=expression[k];
}
}
}
}
return ans;
}
};
5.59. 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
提示:
1 <= n <= 20
经典题目了,经典的做法是分四个方向来考虑移动的情况,这里的代码有些不同,不过理解了的话其实不难发现就是搜索。
class Solution {
public:
int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};//四个方向右,下,左,上
bool hash[21][21];
vector<vector<int>>ans;
vector<vector<int>> generateMatrix(int n) {
for(int i=0;i<n;i++)
{
vector<int> tmp;
for(int j=0;j<n;j++)
tmp.push_back(0);
ans.push_back(tmp);
}
int x=0,y=0,d=0,id=1;//开始的方向为左
int step=n*n;//要移动的次数
while(step--)
{
ans[x][y]=id++;
hash[x][y]=true;//标记
x+=dir[d][0];
y+=dir[d][1];
if(x==n||x==-1||y==n||y==-1||hash[x][y])
{
x-=dir[d][0];
y-=dir[d][1];
d=(d+1)%4;//越界了就改变方向回退并移动到下个位置
x+=dir[d][0];
y+=dir[d][1];
}
}
return ans;
}
};
6.37. 解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
示例 1:
输入:board = [[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”],[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”],[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”],[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”],[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”],[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”],[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”],[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”],[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出:[[“5”,“3”,“4”,“6”,“7”,“8”,“9”,“1”,“2”],[“6”,“7”,“2”,“1”,“9”,“5”,“3”,“4”,“8”],[“1”,“9”,“8”,“3”,“4”,“2”,“5”,“6”,“7”],[“8”,“5”,“9”,“7”,“6”,“1”,“4”,“2”,“3”],[“4”,“2”,“6”,“8”,“5”,“3”,“7”,“9”,“1”],[“7”,“1”,“3”,“9”,“2”,“4”,“8”,“5”,“6”],[“9”,“6”,“1”,“5”,“3”,“7”,“2”,“8”,“4”],[“2”,“8”,“7”,“4”,“1”,“9”,“6”,“3”,“5”],[“3”,“4”,“5”,“2”,“8”,“6”,“1”,“7”,“9”]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字或者 ‘.’
题目数据 保证 输入数独仅有一个解
这道题的话,就是较为简单的八皇后问题,不同的是少了两个对角线的判断多了对于九宫格的判断。经典的八皇后大家肯定都会了,这里就用位运算来求解了。
class Solution {
public:
int rowmask[10];
int colmask[10];
bool check(int row,int col,vector<vector<char>>& board){
int rowidx=row/3;
int colidx=col/3;//通过行列坐标得到他是第几个九宫格
int hash[10];//标记数字状况
memset(hash,0,sizeof(hash));
for(int i=rowidx*3;i<rowidx*3+3;i++){
for(int j=colidx*3;j<colidx*3+3;j++){
if(board[i][j]=='.'){
continue;
}
if(++hash[board[i][j]-'1']>1){
return false;
}
}
}
return true;
}
bool dfs(int *rowmask,int *colmask,vector<vector<char>> & board,int nowblock,int blocksize,vector<int>& block)
{
if(nowblock==blocksize){
return true;
}//所有的位置都填充过了直接返回
int pos=block[nowblock];
int row=pos/9;
int col=pos%9;//得到要填充位置的坐标
for(int i=1;i<=9;++i){//枚举1-9所有的状况
int num=(1<<(i-1));
if(rowmask[row]&num){
continue;//如果该行上有这个数字continue
}
if(colmask[col]&num){
continue;//如果该列有这个数字continue
}
rowmask[row]^=num;
colmask[col]^=num;
//异或除了他本身的意义外还有一个用法就是非进制加法,当然按位或也可以
board[row][col]=i+'0';//修改这位的信息
if(check(row,col,board)){//检查九宫格合法的话继续下个搜索
if(dfs(rowmask,colmask,board,nowblock+1,blocksize,block)){
return true;
}
}
rowmask[row]^=num;
colmask[col]^=num;
board[row][col]='.';
//九宫格检查不合法或者这种搜索状态不合法回退上个状态
}
return false;
}
void solveSudoku(vector<vector<char>>& board) {
vector<int> block;//标记上“.”的位置这是我们要填充的位置
int blocksize=0;
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j]=='.'){
block.push_back(i*9+j);//转为成一个数字便于获得"."的位置
}
}
}
blocksize=block.size();//我们要填充的个数
for(int i=0;i<9;i++){
rowmask[i]=0;
//每一行的rowmask都先设置成0,然后遍历得到他每行已经有的数字状态下面的colmask同理
for(int j=0;j<9;j++){
rowmask[i]|=(board[i][j]=='.'?0:(1<<(board[i][j]-'1')));
}
}
for(int i=0;i<9;i++){
colmask[i]=0;
for(int j=0;j<9;j++){
colmask[i]|=(board[j][i]=='.'?0:(1<<(board[j][i]-'1')));
}
}
dfs(rowmask,colmask,board,0,blocksize,block);//开始填充
}
};
7.36. 有效的数独
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
注意:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
空白格用 ‘.’ 表示。
示例 1:
输入:board =
[[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”]
,[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”]
,[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”]
,[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”]
,[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”]
,[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”]
,[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”]
,[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”]
,[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出:true
示例 2:
输入:board =
[[“8”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”]
,[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”]
,[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”]
,[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”]
,[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”]
,[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”]
,[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”]
,[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”]
,[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出:false
解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字(1-9)或者 ‘.’
这道题就是上一道题的其中一个判断过程,因为题目要求的就是让我们判断这个状态下的数独是否可以被填充。
class Solution {
public:
int rowmask[10],colmask[10],gongmask[10];
int getgongidx(int i,int j){
return (i/3)*3+j/3;
}
bool isValidSudoku(vector<vector<char>>& board) {
memset(rowmask,0,sizeof(rowmask));
memset(colmask,0,sizeof(colmask));
memset(gongmask,0,sizeof(gongmask));
for(int i=0;i<9;++i){
for(int j=0;j<9;++j){
if(board[i][j]!='.'){
int num=(1<<(board[i][j]-'1'));
if(rowmask[i]&num){
return false;
}
if(colmask[j]&num){
return false;
}
if(gongmask[getgongidx(i,j)]&num){
return false;
}
rowmask[i]|=num;
colmask[j]|=num;
gongmask[getgongidx(i,j)]|=num;
}
}
}
return true;
}
};
8.1222. 可以攻击国王的皇后
在一个 8x8 的棋盘上,放置着若干「黑皇后」和一个「白国王」。
给定一个由整数坐标组成的数组 queens ,表示黑皇后的位置;以及一对坐标 king ,表示白国王的位置,返回所有可以攻击国王的皇后的坐标(任意顺序)。
示例 1:
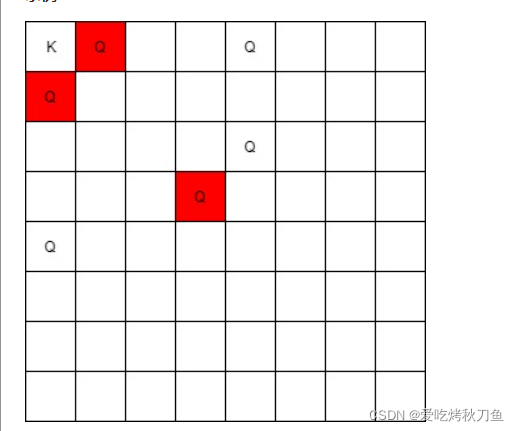
输入:queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
输出:[[0,1],[1,0],[3,3]]
解释:
[0,1] 的皇后可以攻击到国王,因为他们在同一行上。
[1,0] 的皇后可以攻击到国王,因为他们在同一列上。
[3,3] 的皇后可以攻击到国王,因为他们在同一条对角线上。
[0,4] 的皇后无法攻击到国王,因为她被位于 [0,1] 的皇后挡住了。
[4,0] 的皇后无法攻击到国王,因为她被位于 [1,0] 的皇后挡住了。
[2,4] 的皇后无法攻击到国王,因为她和国王不在同一行/列/对角线上。
示例 2:
输入:queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
输出:[[2,2],[3,4],[4,4]]
示例 3:
输入:queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
输出:[[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]
从八个方向搜索看是否有皇后即可。
class Solution {
public:
int dir[8][2]={{-1,-1},{-1,0},{-1,1},{0,1},{0,-1},{1,-1},{1,0},{1,1}};
vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
bool queen[8][8];
memset(queen,false,sizeof(queen));
for(int i=0;i<queens.size();++i){
int x=queens[i][0];
int y=queens[i][1];
queen[x][y]=true;
}
int kingx=king[0];
int kingy=king[1];
vector<vector<int>> ans;
for(int i=0;i<8;++i){
int x=kingx,y=kingy;
while(1){
x+=dir[i][0];
y+=dir[i][1];
if(x<0||y<0||x>=8||y>=8){
break;
}
if(queen[x][y]){
ans.push_back({x,y});
break;
}
}
}
return ans;
}
};
9.657. 机器人能否返回原点
在二维平面上,有一个机器人从原点 (0, 0) 开始。给出它的移动顺序,判断这个机器人在完成移动后是否在 (0, 0) 处结束。
移动顺序由字符串 moves 表示。字符 move[i] 表示其第 i 次移动。机器人的有效动作有 R(右),L(左),U(上)和 D(下)。
如果机器人在完成所有动作后返回原点,则返回 true。否则,返回 false。
注意:机器人“面朝”的方向无关紧要。 “R” 将始终使机器人向右移动一次,“L” 将始终向左移动等。此外,假设每次移动机器人的移动幅度相同。
示例 1:
输入: moves = “UD”
输出: true
解释:机器人向上移动一次,然后向下移动一次。所有动作都具有相同的幅度,因此它最终回到它开始的原点。因此,我们返回 true。
示例 2:
输入: moves = “LL”
输出: false
解释:机器人向左移动两次。它最终位于原点的左侧,距原点有两次 “移动” 的距离。我们返回 false,因为它在移动结束时没有返回原点。
提示:
1 <= moves.length <= 2 * 104
moves 只包含字符 ‘U’, ‘D’, ‘L’ 和 ‘R’
为了能更好的理解下面两题,这里先理解一下这道题。
class Solution {
public:
int dir[4][2]={{0,1},{0,-1},{-1,0},{1,0}};
char direction[5]="RLUD";
int getdirection(char x){
for(int i=0;i<5;i++){
if(direction[i]==x){
return i;
}
}
return -1;
}
bool judgeCircle(string moves) {
int x=0,y=0;
for(int i=0;i<moves.size();++i){
int d=getdirection(moves[i]);
x+=dir[d][0];
y+=dir[d][1];
}
return x==0&&y==0;
}
};
9.874. 模拟行走机器人
机器人在一个无限大小的 XY 网格平面上行走,从点 (0, 0) 处开始出发,面向北方。该机器人可以接收以下三种类型的命令 commands :
-2 :向左转 90 度
-1 :向右转 90 度
1 <= x <= 9 :向前移动 x 个单位长度
在网格上有一些格子被视为障碍物 obstacles 。第 i 个障碍物位于网格点 obstacles[i] = (xi, yi) 。
机器人无法走到障碍物上,它将会停留在障碍物的前一个网格方块上,但仍然可以继续尝试进行该路线的其余部分。
返回从原点到机器人所有经过的路径点(坐标为整数)的最大欧式距离的平方。(即,如果距离为 5 ,则返回 25 )
注意:
北表示 +Y 方向。
东表示 +X 方向。
南表示 -Y 方向。
西表示 -X 方向。
示例 1:
输入:commands = [4,-1,3], obstacles = []
输出:25
距离原点最远的是 (3, 4) ,距离为 32 + 42 = 25
示例 2:
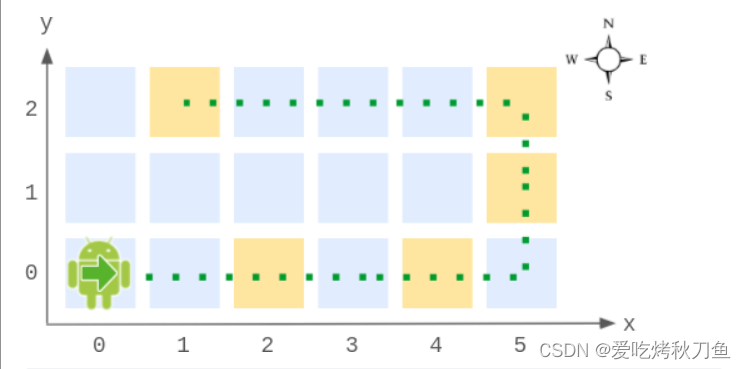
输入:commands = [4,-1,4,-2,4], obstacles = [[2,4]]
输出:65
距离原点最远的是 (1, 8) ,距离为 12 + 82 = 65
提示:
1 <= commands.length <= 10^4
commands[i] is one of the values in the list [-2,-1,1,2,3,4,5,6,7,8,9].
0 <= obstacles.length <= 10^4
-3 * 10^4 <= xi, yi <= 3 * 10^4
答案保证小于 2^31
这也是没什么难度的题,先将障碍物映射到一个哈希表中,这里同样是二维转一维,接着就是开始行走并不断比较,当遇到障碍物的时候注意要退回并continue。同时因为答案保证了不超过int的范围所以在比较的时候我们可以放心的用坐标来计算。
class Solution {
public:
int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
unordered_map< unsigned int,bool> hasobstacl;
unsigned int getBlockCode(int x,int y){
return (unsigned int)(x + 30001) * 60002 + y;
}
bool hasBlock(int x,int y){
unsigned int code = getBlockCode(x, y);
return hasobstacl.find(code)!=hasobstacl.end();
}
void addblock(vector<int>& block){
int x=block[0];
int y=block[1];
unsigned int code = getBlockCode(x, y);
hasobstacl[code]=true;
}
int robotSim(vector<int>& commands, vector<vector<int>>& obstacles) {
hasobstacl.clear();
for(int i=0;i<obstacles.size();++i){
addblock(obstacles[i]);
}
int ans=0;
int d=0;
int x,y;
x=y=0;
for(int i=0;i<commands.size();++i){
if(commands[i]==-1){
d=(d+1)%4;
}else if(commands[i]==-2){
d=(d+3)%4;
}else {
int step=commands[i];
while(step){
x+=dir[d][0];
y+=dir[d][1];
--step;
if(hasBlock(x,y)){
x-=dir[d][0];
y-=dir[d][1];
continue;
}
ans=max(ans,x*x+y*y);
}
}
}
return ans;
}
};
10.2069. 模拟行走机器人 II
给你一个在 XY 平面上的 width x height 的网格图,左下角 的格子为 (0, 0) ,右上角 的格子为 (width - 1, height - 1) 。网格图中相邻格子为四个基本方向之一(“North”,“East”,“South” 和 “West”)。一个机器人 初始 在格子 (0, 0) ,方向为 “East” 。
机器人可以根据指令移动指定的 步数 。每一步,它可以执行以下操作。
沿着当前方向尝试 往前一步 。
如果机器人下一步将到达的格子 超出了边界 ,机器人会 逆时针 转 90 度,然后再尝试往前一步。
如果机器人完成了指令要求的移动步数,它将停止移动并等待下一个指令。
请你实现 Robot 类:
Robot(int width, int height) 初始化一个 width x height 的网格图,机器人初始在 (0, 0) ,方向朝 “East” 。
void move(int num) 给机器人下达前进 num 步的指令。
int[] getPos() 返回机器人当前所处的格子位置,用一个长度为 2 的数组 [x, y] 表示。
String getDir() 返回当前机器人的朝向,为 “North” ,“East” ,“South” 或者 “West” 。
示例 1:
输入:
[“Robot”, “move”, “move”, “getPos”, “getDir”, “move”, “move”, “move”, “getPos”, “getDir”]
[[6, 3], [2], [2], [], [], [2], [1], [4], [], []]
输出:
[null, null, null, [4, 0], “East”, null, null, null, [1, 2], “West”]
解释:
Robot robot = new Robot(6, 3); // 初始化网格图,机器人在 (0, 0) ,朝东。
robot.move(2); // 机器人朝东移动 2 步,到达 (2, 0) ,并朝东。
robot.move(2); // 机器人朝东移动 2 步,到达 (4, 0) ,并朝东。
robot.getPos(); // 返回 [4, 0]
robot.getDir(); // 返回 “East”
robot.move(2); // 朝东移动 1 步到达 (5, 0) ,并朝东。
// 下一步继续往东移动将出界,所以逆时针转变方向朝北。
// 然后,往北移动 1 步到达 (5, 1) ,并朝北。
robot.move(1); // 朝北移动 1 步到达 (5, 2) ,并朝 北 (不是朝西)。
robot.move(4); // 下一步继续往北移动将出界,所以逆时针转变方向朝西。
// 然后,移动 4 步到 (1, 2) ,并朝西。
robot.getPos(); // 返回 [1, 2]
robot.getDir(); // 返回 “West”
提示:
2 <= width, height <= 100
1 <= num <= 10^5
move ,getPos 和 getDir 总共 调用次数不超过 10^4 次。
仍然是简单的模拟题,不过要注意方向否则很容易被绕晕。
class Robot {
public:
int d;
vector<string> dirtation={"East","North","West","South"};
int dir[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
//把他的坐标图在脑中反转成我们常用的形式更好操作
int row,col;
int x,y;
Robot(int width, int height) {
x=y=d=0;
row=width,col=height;
}
void step(int num) {
int c=2*row+2*col-4;
//这里的c是周长,当我们走刚好一个周长的时候正好走一圈
//此时就需要根据坐标来判断方向
num%=c;
if(!num&&!x&&!y){
d=3;
//如果num就是周长并且我们刚好位于原点,很容易想到此时的方向
}
while(num--){
int tx=x+dir[d][0];
int ty=y+dir[d][1];
if(tx<0||ty<0||tx>=row||ty>=col){
d=(d+1)%4;
tx=x+dir[d][0];
ty=y+dir[d][1];//越界了就改变方向注意要先改变方向再改变坐标
}
x=tx;
y=ty;
}
}
vector<int> getPos() {
return {x,y};
}
string getDir() {
return dirtation[d];
}
};