目录
一、广度优先搜索(BFS)原理
广度优先搜索是一种图搜索算法,它通过逐层遍历图的节点来查找目标节点。该算法从起始节点开始,先访问起始节点,然后访问起始节点的所有邻居节点,接着再访问这些邻居节点的邻居节点,以此类推,直到遍历完所有可达节点。为了实现逐层遍历,我们通常使用队列来保存待访问的节点。
图的广度优先搜索的过程与二叉树的层序遍历是完全一致的,BFS其实就是二叉树的层序遍历算法的推广。
二、广度优先搜索应用场景
广度优先搜索在很多领域都有广泛的应用,包括但不限于:
- 图的遍历:用于遍历图中的所有节点,查找特定节点或找到从起始节点到目标节点的最短路径。
- 迷宫问题:用于找到从起点到终点的最短路径,或者找到是否有路径可以从起点到达终点。
- 社交网络分析:用于查找两个用户之间的最短路径或共同的联系人。
- 网络路由:用于寻找最优路由和解决网络拓扑问题。
三、C++实现广度优先搜索
以下是用 C++实现广度优先搜索的简单示例代码,假设我们使用邻接表来表示图:
1. 邻接表图的定义
#define MAX_VERTICES 100
typedef int VertexType;
// 定义图的边结构
typedef struct Edge {
int adjVertex; // 与边相连的另一顶点的索引
Edge* next; // 指向下一条邻接边的指针
} Edge;
// 定义图的顶点结构
typedef struct Vertex {
VertexType data; // 顶点数据
Edge* firstEdge; // 指向第一个邻接边的指针
} Vertex;
// 定义图的邻接表结构
typedef struct Graph {
int num_vertices, num_edges; // 图中顶点的数量
Vertex vertices[MAX_VERTICES]; // 存储顶点的数组
} Graph;2. 图初始化
// 初始化图
void initGraph(Graph* graph, int num_vertices) {
graph->num_vertices = num_vertices;
graph->num_edges = 0;
for (int i = 0; i < num_vertices; ++i) {
graph->vertices[i].data = i+97; // 顶点数据字母a开始
graph->vertices[i].firstEdge = NULL; // 初始化顶点的邻接边链表为空
}
}3. 插入边
// 向图中插入一条边 (无向图)
void insertEdge(Graph* graph, int from, int to) {
if (from >= 0 && from < graph->num_vertices && to >= 0 && to < graph->num_vertices) {
// 创建新的边节点,插到from的这条链的链头
Edge* newEdge = (Edge*)malloc(sizeof(Edge));
newEdge->adjVertex = to;
newEdge->next = graph->vertices[from].firstEdge;
// 更新顶点的邻接边链表
graph->vertices[from].firstEdge = newEdge;
// 创建新的边节点,插到to的这条链的链头
Edge* NewEdge = (Edge*)malloc(sizeof(Edge));
NewEdge->adjVertex = from;
NewEdge->next = graph->vertices[to].firstEdge;
// 更新顶点的邻接边链表
graph->vertices[to].firstEdge = NewEdge;
graph->num_edges++;
}
}4. 在main函数中创建一个图
Graph graph;
initGraph(&graph, 8); //初始化8个顶点
insertEdge(&graph, 0, 2); //a-c
insertEdge(&graph, 0, 1); //a-b
insertEdge(&graph, 1, 4); //b-e
insertEdge(&graph, 1, 3); //b-d
insertEdge(&graph, 2, 6); //c-g
insertEdge(&graph, 2, 5); //c-f
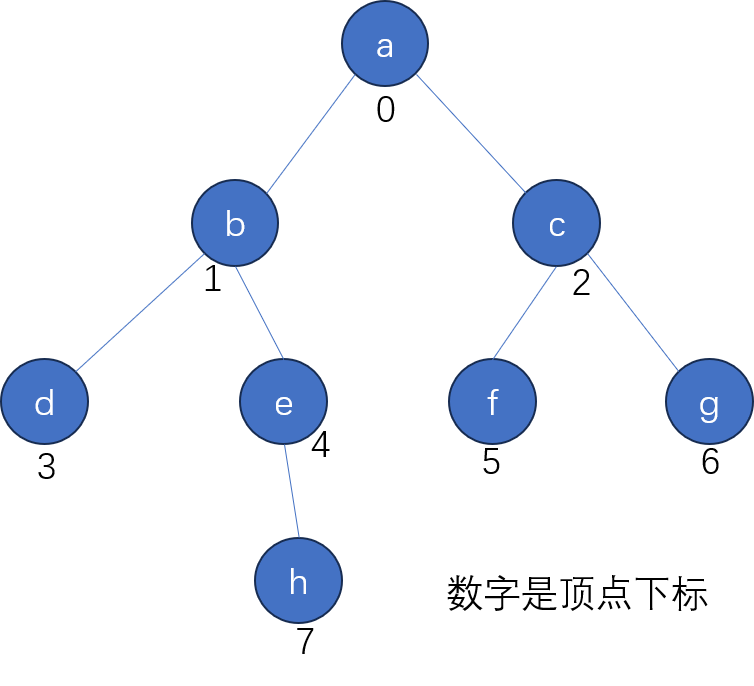
insertEdge(&graph, 4, 7); //e-h建好的图如下:
广度优先遍历的结果应该是abcdefgh
5. 访问顶点的函数
void visit(Graph graph, int v) { //访问顶点,这里是打印
cout << (char)graph.vertices[v].data;
}6. 求得顶点v的第一条边的指针
//FirstNeighbor(graph, v)是求得与v关联的第一个顶点的指针,没有就return NULL
Edge* FirstNeighbor(Graph graph, int v) {
if (graph.vertices[v].firstEdge != NULL) { //与顶点v关联的第一条边存在
return graph.vertices[v].firstEdge;
}
return NULL;
}7. BFS算法
bool visited[MAX_VERTICES]; //用于标记顶点是否被访问过,访问过为true
queue<int> q; //C++STL中的队列,创建一个辅助队列
//BFS算法
void BFS(Graph graph, int v) { //v是顶点的下标
visit(graph,v); //对顶点v的操作,可以是打印等等
visited[v] = true; //标记已访问过
q.push(v); //顶点v入队
while (!q.empty()) { //当队列不为空时
int QueueHead=q.front(); //获取当前处于队头的顶点
q.pop(); //获取队头后然后再出队
Edge* p = FirstNeighbor(graph, QueueHead); //得到上面获取的队头的指向第一条边的指针
//这层循环将访问与QueueHead关联的所有顶点
while ( p != NULL) { //p不为空说明QueueHead有关联的边
int w = p->adjVertex; //w是与v关联的顶点下标
if (!visited[w]) { //未访问
visit(graph,w); //访问顶点
visited[w] = true; //标记为已访问
//入队,每次都是先访问标记后再入队
//所以队列中的元素一定是被访问过的
q.push(w);
}
p = p->next;
}
}
}8. 对图graph进行广度优先遍历
void BFS_Traverse(Graph graph) { //对图graph进行广度优先遍历
for (int i = 0; i < graph.num_vertices; i++) { //初始化标记数组
visited[i] = false;
}
BFS(graph,0);
//若有多个连通分量,则继续调用BFS(graph,v);v是每个连通分量的任意一个顶点
}四、完整示例代码
#include<iostream>
#include<queue>
using namespace std;
#define MAX_VERTICES 100
typedef int VertexType;
// 定义图的边结构
typedef struct Edge {
int adjVertex; // 与边相连的另一顶点的索引
Edge* next; // 指向下一条邻接边的指针
} Edge;
// 定义图的顶点结构
typedef struct Vertex {
VertexType data; // 顶点数据
Edge* firstEdge; // 指向第一个邻接边的指针
} Vertex;
// 定义图的邻接表结构
typedef struct Graph {
int num_vertices, num_edges; // 图中顶点的数量
Vertex vertices[MAX_VERTICES]; // 存储顶点的数组
} Graph;
// 初始化图
void initGraph(Graph* graph, int num_vertices) {
graph->num_vertices = num_vertices;
graph->num_edges = 0;
for (int i = 0; i < num_vertices; ++i) {
graph->vertices[i].data = i+97; // 顶点数据字母a开始
graph->vertices[i].firstEdge = NULL; // 初始化顶点的邻接边链表为空
}
}
// 向图中插入一条边 (无向图)
void insertEdge(Graph* graph, int from, int to) {
if (from >= 0 && from < graph->num_vertices && to >= 0 && to < graph->num_vertices) {
// 创建新的边节点,插到from的这条链的链头
Edge* newEdge = (Edge*)malloc(sizeof(Edge));
newEdge->adjVertex = to;
newEdge->next = graph->vertices[from].firstEdge;
// 更新顶点的邻接边链表
graph->vertices[from].firstEdge = newEdge;
// 创建新的边节点,插到to的这条链的链头
Edge* NewEdge = (Edge*)malloc(sizeof(Edge));
NewEdge->adjVertex = from;
NewEdge->next = graph->vertices[to].firstEdge;
// 更新顶点的邻接边链表
graph->vertices[to].firstEdge = NewEdge;
graph->num_edges++;
}
}
void visit(Graph graph, int v) { //访问顶点,这里是打印
cout << (char)graph.vertices[v].data;
}
//FirstNeighbor(graph, v)是求得与v关联的第一个顶点的指针,没有就return NULL
Edge* FirstNeighbor(Graph graph, int v) {
if (graph.vertices[v].firstEdge != NULL) { //与顶点v关联的第一条边存在
return graph.vertices[v].firstEdge;
}
return NULL;
}
bool visited[MAX_VERTICES]; //用于标记顶点是否被访问过,访问过为true
queue<int> q; //C++STL中的队列,创建一个辅助队列
//BFS算法
void BFS(Graph graph, int v) { //v是顶点的下标
visit(graph,v); //对顶点v的操作,可以是打印等等
visited[v] = true; //标记已访问过
q.push(v); //顶点v入队
while (!q.empty()) { //当队列不为空时
int QueueHead=q.front(); //获取当前处于队头的顶点
q.pop(); //获取队头后然后再出队
Edge* p = FirstNeighbor(graph, QueueHead); //得到上面获取的队头的指向第一条边的指针
//这层循环将访问与QueueHead关联的所有顶点
while ( p != NULL) { //p不为空说明QueueHead有关联的边
int w = p->adjVertex; //w是与v关联的顶点下标
if (!visited[w]) { //未访问
visit(graph,w); //访问顶点
visited[w] = true; //标记为已访问
//入队,每次都是先访问标记后再入队
//所以队列中的元素一定是被访问过的
q.push(w);
}
p = p->next;
}
}
}
void BFS_Traverse(Graph graph) { //对图graph进行广度优先遍历
for (int i = 0; i < graph.num_vertices; i++) { //初始化标记数组
visited[i] = false;
}
BFS(graph,0);
//若有多个连通分量,则继续调用BFS(graph,v);v是每个连通分量的任意一个顶点
}
int main() {
Graph graph;
initGraph(&graph, 8); //初始化8个顶点
insertEdge(&graph, 0, 2); //a-c
insertEdge(&graph, 0, 1); //a-b
insertEdge(&graph, 1, 4); //b-e
insertEdge(&graph, 1, 3); //b-d
insertEdge(&graph, 2, 6); //c-g
insertEdge(&graph, 2, 5); //c-f
insertEdge(&graph, 4, 7); //e-h
BFS_Traverse(graph);
return 0;
}
五、运行结果
结果完全正确!!!