目录
一、前言
1、例题
有大学生刘昊、小王、阿三、蛋仔四人,想要去能力有限责任公司面试程序员的工作。该公司的HR对他们进行面试,问了些许问题,这是四人的相关回答。
A.刘昊:我家财万贯,一表人才,从小被家里人培养出性格随和的性格,业务能力与和人打交道的能力也还不错,不过在大学里面挂过很多次科,请老板信任我!
B.小王:大学里我学了特别多的东西,并且能够熟练运用这些知识到业务中,但是我是一个特别固执的人,我从来不会在意别人跟我说什么,让我去做。如果你也可以像我一样,那我觉得这件事情,太酷啦!
C.阿三:我是一个歪果仁,可能与人交流不大行,但是我写的代码嘎嘎厉害,身体非常强壮,大学里面还拿过奖学金,为人处世很随性。
D.蛋仔:我的身体很结实,在大学期间和其他同学打过架,被记过了一次,从此之后痛改前非,现在与人聊天不会轻易动怒。在学校里我天天锻炼身体,不过绩点有点低,但是这些都是可以后天学习的,希望老板能够选我进单位。
假如你是能力有限责任公司的HR,你会选择优先录取谁?其次呢?
2、层次分析法用途
得咧,尴尬了,压根不知道录取谁。感觉谁都有缺点,谁都有优点,真是让人纠结!
我们注意到,人在这个选择的过程中,并不能给出确切的量对自己的选择进行准确的描述,即人是凭借“感觉”进行选择的。“感觉”是一个模糊量,这种模糊量仅对于单层单一因素比较下的选择具有现实意义,而对于类似此题的情况就显得很难操作了。
所以,我们需要将“感觉”这一模糊量进行量化,从而得出各层因素以及各目标之间的“量化关系”,使得它们的比较具有实际意义并具有可操作性,从而帮助我们选择出最好的结果。
而层次分析法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法,尤其适合于对决策结果难于直接准确计量的场合。
请各位读者跟随我,我们将一步一步来,把这道题解决出来!
二、层次分析法步骤
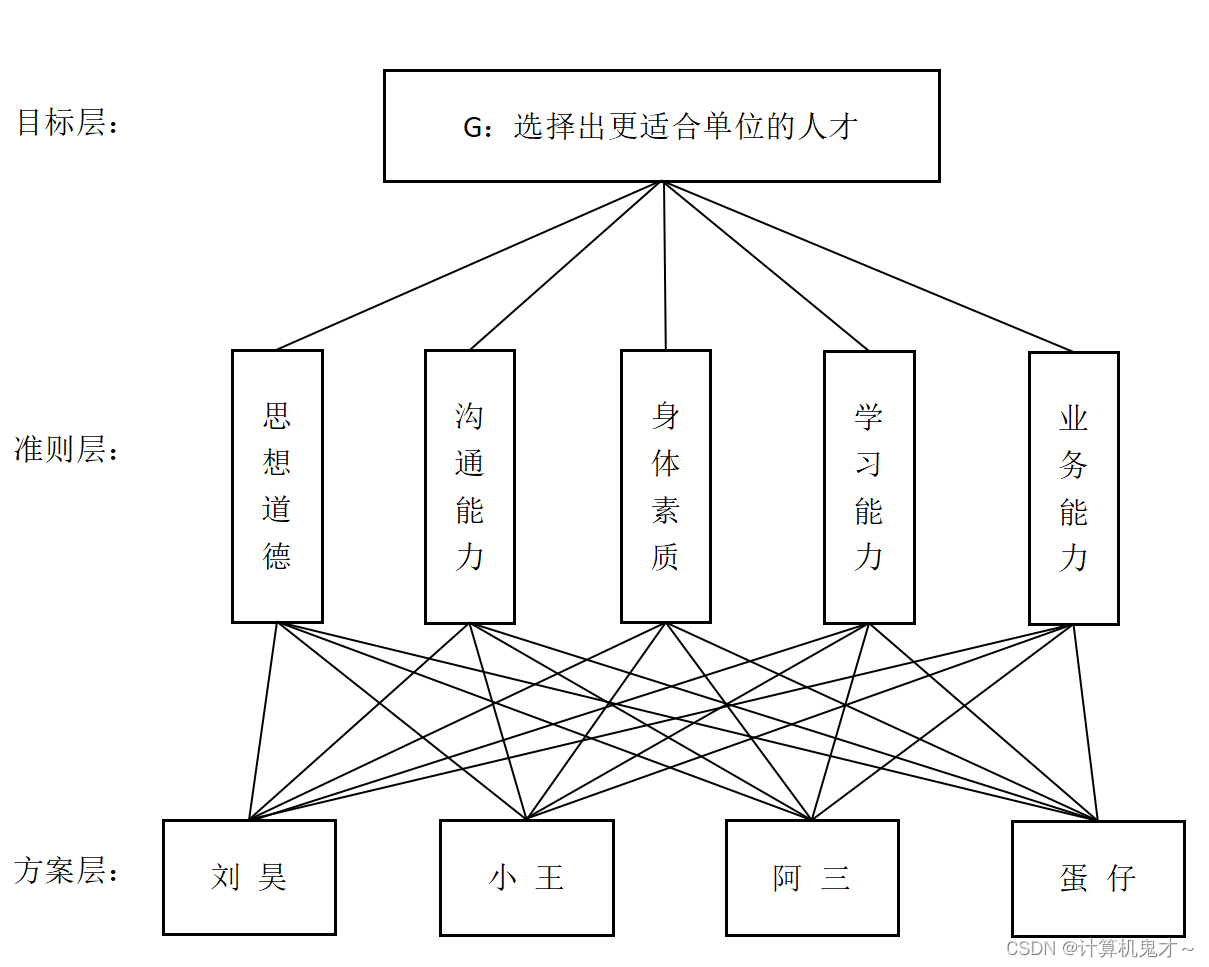
1、建立层次结构图
层次分析法首先把决策问题层次化。所谓层次 化根据问题的性质以及要达到的目标,把问题分解为不同的组成因素,并按各因素之间的隶属关系和关联程度分组,形成一个不相交的层次。我们分析实际问题中各因素之间的关系,建立实际问题的递阶层次结构.一般分为三层:目标层、准则层、方案层(或对象层)。
在本题中,我们按照此思路构建层次结构图:
目标层:替公司选出最合适的人才。
准则层:影响公司选择人才的因素有:c1:思想道德、c2:沟通能力、c3:身体素质、c4:学习能力、c5:业务能力。
方案层:设三个方案分别为:A1:刘昊、A2:小王、A3:阿三、A4:蛋仔
2、构造两两比较矩阵
在建立递阶层次结构后,上下层元素间的隶属关系就被确定了。假设以上一层次元素G为准则,所支配的下一层次的关系为c1,c2,…,cn,我们的目的是要按它们对于准则G相对重要性赋予c1,c2,…,cn相应的权重。对于有些问题可以直接给出权重,如学生的考试成绩、某工程的投资额……。但在大多数社会经济活动中,尤其是较复杂的问题中,元素的权重无法直接获得,这就需要通过适当的方法导出它们的权重。AHP所用导出权重的方法就是两两比较方法。
两两比较法具体方法是:当以上一层次某个因素C作为比较准则时,可用一个比较标度aij来表达下一层次中第i个因素与第j个因素的相对重要性(或偏好优劣)的认识。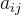
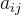
| 元素 | 标度 | 规 则 |
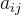 | 1 | 以上一层某个因素为准则,本层次因素i与因素j相比, 具有同样重要。 |
| 3 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j稍微重要。 | |
| 5 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j明显重要。 | |
| 7 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j强烈重要。 | |
| 9 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j极端重要。 |
当然了,也可以用其他数字,不过要保证在1-9之内
比较判断矩阵的特点:①

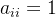
引例中, 以为单位选择出更适合单位的人才为准则(G), 它支配着5个因素: 思想道德(c1)、沟通能力(c2)、身体素质(c3)、学习能力(c4)、业务能力(c5)五个因素作出成对比较,得到比较判断矩阵:
| G | c1 | c2 | c3 | c4 | c5 |
| c1 | 1 | 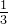 | 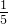 | 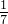 | 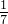 |
| c2 | 3 | 1 | 1 | 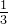 | 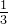 |
| c3 | 5 | 1 | 1 | 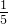 | 1 |
| c4 | 7 | 3 | 5 | 1 | 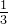 |
| c5 | 7 | 3 | 1 | 3 | 1 |
看的出来,我们以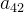
同理,我们也可以构建出每一个能力的两两比较矩阵,对于思想道德层面,刘昊肯定要比打架被记过的蛋仔强,所以我们拟定这个矩阵的a14=7,同理,我们可以构造出c1、c2……c5的相关矩阵。
| c1 | A1 | A2 | A3 | A4 |
| A1 | 1 | 5 | 2 | 7 |
| A2 | 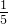 | 1 | 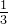 | 2 |
| A3 | 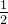 | 3 | 1 | 5 |
| A4 | 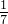 | 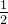 | 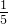 | 1 |
| c2 | A1 | A2 | A3 | A4 |
| A1 | 1 | 5 | 7 | 3 |
| A2 | 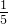 | 1 | 1 | 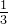 |
| A3 | 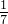 | 1 | 1 | 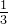 |
| A4 | 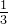 | 3 | 3 | 1 |
| c3 | A1 | A2 | A3 | A4 |
| A1 | 1 | 2 | 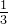 | 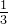 |
| A2 | 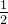 | 1 | 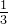 | 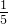 |
| A3 | 3 | 3 | 1 | 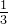 |
| A4 | 3 | 5 | 3 | 1 |
| c4 | A1 | A2 | A3 | A4 |
| A1 | 1 | 5 | 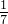 | 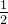 |
| A2 | 5 | 1 | 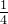 | 3 |
| A3 | 7 | 4 | 1 | 5 |
| A4 | 2 | 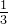 | 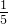 | 1 |
| c5 | A1 | A2 | A3 | A4 |
| A1 | 1 | 2 | 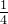 | 2 |
| A2 | 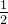 | 1 | 3 | 3 |
| A3 | 4 | 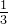 | 1 | 4 |
| A4 | 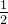 | 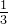 | 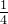 | 1 |
大家看一下,小编构造的两两比较矩阵是否合理,如果有异议,请在评论区提出您宝贵的意见哦!
3、确定相对权重向量
确定权重向量有两种方法,不过在此之前,我们要先了解归一化向量的含义。如果一个向量为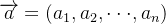
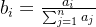
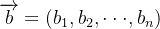
①特征根法
设A是因素c1,c2,c3…,cn对目标O的两两比较矩阵,如果A是一致阵,则A有唯一非零特征根

如果A不是一致阵,但在不一致的容许范围内,Saaty等人提出用A的最大特征根
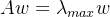
MATLAB里求特征值和特征向量的函数为:[v,d]=eig(A),小编给大家展示一下求G到c矩阵的特征值与特征向量:
A=[1 1/3 1/5 1/7 1/7;3 1 1 1/3 1/3;5 1 1 1/5 1;7 3 5 1 1/3;7 3 1 3 1];
[v,d]=eig(A)
结果为:
最大特征值为5.6020,所以对应的向量为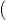
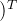
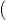
②和法
按矩阵的每一列进行归一化后,再按行求和,得到一个新的一维列向量,再对这个新的一维列向量进行归一化即可。
4、一致性检验
在实际中 ,用1-9比例标度构造构造一致阵是不太容易的,大多数3阶及3阶以上的两两比较矩阵不是一致阵.事实上只要不一致程度在一定的容许范围内,就认为构造的正互反矩阵是合适的。Saaty给出衡量比较矩阵不一致程度的指标:
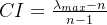
CI=0,有完全的一致性;CI接近于0,有满意的一致性;CI 越大,不一致越严重
参考随机一致性指标RI为:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| RI | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
在例题中,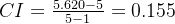
| G | c1 | c2 | c3 | c4 | c5 |
| c1 | 1 | 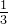 | 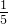 | 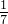 | 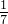 |
| c2 | 3 | 1 | 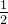 | 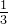 | 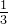 |
| c3 | 5 | 2 | 1 | 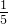 | 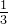 |
| c4 | 7 | 3 | 5 | 1 | 1 |
| c5 | 7 | 3 | 3 | 1 | 1 |
如此算出来的CI值为0.046,符合题目要求!同理,我们也要对关于能力的五个两两比较矩阵进行一致性检验,由于都是小编乱编的数字,肯定有些许的不合理,这五个矩阵很多都不能通过检验,需要我们重新构造,但是小编为了节省篇幅,假装这五个矩阵都通过了一致性检验,并且G对c的矩阵我们也使用最初的那一个(懒得再算了)。
5、计算层次总排序权值和一致性检验
总排序的权值计算方法为:
准则层c对目标层G的权重w(下面计算中用a代替),及方案层A对准则层c的权重B1、B2、B3,由此得到方案层A对目标层G的总层次排序权值。
以B1为例,其对总目标的权值为a1*B11+a2*B12+……a5*B15。
第二层对第一层的权向量w=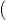
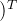

| c1 | A1 | A2 | A3 | A4 |
| A1 | 1 | 5 | 2 | 7 |
| A2 | 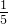 | 1 | 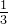 | 2 |
| A3 | 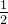 | 3 | 1 | 5 |
| A4 | 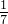 | 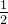 | 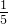 | 1 |
同理方案层对c1、c2、c3、c4和c5的特征向量即权值如下矩阵B:
| c1 | c2 | c3 | c4 | c5 | |
| A1 | 0.4681 | 0.5687 | 0.1360 | 0.1334 | 0.2215 |
| A2 | 0.2084 | 0.1106 | 0.0829 | 0.2410 | 0.4002 |
| A3 | 0.2697 | 0.0834 | 0.2648 | 0.5262 | 0.8738 |
| A4 | 0.0538 | 0.2374 | 0.5163 | 0.0994 | 0.3276 |
 | 5.1825 | 4.2506 | 4.1315 | 5.5503 | 6.4082 |
B=[0.4681 0.5687 0.1360 0.1334 0.2215;
0.2084 0.1106 0.0829 0.2410 0.4002;
0.2697 0.0834 0.2648 0.5262 0.8738;
0.0538 0.2374 0.5163 0.0994 0.3276]
w=[0.0365;0.1089;0.15866;0.3258;0.3734]
Choice=B*w结果为:
所以最后结果为:优先选阿三,其次是蛋仔,第三是小王,最后是刘昊。
看来只要技术足够硬,其他的问题都可以被稍稍忽略,而不管道德、性格还是身体素质,但是技术不过关,照样不容易被录取是,毕竟,菜是原罪。
层次总排序的一致性比率可以检测总体是否合理,公式为:
式子中:
a为准则层G对目标层c的权重w;CIk为c层对G层的一致性指标,前表已列出;RIk为随机一致性指标,此处方案有4个,则RI为0.90;
好的,本期的数学建模课就到此结束啦,层次分析法不知道观众老爷们有没有学会呢?麻烦觉得小编写的博客有帮助的老爷们给小编一个免费的小心心好嘛?