C++日常刷题积累
今日刷题汇总 - day018
1、压缩字符串(一)
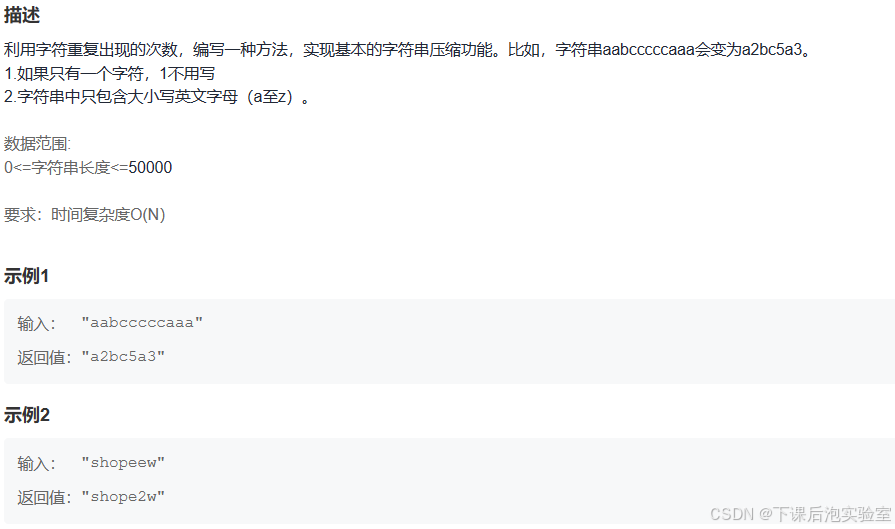
1.1、题目
1.2、思路
读完题,知道让处理一组英文字符串,完成压缩功能,压缩规则满足保持字符串的顺序将多余相邻的字符压缩以数字字符表示当前被压缩的字母个数,其中注意如果只有一个字符,1不用写。通过分析示例和题目规则,想到蛮力法,遍历字符串利用一个新字符串retstr接收遇到的字母进行尾插,统计相邻字母的个数到count中,然后转字符串尾插在字母后,然后处理重复的字母直接++count次不作任何处理知道遇见下一个不同字母即可,然后count小于1也不用管,直到遍历结束即可。接下来,就是程序实现。
1.3、程序实现
按照思路分析,完成程序即可。主要在于处理一些细节如边界控制,相同的直接统计个数和让遍历的下标++,然后处理大于1的个数尾插使用to_string(count),另外需要重置计数器为1,才进入下次循环。
class Solution {
public:
string compressString(string param) {
string retstr;
int count = 1;
for (int i = 0; i < param.size(); i++)
{
while (i + 1 < param.size() && param[i + 1] == param[i])
{
count++;
i++;
}
retstr += param[i];
if (count > 1)
{
retstr += to_string(count);
}
count = 1; // 重置计数器
}
return retstr;
}
};
2、chika和蜜柑
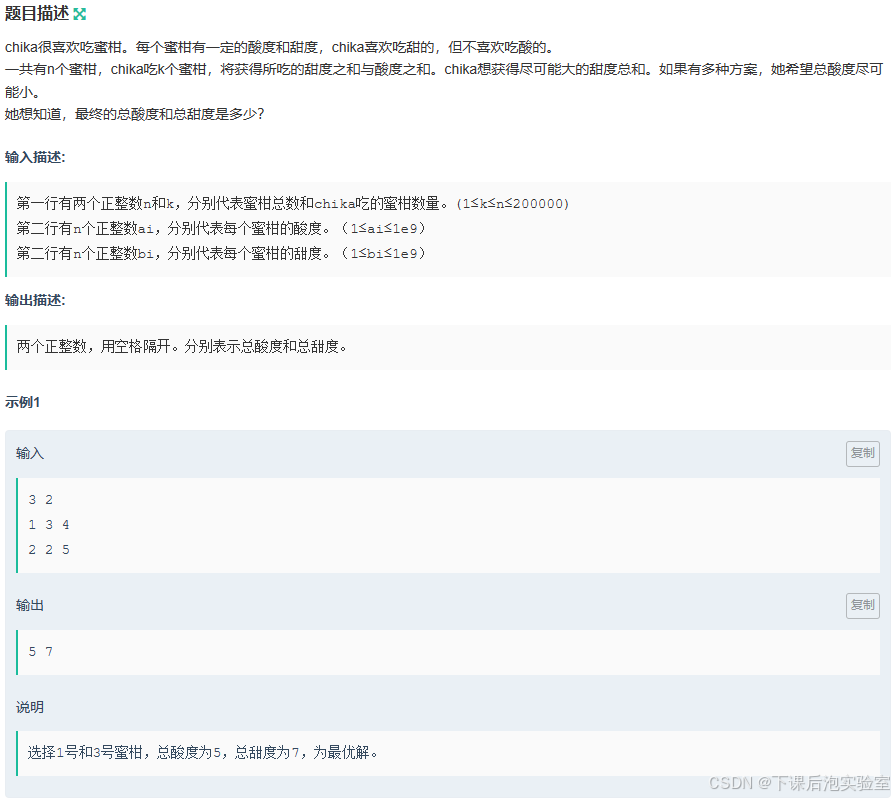
2.1、题目
2.2、思路
读完题,想到跟上次比那名居的桃子类似,但是这里并没有限制持续时间等条件,这里是任意挑选k不使用滑动窗口,所以利用排序的思想,将每个橘⼦按照甜度由⾼到低排序,相同甜度的橘⼦按照酸度由低到⾼排序。满足尽可能地甜度高。然后提取排序后的前k个橘⼦就得到最好地选择方案了。那么接下来,就是程序实现。
2.3、程序实现
首先,按照题目要求完成输入n,k代表蜜柑总数和chika吃的蜜柑数量,然后这里为了方便描述甜度和酸度这里使用pair,然后就可以输入数组arr中即可。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10;
typedef pair<int, int> PII; // <酸度,甜度>
PII arr[N];
int main()
{
int n, k;
cin >> n >> k;
for(int i = 0; i < n; i++)
cin >> arr[i].first;
for(int i = 0; i < n; i++)
cin >> arr[i].second;
//sort
//求前k个蜜柑甜度和酸度和
return 0;
}
接下来就是排序地思路,需要满足题目中尽可能地甜和不酸,那么这里可以采用lambda表达式与sort结合的方式处理即可。lambda实际上可以理解为仿函数,使其sort的执行逻辑更加方便了。
[&] 表示捕获列表,这里使用 & 表示捕获外部作用域中所有变量的引用。但在这个 lambda 表达式中,实际并没有使用到外部变量,所以 [](不捕获任何变量)或 [&] 都是可以的。
(const PII& a, const PII& b) 是 lambda 表达式的参数列表,表示这个函数对象接受两个 PII 类型的常量引用作为参数。
函数体 {} 中定义了比较逻辑:首先比较两个元素的甜度(a.second 和 b.second),如果甜度不同,则甜度较大的元素被认为更大(这里使用了 >,意味着排序后甜度是降序的)。如果甜度相同,则比较酸度,酸度较小的元素被认为更大(这里使用了 <,但注意这是为了保持甜度相同时的稳定性,实际上排序的主要依据是甜度)。
sort(arr, arr + n, [&](const PII& a, const PII& b){
if(a.second != b.second)
return a.second > b.second;
else
return a.first < b.first;
}
);
否则,不然就自己单独再封装一个比较逻辑的函数,回调到sort也行,一样的,所以综合考虑lambda这里会更好。也是处理类似逻辑比较常用的方法之一。
// 自定义比较函数
bool compare(const PII& a, const PII& b) {
if (a.second != b.second) {
return a.second > b.second; // 甜度降序
} else {
return a.first < b.first; // 甜度相同时,酸度升序
}
}
// 使用自定义比较函数进行排序
sort(arr, arr + n, compare);
除此之外,对于自定义封装的函数又恰好是比较元组类型的值,可以使用tie的逻辑实现,但是要清楚比较对象之间的关系。
注意包含头文件#include < tuple > // 对于 std::tie
// 自定义比较函数
bool compare(const PII& a, const PII& b) {
return tie(b.second, a.first) < tie(a.second, b.first);
// 注意这里的 b.second 和 a.first 是为了得到甜度降序,酸度相同则酸度升序的效果
// 但实际上,对于这种情况,更直观的方式直接比较定义,更具有阅读性
}
// 使用自定义比较函数进行排序
sort(arr, arr + n, compare);
最后,遍历前k个蜜柑获取甜度和酸度和,然后按照题目要求的格式输出即可。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10;
typedef pair<int, int> PII; // <酸度,甜度>
PII arr[N];
int main()
{
int n, k;
cin >> n >> k;
for(int i = 0; i < n; i++)
cin >> arr[i].first;
for(int i = 0; i < n; i++)
cin >> arr[i].second;
sort(arr, arr + n, [&](const PII& a, const PII& b){
if(a.second != b.second)
return a.second > b.second;
else
return a.first < b.first;
}
);
long long s = 0, t = 0;
for(int i = 0; i < k; i++)
{
s += arr[i].first;
t += arr[i].second;
}
cout << s << " " << t << endl;
return 0;
}
3、 01背包
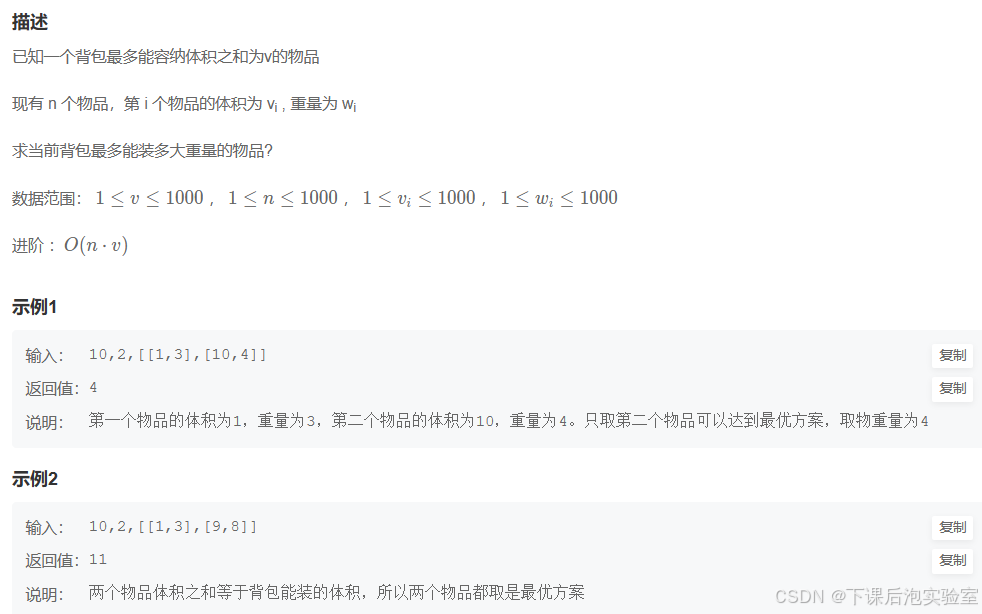
3.1、题目
3.2、思路
读完题知道,0/1背包问题是算法课的经典题型了,通常涉及贪心和dp动态规划法,简单说就是尽可能让包不超重情况下,装最多的物品。所以这里分析题目和示例得知,采用动态规划法分析:状态表示和状态转移方程。
状态表示:dp[i][j]:表示从前 i 个物品中挑选,总体积不超过 j 的情况下,最⼤重量是多少。
推导状态转移方程,根据「最后⼀步」的状况,需要分情况讨论:
(1)、当第i个物品不被选时,就是i-1个物品中挑选,且体积不超过j,此时满足dp[i][j] = d[i-1][j];
(2)、当选择第i 个物品时,那么就只能去前i - 1 个物品中,挑选总体积不超过j - v[i]的物品。此时dp[i][j] = dp[i - 1][j - v[i]] + w[i] 。但是这种状态不⼀定存在,因此需要特判⼀下。
综上所述:
状态转移⽅程为: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])
那么接下来,就是程序实现。
3.3、程序实现 – dp
首先,题目已经给了几个参数:
int V 表示背包的最大容量。
int n 表示物品的数量。
vector<vector >& vw 是一个二维向量,其中vw[i][0]表示第i个物品的重量,vw[i][1]表示第i个物品的价值。
然后按照思路分析的需求定义dp数组,然后,在内层循环中依次放入物品,对于每个容量j,如果当前容量j大于等于当前物品的重量vw[i][0],则有两种选择:
1.不装入当前物品,此时背包的价值为dp[j](即前i-1个物品在容量j下的最大价值)。
2.装入当前物品,此时背包的价值为dp[j - vw[i][0]] + vw[i][1](即前i-1个物品在容量j - vw[i][0]下的最大价值,加上当前物品的价值)。
使用max函数比较这两种选择,取较大值作为dp[j]的值,即dp[j] = max(dp[j], dp[j - vw[i][0]] + vw[i][1]);。
最终,dp[V]存储的就是在背包容量为V时,能够装载的最大价值,将其作为函数的返回值。
class Solution {
public:
int dp[1010] = { 0 };
int knapsack(int V, int n, vector<vector<int> >& vw) {
for (int i = 0; i < n; i++)
{
for (int j = V; j >= vw[i][0]; j--)
{
dp[j] = max(dp[j], dp[j - vw[i][0]] + vw[i][1]);
}
}
return dp[V];
}
};