0 前言

🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升，传统的毕设题目缺少创新和亮点，往往达不到毕业答辩的要求，这两年不断有学弟学妹告诉学长自己做的项目系统达不到老师的要求。

为了大家能够顺利以及最少的精力通过毕设，学长分享优质毕业设计项目，今天要分享的是

🚩 ** 单片机LSRB算法的走迷宫小车 **

🥇学长这里给一个题目综合评分(每项满分5分)

• 难度系数：4分
• 工作量：4分
• 创新点：3分

🧿 选题指导, 项目分享：

https://gitee.com/dancheng-senior/project-sharing-1/blob/master/%E6%AF%95%E8%AE%BE%E6%8C%87%E5%AF%BC/README.md

1 简介

这是一款使用LSRB算法解决迷宫的线迷宫机器人。与许多机器人不同，这是通过使用 IR 传感器阵列来完成的，但我找到了一种仅使用 3 个 IR 传感器来解决迷宫问题的方法。与此同时还节省了很多经费，因此这个项目也可以说是爱好者的一个简单且更便宜的选择。

2 主要器件

• 对称底盘
• 电机驱动器
• 陀螺仪（可选）
• 60 RPM 直流电机
• 车轮
• 红外传感器
• Arduino Pro Mini

3 实现效果

构造

4 硬件设计

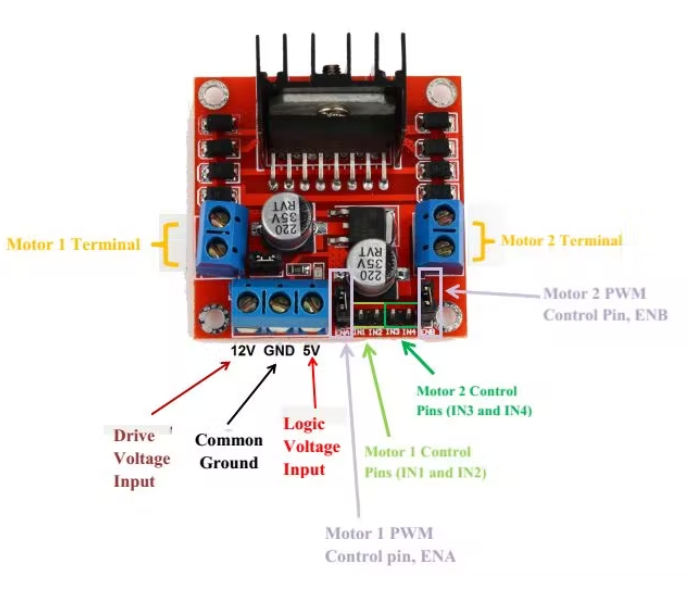
马达驱动器(L298N)

这将用于驱动直流电机。L298N是双通道的，意思是它可以同时控制两个电机的方向。

Mpu 6050

MPU6050是6轴加速度加陀螺仪模块。这意味着它可以测量 X、Y 和 Z 方向的加速度，还可以测量运动中身体的偏航、俯仰和滚动。

60 RPM 直流电机

这些电机将用于移动机器人。为什么选择 60 RPM 电机？好吧，如果您正在入门，最好从慢速马达开始。速度慢的机器人更稳定，更容易控制。对于许多强劲的 RPM，电机将难以控制（为此您需要强大的 PID 控制器）。因此，要开始使用，建议使用 60 RPM 直流电机。

红外传感器

这些传感器将在检测交叉路口类型方面发挥重要作用。

Arduino Pro mini

这将是我们机器人的大脑。算法的所有处理和计算都将在这个微控制器中进行。

5 软件说明

“LSRB”算法

这是机器人解决迷宫的算法。在“LSRB”中，L 代表“LEFT”，S 代表“STRAIGHT”，R 代表 RIGHT，B 代表“BACK”或 BACKWARD。这些 LEFT、RIGHT、STRAIGHT 和 BACK 是机器人遵循的方向。该算法简单直接。在该算法中，向左方向具有最高优先级，而后（U 形转弯）方向具有最低优先级。让我们看看这个算法是什么样子的：

• 第 1 步：只要有可能转弯，请始终跟随左转
• 第 2 步：如果无法向左走，请直接走。
• 第 3 步：如果 LEFT 和 STRAIGHT 都不可能，请选择 RIGHT。
• 第 4 步：如果 LEFT、STRAIGHT 和 RIGHT 都不可能返回（或者这意味着要掉头）

这意味着无论何时机器人在转折点或十字路口，它总是尽可能向左走。如果 LEFT 不可能，那么 STRAIGHT，如果两者都不可能，那么 RIGHT。如果所有三个转弯都不可能，那么只能返回。这是您唯一需要了解的 LSRB 算法。基于此，有 8 种可能的情况：

• 1.Simple 或 Straight lane ：这里 LEFT 是不可能的，但 STRAIGHT 路径是。所以机器人将遵循直线路径。
• 2.左转（仅限左）：顾名思义，这是左转，所以这里可以左转。根据 LSRB 算法，机器人应尽可能向左走。所以机器人会在这里左转。
• 3.右转（仅右转）：同样顾名思义，这是一个右转，所以左和直路径都是不可能的，所以根据 LSRB 算法机器人将右转。
• 4.T相交(T)：这个相交的形状像T，所以叫T相交。如图所示，Robot 可以左转。所以通过算法机器人会左转。
• 5.左 T 路口（直或左）：再次通过图像，我们可以看到机器人可以走左路，所以机器人会在这里左转。
• 6.Right T 交点（直或右）：这里不可能向左，但直路径是。所以机器人会左转
• 7.Dead End：这里 LEFT、STRAIGHT 和 RIGHT 这三个都不可能。所以机器人会在这里掉头。
• 8.四车道交叉口（Cross）：此处再次通过图像左转是可能的，因此机器人将在此处左转。

最后，迷宫结束：迷宫在这里结束，所以机器人会停在这里。

现在让我们看一下如何将其转换为代码：

//LSRB ALGORITHM

IR1 = <PIN 1>
IR2 = <PIN 2>
IR3 = <PIN 3>

void setup 
{
  DECLARE IR1 IR2 AND IR3 AS INPUTS
}

void loop 
{
  IR1 = digitalRead(<PIN 1>)
  IR2 = digitalRead(<PIN 2>)
  IR3 = digitalRead(<PIN 3>)

  if (IR1 == LOW && IR2 == HIGH && IR3 == LOW)//Straight path
    {
     Forward();
    }

  if (IR1 == HIGH && IR2 == LOW && IR3 == LOW)//Left turn
    {
     Left();
    }

  if (IR1 == LOW && IR2 == LOW && IR3 == HIGH)//Right Turn
    {
      Right();
    }

  if (IR1 == HIGH && IR2 == LOW && IR3 == HIGH)//T Intersection
    {
      Left(); // As left is possible
    }

  if (IR1 == HIGH && IR2 == HIGH && IR3 == LOW)//Left T Intersection
    {
      Left();// As Left is possible
    }

  if (IR1 == LOW && IR2 == HIGH && IR3 == HIGH)//Right T Tntersection
    {
     Forward();//As Straight path is possible
    }

  if (IR1 == LOW && IR2 ==LOW && IR3 == LOW)//Dead End
    {
     U_Turn(); //As no other direction is possible
    }

  if (IR1 == HIGH && IR2 == HIGH && IR3 == HIGH)//4 Lane intersection
    {
     Left(); //As no other direction is possible
    }

  if (IR1 == HIGH && IR2 == HIGH && IR3 == HIGH)//End of Maze
    {
     Stop(); //As no other direction is possible
    } 
}

代码很简单，但还有一个问题。4车道交叉口和迷宫尽头的情况似乎相似。我们的机器人如何区分 4 车道交叉口和 End of Maze？答案也很简单。让机器人走得更远一点。现在，如果传感器的值保持不变，那就结束了。但是如果左右传感器的值发生变化，那么它是一个 4 路交叉点。让我们看一下它的代码：

if (IR1 == HIGH && IR2 == HIGH && IR3 == HIGH)
    {
     Forward();
     delay(<Time>);
     Stop();

     if (IR1 == HIGH && IR2 == HIGH && IR3 == HIGH)
        {
          Serial.println("ËND OF MAZE");
          Stop();
        }
     else
        {
         Serial.println("FOUR WAY INTERSECTION");
         Left();
        }
    }

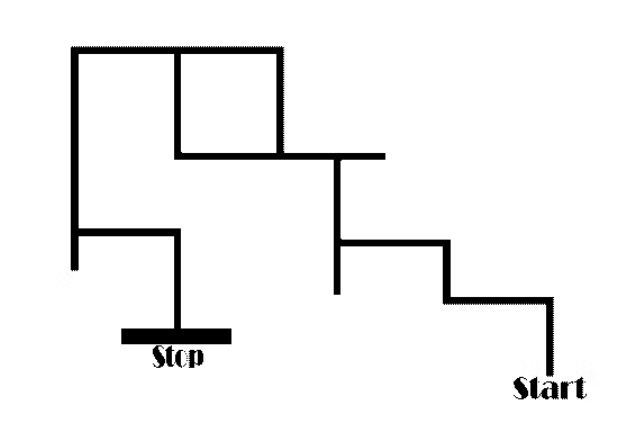
最短路径算法

这是机器人用来计算迷宫中最短路径的算法。它使用使用 LSRB 算法获取的路径并将其转换为最短路径。如何？让我们看看这是如何工作的。考虑下图中的迷宫。现在让我们在这里放置一个机器人，让我们通过 LSRB 算法可视化它的路径。我们可以通过使用 LSRB 算法，机器人将采取 LEFT、LEFT、BACK、RIGHT、STRAIGHT。简而言之，我们可以说机器人跟随 L、L、B、R、S。现在作为一个人，我们可以直接说最短路径就是这里的 RIGHT 或“R”转。但是机器人是如何做到这一点的呢？最短路径算法在这里使用了替换。这些替换如下所示：

• LBR = “B”
• LBS = “R”
• RBL = “B”
• SBL = “R”
• SBS = “B”
• LBL = “S”

现在让我们通过替换方法缩短路径。在路径 {L, L, B, R, S} 中，LBR = ‘B’ 所以 Path 现在变为 { L, B, S}。现在 LBS = ‘R’ 所以最终路径变为 { R} ，如前所述，这是正确的。现在让我们将这个算法转化为 Arduino 代码：

void CALCULATE_SHORTEST_PATH(char MAZE_ARRAY[], int SIZE_OF_ARRAY)
{
  /*ONCE THE ROBOT COMPLETES THE MAZE THE FINAL SHORTEST PATH CALCULATED
  IS STORED IN THE ROBOT MEMORY.THIS SHORTEST PATH IS USED TO COMPLETE
  THE SAME MAZE IN SHORTEST AMOUNT OF TIME.(L :LEFT, R:RIGHT, B:BACK,S:STRAIGHT)
  BELOW ARE THE FEW SUBSTITUTIONS TO CONVERT FULL MAZE PATH TO ITS 
  SHORTEST PATH:
  LBL = S
  LBR = B
  LBS = R
  RBL = B
  SBL = R
  SBS = B
  LBL = S */

  char ACTION;
  
  for(int i = 0; i <= SIZE_OF_ARRAY-2; i++)
    {
      ACTION = MAZE_ARRAY[i];
           
      if(ACTION == 'B')
        {
          if(MAZE_ARRAY[i-1]== 'L' && MAZE_ARRAY[i+1] == 'R')
            {
              MAZE_ARRAY[i] = 'B';
              MAZE_ARRAY[i-1] = 0;
              MAZE_ARRAY[i+1] = 0;
              REARRANGE(MAZE_ARRAY,SIZE_OF_ARRAY,i-1,i,i+1); 
            }

           if(MAZE_ARRAY[i-1]== 'L' && MAZE_ARRAY[i+1] == 'S')
            {
              MAZE_ARRAY[i] = 'R';
              MAZE_ARRAY[i-1] = 0;
              MAZE_ARRAY[i+1] = 0;
              REARRANGE(MAZE_ARRAY,SIZE_OF_ARRAY,i-1,i,i+1);
            }

            if(MAZE_ARRAY[i-1]== 'R' && MAZE_ARRAY[i+1] == 'L')
            {
              MAZE_ARRAY[i] = 'B';
              MAZE_ARRAY[i-1] = 0;
              MAZE_ARRAY[i+1] = 0;
              REARRANGE(MAZE_ARRAY,SIZE_OF_ARRAY,i-1,i,i+1);         
            }

            if(MAZE_ARRAY[i-1]== 'S' && MAZE_ARRAY[i+1] == 'L')
            {
              MAZE_ARRAY[i] = 'R';
              MAZE_ARRAY[i-1] = 0;
              MAZE_ARRAY[i+1] = 0;
              REARRANGE(MAZE_ARRAY,SIZE_OF_ARRAY,i-1,i,i+1);             
            }

            if(MAZE_ARRAY[i-1]== 'S' && MAZE_ARRAY[i+1] == 'S')
            {
              MAZE_ARRAY[i] = 'B';
              MAZE_ARRAY[i-1] = 0;
              MAZE_ARRAY[i+1] = 0;
              REARRANGE(MAZE_ARRAY,SIZE_OF_ARRAY,i-1,i,i+1);             
            }

            if(MAZE_ARRAY[i-1]== 'L' && MAZE_ARRAY[i+1] == 'L')
            {
              MAZE_ARRAY[i] = 'S';
              MAZE_ARRAY[i-1] = 0;
              MAZE_ARRAY[i+1] = 0;
              REARRANGE(MAZE_ARRAY,SIZE_OF_ARRAY,i-1,i,i+1);
            }
            
          i = -1;
        }
       
       delay(100);   
    }
}

最短路径算法可以用 3 个红外传感器吗？

如果您只使用 3 个红外传感器，那就很难了。为了使其工作，您必须使用 PID 算法使机器人遵循绝对直线路径。如果您的机器人遵循绝对直线路径，则只能在其中实现最短路径算法。

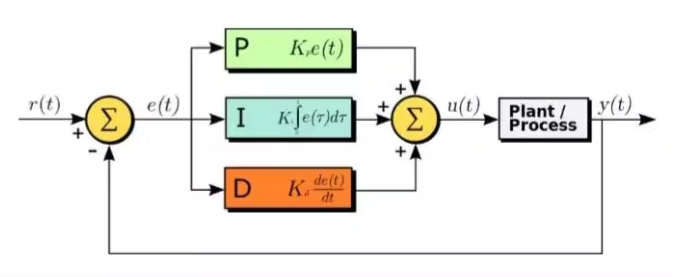
PID控制器

PID控制器中的PID代表比例积分和微分。这将在我们的机器人中用于遵循一条完全笔直的路径。先查看一下PID这个术语的意思：

1.Proportional：此项与误差（E）项成正比。误差越大，比例部分的值越大。该值负责机器人的转动。例如，如果误差很大，那么机器人的动作也会很强。所以基本上比例负责机器人的动作强度。比例的缺点是它会产生很多振荡。就像如果机器人只包含比例部分，那么车辆将继续从左到右摆动。好吧，它会直走，但会振荡很多。通过比例控制获得的增益用“KP”表示。

P = KP x Error

2. 积分：即使在微分部分消除了振荡之后，仍然存在小的偏移量。积分部分通过考虑所有误差来消除此偏移。积分项随时间增加。通过积分获得的增益用“KI”表示。

I = I + KI x Error

3 微分：微分项减少或消除了比例项产生的振荡。这将使机器人的运动更加顺畅。机器人将沿着一条直线前进，没有振荡。Derivative 获得的增益用“KD”表示。

D = KD x (Error - Previous_Error)/Time

PID 的公式由下式给出：

所以最终的PID值是通过将这些项相加得到的：

PID = P + I + D

PID 的主要目标是尽可能减少误差项。在继续编码之前，PID 控制器需要三个主要元素。

1.反馈：反馈是一个过程，其中一部分输出用作迭代中的输入。在我们的案例中，反馈是由 MPU6050 提供的。我们得到了什么样的反馈？我们得到陀螺值作为反馈。

2.Actuator：这个东西起到改变系统输出的作用。它可以是伺服电机、直流电机或任何其他电机。在我们的例子中，执行器是机器人的两个直流电机。

3.SetPoint ：这是我们想要达到的理想点或值。它是通过完全消除误差而获得的。

现在将这个理论转化为代码：

double PID_CONTROLLER(double FEEDBACK, double dt)
{
  double ERROR_VALUE;
  double PREVIOUS_ERROR_VALUE = 0;
  double SETPOINT = <desired_value>; //put the desired value decided by you here.
  double KP = <value>; //put the value you want here.
  double KI = <value>; //put the value you want here.
  double KD = <Value>; //put the value you want here.
  double P;
  double I;
  double D;
  double INTEGRAL;
  double DERIVATIVE;
  double OUTPUT_VALUE;

  ERROR_VALUE = SETPOINT - FEEDBACK; //Here the feedback is YAW from MPU6050

  P = KP*ERROR_VALUE; 

  INTEGRAL += ERROR_VALUE*dt;
  I = KI*INTEGRAL;

  DERIVATIVE += (ERROR_VALUE-PREVIOUS_ERROR_VALUE)/dt;
  D = KD*DERIVATIVE;

  OUTPUT_VALUE = P + I + D ;

  PREVIOUS_ERROR_VALUE = ERROR_VALUE;

  return OUTPUT_VALUE;
  
}

PID值的调整：
调整系统的 Kp、Ki 和 Kd 值的方法有很多，其中一种是手动调整，通过它可以轻松实现稳定性。最初，Kp、Ki 和 Kd 值设置为零。然后 Kp 值从零增加到系统开始从其平均位置振荡的点。
随着 Kp 值的增加，可以看出系统的响应逐渐增加。保持 Kp 值恒定，然后增加 Ki 值，直到从系统中可以看出，朝某个方向的小倾斜倾向于使车辆朝该方向加速。当正确获得 Kp 和 Ki 值时，则增加 Kd 值。Kd 值增加，从而显着降低了快速加速度。
适当的 KD 值会导致较小的过冲和振荡。在获得粗略的 Kp、Ki 和 Kd 值后，进行微调。以上步骤重复多次，得到增益值的最佳组合。

PID控制器

即使使用对称的底盘，您可能已经注意到机器人在沿线行驶时仍然会向左或向右移动，这是因为直流电机。爱好者使用的直流电机并不完美。没有两个电机是一样的。它们的机械结构之间总是存在细微差别。如果您的机器人遵循绝对直线路径，那么您很幸运，恭喜！但很多时候这种情况不会发生，机器人通常不会向左或向右移动。如果您不使用红外传感器阵列，这可能会影响您的最短路径算法。对 PID 的另一种需求是当您使用非常高的 RPM 电机时。

为了克服这个问题，有很多选择：

1.使用优质直流电机（不保证直线路径）

2.使用优质车轮（不保证直线路径）

3.使用高度机械精确的底盘（不保证直线路径）

4.降低一个电机的速度，使两个电机的速度完美匹配（但这样做后仍然存在微小的误差，使机器人几乎没有偏离轨道）。

5.使用旋转编码器（有时可能很好用）

6.使用PID控制器（如果编码完美，保证机器人的直线路径）。

在所有这些选项中，只有 PID 控制器可以保证机器人的绝对直线路径。

请注意，代码将仅是 LSRB 算法的实现。代码中有一个最短路径函数，您可以使用它来实现最短路径算法。您可以尝试使用该功能来实现 3 个红外传感器的最短路径。

6 最后