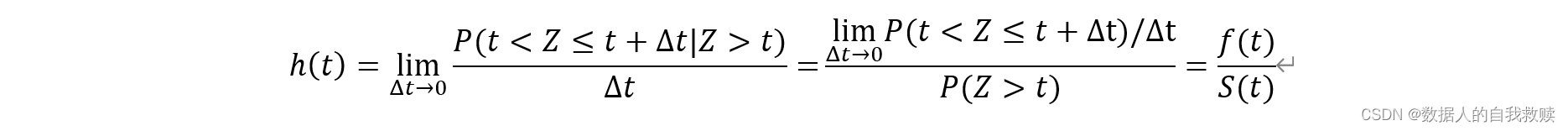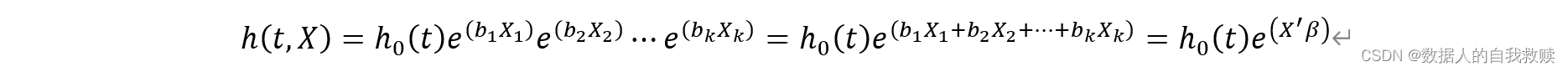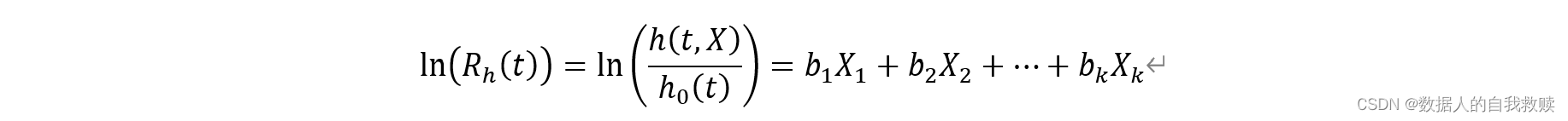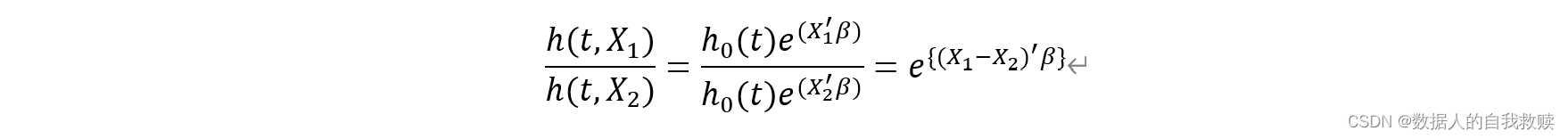目录
一、生存分析介绍
1.生存分析用途
生存分析是一种常用于医学研究的方法,但该方法最早用于武器寿命的分析,如考虑炮弹存放一年后仍可正常使用的概率。该方法可用于其他很多领域,如:
(1)职员在公司任职的时间(员工在公司待k年的概率)
(2)产品的寿命预测(可靠性)
(3)治愈某疾病所需时间(使用药物k年后病人的存活率)
2.传统方法在分析随访资料时的困难
(1)生存时间和生存结局都是我们关心的因素
- 除了生存结局之外,只要能让病人存活时间延长,这种药物也是有效的,即存活时间的延长也是我们关心的问题。
- 如果将两者均作为因变量拟合多元模型,则生存时间分布不确定(肯定不呈正态分布,在不同情况下其分布规律也不同),生存结局是0-1分布,生存时间是连续型分布,将两者拟合多元模型很困难。
(2)存在大量失访
- 失去连续(病人搬走,电话号码改变)
- 无法观察到结局事件发生(死于其他原因)
- 研究中止
(3)显然,将失访数据无论是算作死亡还是存活都不合理
3.生存分析的优劣势
(1)优势
在针对总体生存时间都比较短的疾病的研究中,生存分析比考虑结局,不考虑时间因素的Logistic模型等方法的效率要高的多。
(2)劣势
如果相应疾病的结局都非常好,比如几乎人人都可痊愈的感冒,生存分析的利用价值并不大,因为除非是特殊情况,感冒晚好两天对医生或病人来说并没有太大影响。
4.生存分析的主要研究内容
(1)描述生存过程(Kaplan-Meier方法)
- 研究人群生存状态的规律
- 研究生存率曲线的变动趋势
- 是人寿保险业的基础(从加入保险开始,每年有多少理赔事件发生,公司收多少费用才能保证不赔)
(2)生存过程影响因素分析及结果预测(Cox回归法)
- 了解哪些因素会影响生存过程
- 对生存结局加以预测(如病人还能活多久):该方法在临床医学领域应用非常广泛
5.常用术语
(1)失效事件(Failure event)
也被称为“死亡”事件或失败事件,表示观测到受访对象出现了我们所规定的结局。失效事件的认定是生存分析的重要环节,必须绝对准确。
失效事件应当由研究目的而决定,并非一定是死亡(如研究灯泡寿命),而死亡也并非一定是发生了失效事件(如肺癌患者死于其他疾病)。
(2)删失数据(截尾数据,Censored data)
终止随访不是由于失效时间发生,而是无法继续随访下去,常用符号“+”表示,如:
- 生存但中途失访:包括拒绝访问、失去联系或中途退出试验。
- 死于其它与研究无关的原因:如肺癌患者死于其他疾病,终止随访时间即为死亡时间。
- 随访截止:随访研究结束时观察对象仍存活。
(3)生存时间(Survival time)
随访观察持续的时间,按失效事件发生或失访前最后一次的随访事件记录,常用符号t表示。
根据失效事件的定义不同,生存时间可能是各种类型的指标,甚至可能不是“时间”,如:
- 设备从开始使用到失效的累计使用时间;
- 汽车的累计行驶里程。
(4)生存率(Survival rate)
生存率也称为生存函数S(t) ,指某个受访对象活过t时刻的概率,用S(t)=P(x>t) 表示,可见S(t)=1-F(t) ,其中F(t) 为生存时间的分布函数。
根据不同研究问题定义的失效事件,生存率可以是产品有效率、可靠性等。
6.生存分析方法分类
(1)参数法
首先要求观察的生存时间X 服从某一特定的分布,采用估计分布中参数的方法获得生存率P(X>t) 的估计值。
生存时间的分布F(.) 可能为指数分布、weibull 分布、对数正态分布等,这些分布曲线都有相应的生存率函数形式。只需求得相应参数的估计值,即可获得P(X>t) 的估计值和曲线。
P(X>t)=1-F(t)
(2)非参数法
实际工作中,多数生存时间的分布不符合上述常见的分布,就不宜用参数法进行分析,而应当用非参数法。
这类方法的检验假设与以往所学的非参数法一样,原假设是两组或多组的总体生存率曲线分布相同(不论总体的分布形式和参数如何)。如检验服药组和对照组的生存曲线是否有显著差异,从而判断药物疗效。
非参数法是生存数据的常用分析方法
(3)半参数法
只规定了影响因素和生存状况间的关系,但是没有对事件(和风险函数h(t) )的分布情况加以限定。
这种方法主要用于分析生存率的影响因素,属多因素生存分析方法,典型方法是Cox等比例风险模型。
二、Kaplan-Meier方法
是最基本的一种生存分析方法,例如新药组与对照组疾病疗效的比较研究
三、Cox等比例风险模型
1.模型介绍
Cox等比例风险模型属于半参数模型,与参数模型相比,该模型不能给出各时点的生存率,其对生存时间的分布无要求,可发掘在整个研究时段内对生存状况影响显著的因素,并估计出各因素对生存率的影响程度,因而应用范围更广。为了纪念Cox的贡献,统计学家把它称为Cox等比例风险模型(Cox回归模型)
2.风险函数h(t)
生存到时刻t的观察对象在时刻t的瞬间死亡率称为风险函数(hazard function)。
在比例风险模型中,假设在时点t个体出现观察结局的风险大小可以分解为两个部分:有一个基本风险量h0(t) ,代表没有任何自变量影响下的生存状况(反映病人不采取任何措施时的生存状况);第i个影响因素使得在任意一个时点t的死亡风险(风险函数值)从h0(t) 增加e(biXi) 倍,称为ht=h0(t)e(biXi) 。
因此,如果在k各因素同时影响生存过程的情况下,在时点t的风险函数值就为:
上式取对数,移项得:
- Rh(t) :k个因素影响下得新风险函数值与基本风险量之比。
- h0(t) (基准风险函数):表示个体在时点t得基准生存状况(没有任何自变量影响下的风险函数)。
- 两个人在某一特定时刻死亡风险比值如下:
- bi :与以前相同,可直接理解为Xi 的回归系数;实际含义是,当变量Xi 改变一个单位时,引起的死亡风险改变倍数的自然对数值。
- exp(bi) (相对危险度,Relative Risk):表示当变量Xi 改变一个单位时,前后两种情况下发病风险(风险函数值)之比RR=h(t,Xi+1)/h(t,Xi) ;如果RR>1则说明相应的自变量取值增加一个单位,会导致受访个体的发病/死亡风险增加若干倍;因此,RR在医学领域应用极为广泛,在该领域其使用价值高于优势比OR(odds ratio)。
四、加速失效模型
log(Z)=X'β+ε=β0+β1X1+β2X2+β3X3+ε
其中,Z0=exp(ε) 称为基准生存时间,Z=Z0e(X'β) 。