算法课程中的一道讨论题引起的思考，在未查阅到详细分析的基础上写下此文章。

在求任意两个非负整数最大公约数时，若简单使用穷举法分析，则时间复杂度如下：

使用欧几里得算法分析：

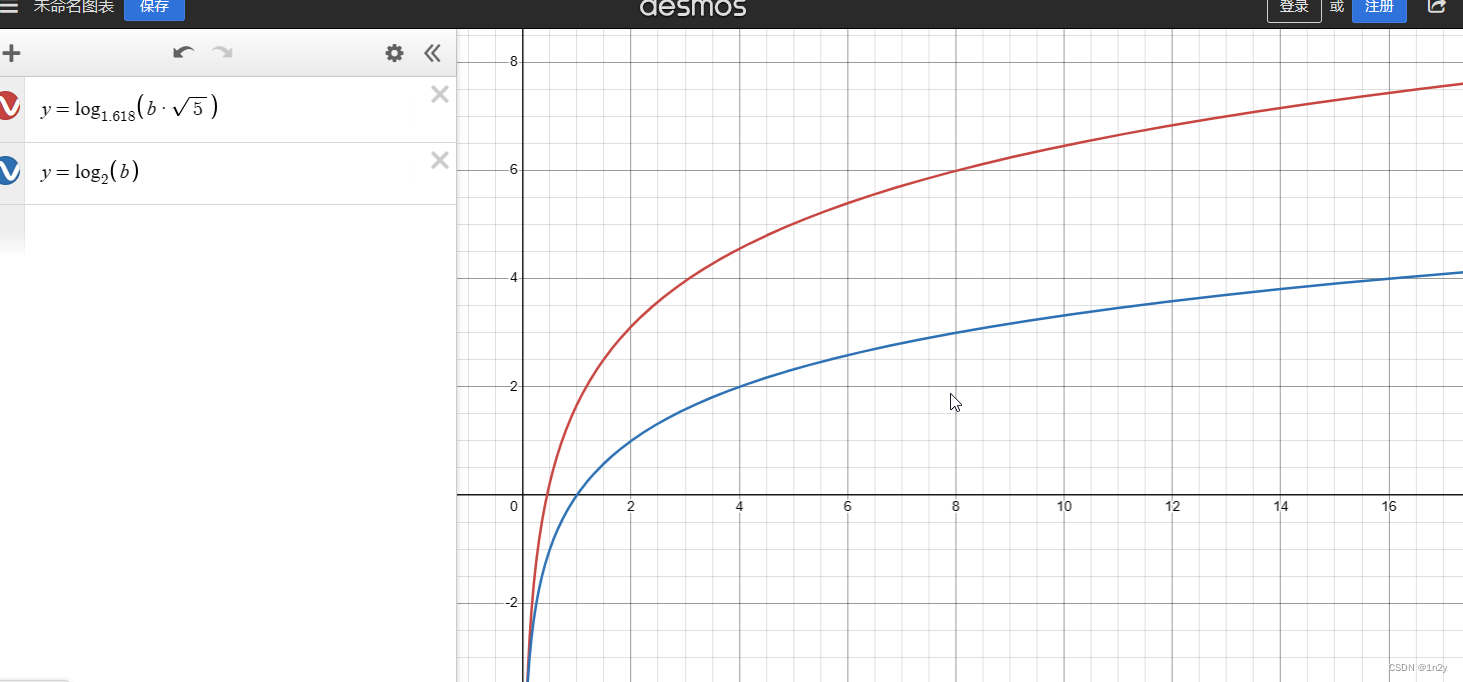
使用绘图软件对两种方法的时间复杂度进行绘图，可以观测到以下图形：

设欧几里得法与穷举法的时间复杂度的渐进函数分别为f(n) g(n)

以b=13为例，f=3.7 ;  g=7.003  ;

取a=28,b=17,

1. R=11
2. R=6
3. R=5
4. R=1
5. R=0

 共五次，而f(n)=7.56;

a=33,b=19

1. R=14
2. R=5
3. R=4
4. R=1
5. R=0

 共五次，f(n)=7.791；

例三 a=34,b=21 (Fibonacci数列的相邻项)

1. R=13
2. R=8
3. R=5
4. R=3
5. R=2
6. R=1
7. R=0

共七次 此时f(n)=g(n)

初步得出结论，Fibonacci算法求得的时间复杂度

是欧几里得算法计算的次数上限。

进一步分析得知，对于欧几里得算法的a，b  当a<=Fn时，对于b<=Fn-1 ,时，gcd运算次数的上限的划分点（如六次运算和七次运算的分解数值）恰好是Fibonacci的Fn-1项所对应的数值；

比如当21<=b<=a<=34, 最大的运算次数为8次，而对于Fibonacci的时间复杂度函数，当b=21时的计算结果也为7.9999≈8.0；

而当欧几里德算法的输入是Fibonacci序列中连续的两项时，算法执行时间是同等规模下的最坏情况执行时间，如例三所示。

总结：当a=Fn时，对于b=Fn-1 ,时，gcd运算次数的上限的划分点为Fibonacci的Fn-1项所对应的数值，小于或大于均不会得到此结论。