1、图的定义与操作
A 定义
图是有顶点集合(Vertex)及顶点间的关系集合(Edge)组成的一种数据结构
Graph=(V,E)

无向边
1.顶点x和y之间的边没有方向,则称该边为 无向边
2.(x,y)与(y,x)意义相同,表示x和y之间有连接
本文福利,莬费领取Qt开发学习资料包、技术视频,内容包括(C++语言基础,Qt编程入门,QT信号与槽机制,QT界面开发-图像绘制,QT网络,QT数据库编程,QT项目实战,QSS,OpenCV,Quick模块,面试题等等)↓↓↓↓↓↓见下面↓↓文章底部点击莬费领取↓↓
无向图
图中任意两个顶点之间的边均是无向边,则称该图为无向图
有向边
1.顶点x和y之间的边有方向,则称该边为有向边
2.<x,y>与<y,x>意义不同,前项表示从x连接到y,后项表示从y连接到x
有向图
图中任意两个顶点之间的边钧是有向边,则称该图为有向图
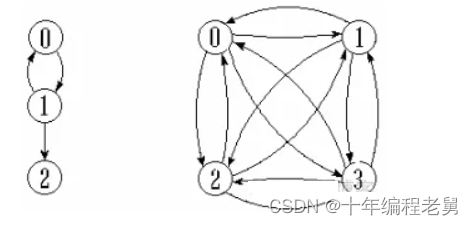
顶点邻接的定义
1.无向图–如果(x,y)属于E,则称x和y互为邻接
2.有向图–如果<x,y>属于E,则称顶点x邻接到顶点y
度(Degree)的定义
1.顶点v的度是和v相关联的边的数目,记为TD(v)
a.入度:以v为头的边的数目,记为ID(v)
b.出度:以v为尾的边的数目,记为OD(v)
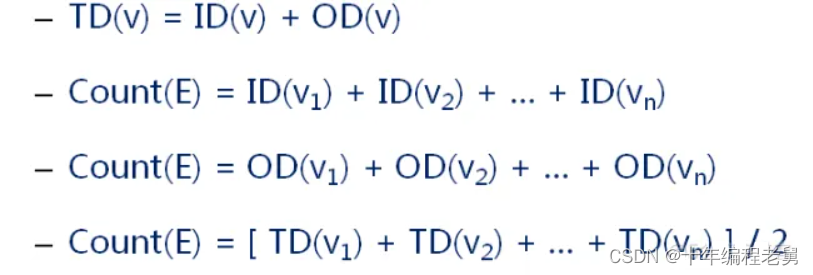
权(Weight)的定义
1.与图的边相关的数据元素叫权
2.权常用来表示图中顶点间的距离或者耗费
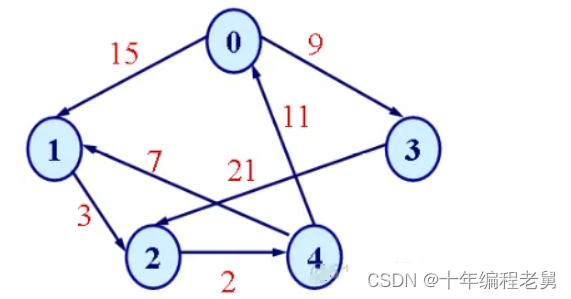
图的一些常用操作
1.设置顶点的值 2.获取顶点的值 3.获取邻接顶点 4.设置边的值
5.删除边 6.获取顶点数 等等
template <typename V,typename E>
class Graph:public Object
{
public:
virtual V getVertex(int x)=0;
virtual bool getVertex(int x,V& value)=0;
virtual bool setVertex(int i,const V& value)=0;
virtual SharedPointer<Array<int>>getAdjacent(int i)=0;
virtual E getEdge(int i,int j)=0;
virtual bool getEdge(int i, int j,E& value)=0;
virtual bool setEdge(int i, int j,const E& value)=0;
virtual bool removeEdge(int i,int j)=0;
virtual int vCount()=0;
virtual int eCount()=0;
virtual int OD(int i)=0;
virtual int ID(int i)=0;
virtual int TD(int i);
};2、图的存储结构
基本思想
1.用一维数组存储顶点:描述顶点相关的数据
2.用二维数组存储边:描述顶点间的关系和权
邻接矩阵法
-设图A=(V,E)是一个有n个顶点的图,图的邻接矩阵为Edge[n][n],则

实现方法一:直接使用数组表示顶点集和边集
template <int N,typename V,typename E>
class MatrixGraph:public Graph<V,E>
{
protected:
V m_vertexes[N];
E m_edges[N][N];
int m_eCount;
public:
//......
};问题:
1.构造效率低下–图对象初始化时,频繁调用顶点类型和边类型的构造函数
2.空间使用率低下–图对象占用大量空间,而大多数空间处于闲置状态
3.无法表示空值–无法用统一的方式表示为空的情形
实现方式二:使用指针数组表示顶点集和边集
template <int N,typename V,typename E>
class MatrixGraph:public Graph<V,E>
{
protected:
V* m_vertexes[N];
E* m_edges[N][N];
int m_eCount;
public:
//......
};问题的解决:
1.构造效率–初始化图像时,只需要将数组元素赋值为空
2.空间使用率–顶点数据元素和边数据元素在需要时动态创建
3.空值的表示–任意的顶点类型和边类型都使用NULL表示空值
图的遍历
1.广度优先–以二叉树层次遍历的思想对图进行遍历
2.深度优先–以二叉树先序遍历的思想对图进行遍历
A.广度优先算法
-原料:队列 LinkQueue<T>
-步骤
1.将起始顶点压入队列中
2.队头顶点v弹出,判断是否已经标记
3.标记顶点v,并将顶点v的邻接顶点压入队列中
4.判断队列是否为空
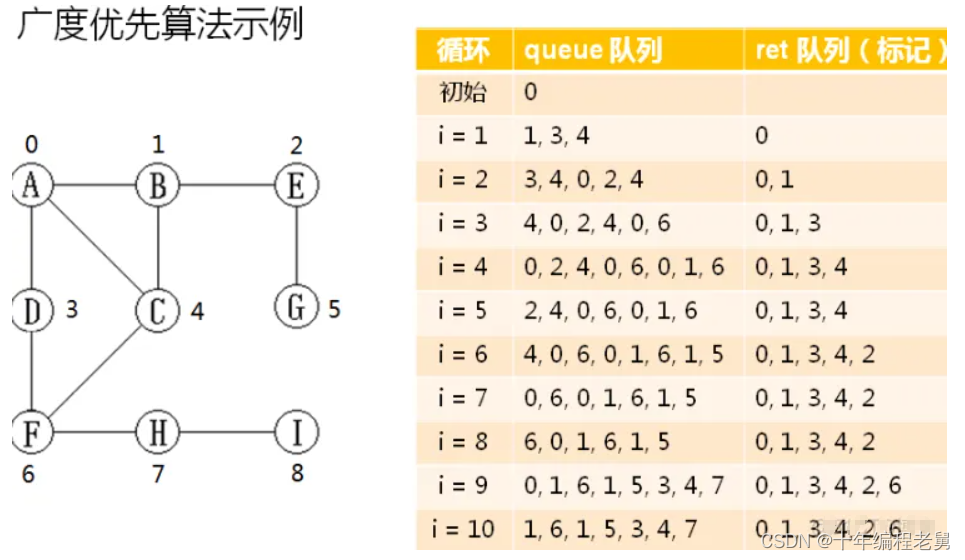
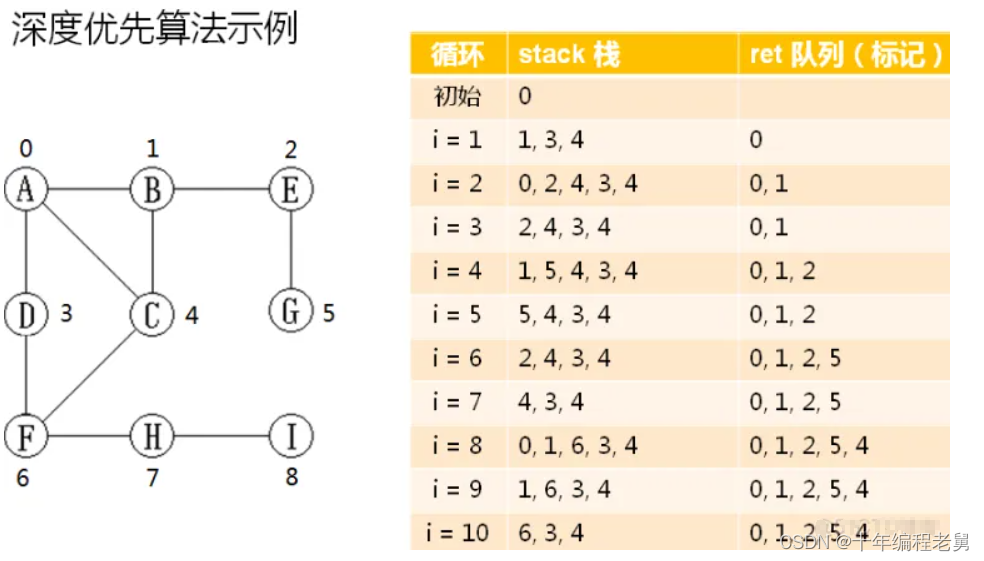
B.深度优先算法
-原料:class LinkStack<T>;
-步骤:
1.将起始点压入栈中
2.弹出栈顶顶点v,判断是否已经标记
3.标记顶点v,并将顶点v的邻接顶点压入栈中
4.判断栈是否为空
代码实现
SharedPointer<Array<int>>BFS(int i) { DynamicArray<int>* ret=NULL; if((0<=i)&&(i<vCount())) { LinkQueue<int>q; LinkQueue<int>r; DynamicArray<bool>visited(vCount()); for(int i=0;i<visited.length();i++) { visited[i]=false; } q.add(i); while(q.length()>0) { int v=q.front(); q.remove(); if(!visited[v]) { SharedPointer< Array<int> >aj=getAdjacent(v); for(int j=0;j<aj->length();j++) { q.add((*aj)[j]); } r.add(v); visited[v]=true; } } ret=toArray(r); } else { THROW_EXCEPTION(InvalidParameterException,"0.0"); } return ret; } SharedPointer<Array<int>>DFS(int i) { DynamicArray<int>* ret=NULL; if((0<=i)&&(i<vCount())) { LinkStack<int>s; LinkQueue<int>r; DynamicArray<bool>visited(vCount()); for(int j=0;j<visited.length();j++) { visited[j]=false; } s.push(i); while(s.size()>0) { int v=s.top(); s.pop(); if(!visited[v]) { SharedPointer<Array<int>>aj=getAdjacent(v); for(int j=aj->length()-1;j>=0;j--) { s.push((*aj)[j]); } r.add(v); visited[v]=true; } } ret=toArray(r); } else { THROW_EXCEPTION(InvalidParameterException,"..."); } return ret; }
本文福利,莬费领取Qt开发学习资料包、技术视频,内容包括(C++语言基础,Qt编程入门,QT信号与槽机制,QT界面开发-图像绘制,QT网络,QT数据库编程,QT项目实战,QSS,OpenCV,Quick模块,面试题等等)↓↓↓↓↓↓见下面↓↓文章底部点击莬费领取↓↓