💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学,什么是电的时候,不要觉得这些问题搞笑。哲学是科学之母,哲学就是追究终极问题,寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能让人胸中升起一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它居然给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
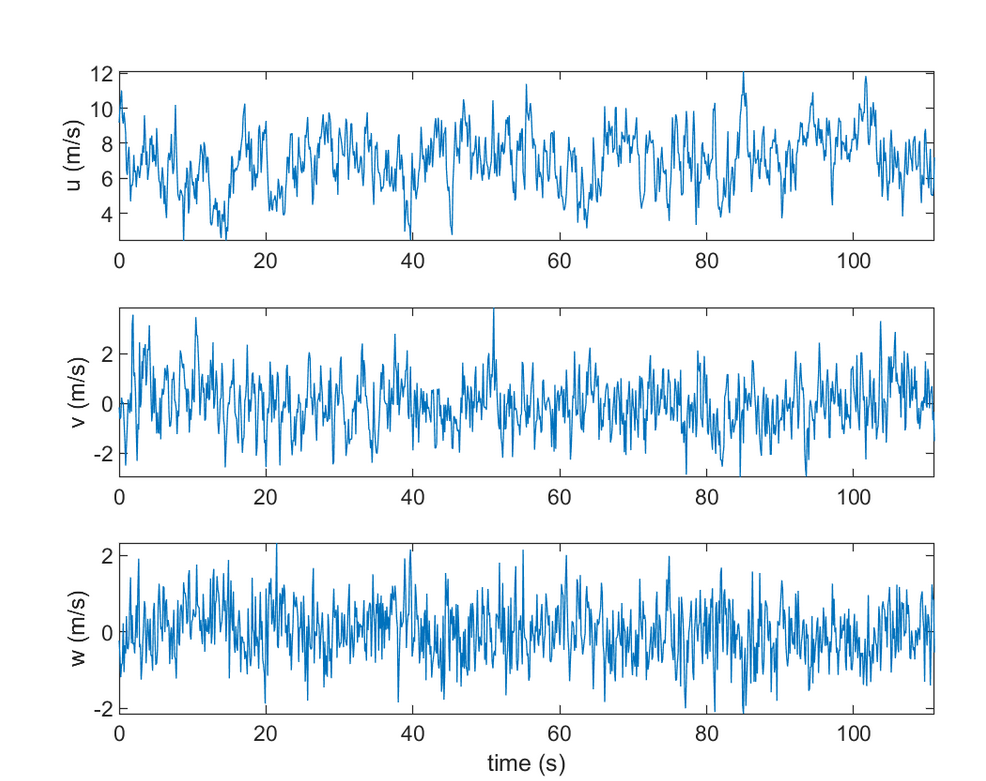
风场模拟,在三维空间中模拟一个三元空间相关的湍流风场。
摘要: 一个三维湍流风场(u、v、w 三个分量)在 3-D 中(空间两个维度,时间一个维度)使用随机过程进行模拟。模拟的计算效率依赖于文献[1],相较于函数windSim,该方法的模拟时间显著缩短。然而,这里仅考虑垂直于流向的规则二维垂直网格的情况。
内容包括:一个示例文件算例2.1,展示了输出变量的外观。
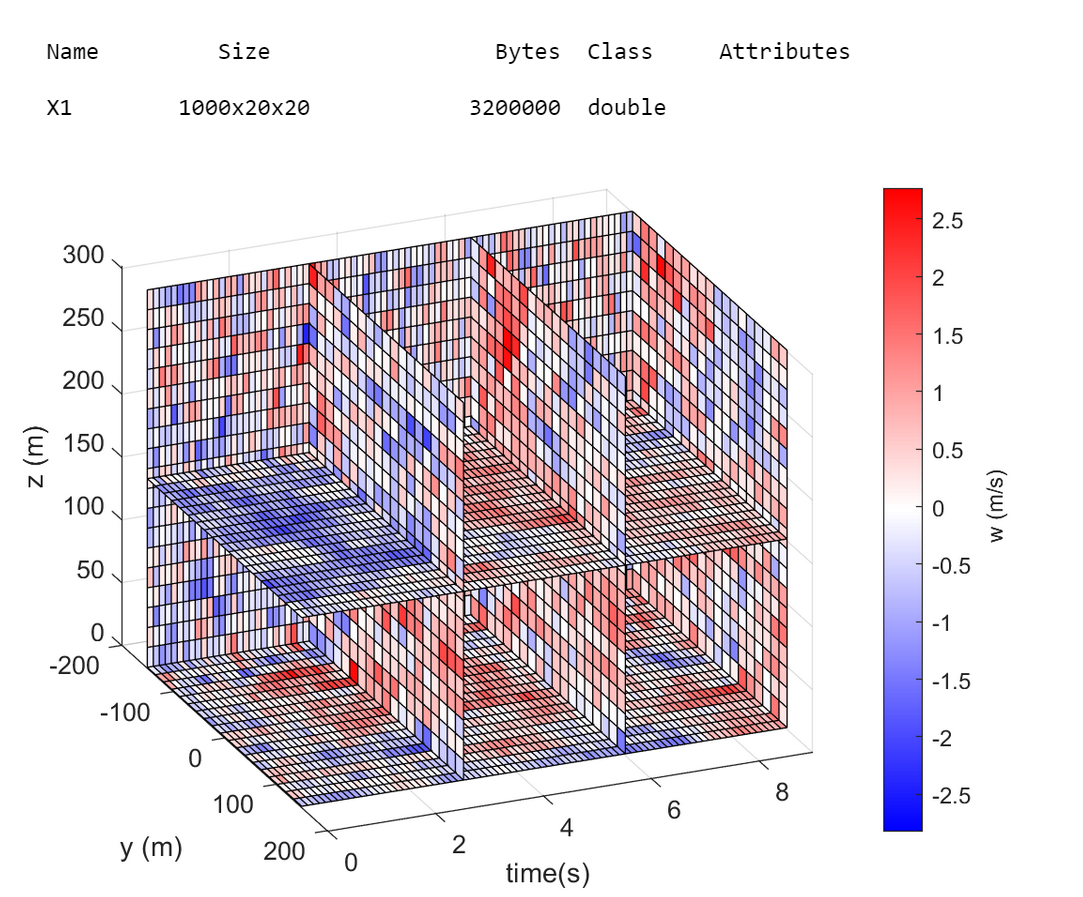
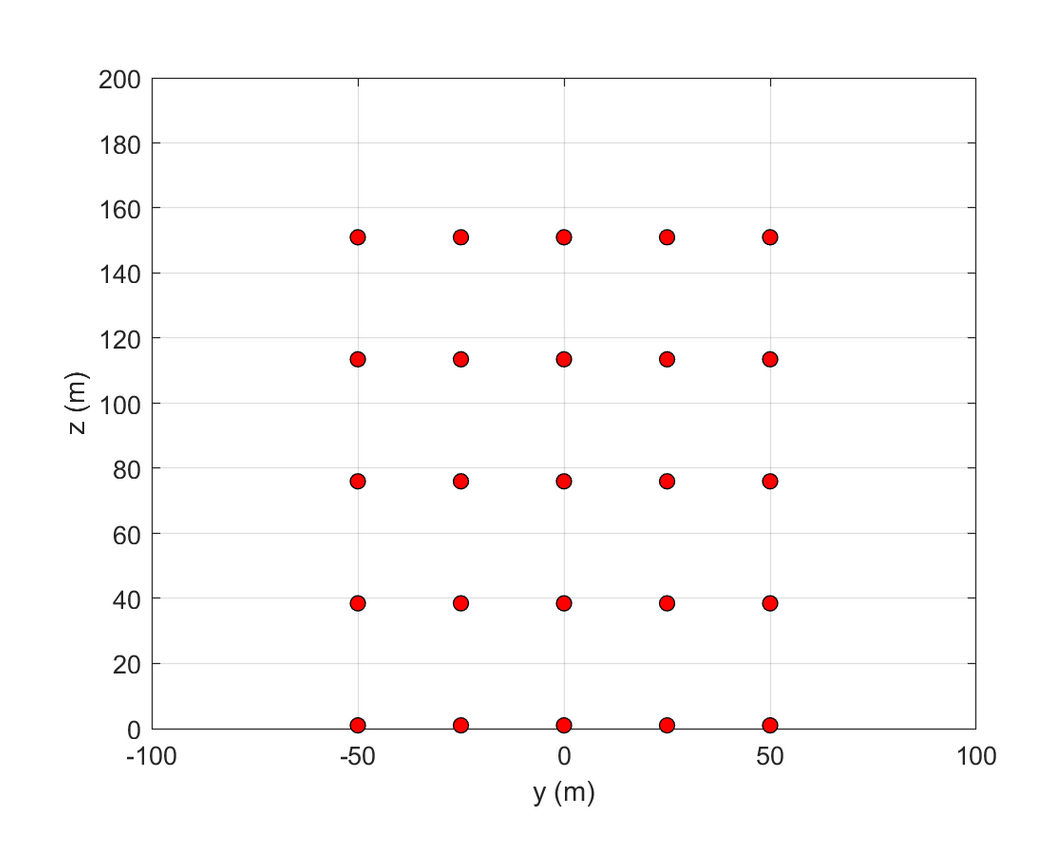
一个更完整的示例文件算例2.2,模拟了一个7x7 网格上的三维湍流风场。
在算例2.1中使用的数据文件exampleData.mat。
用于生成湍流风场的函数windSimFast.m。文献[2]中采用了类似windSimFast.m的实现。
计算时间和频率向量的函数getSamplingpara.m。
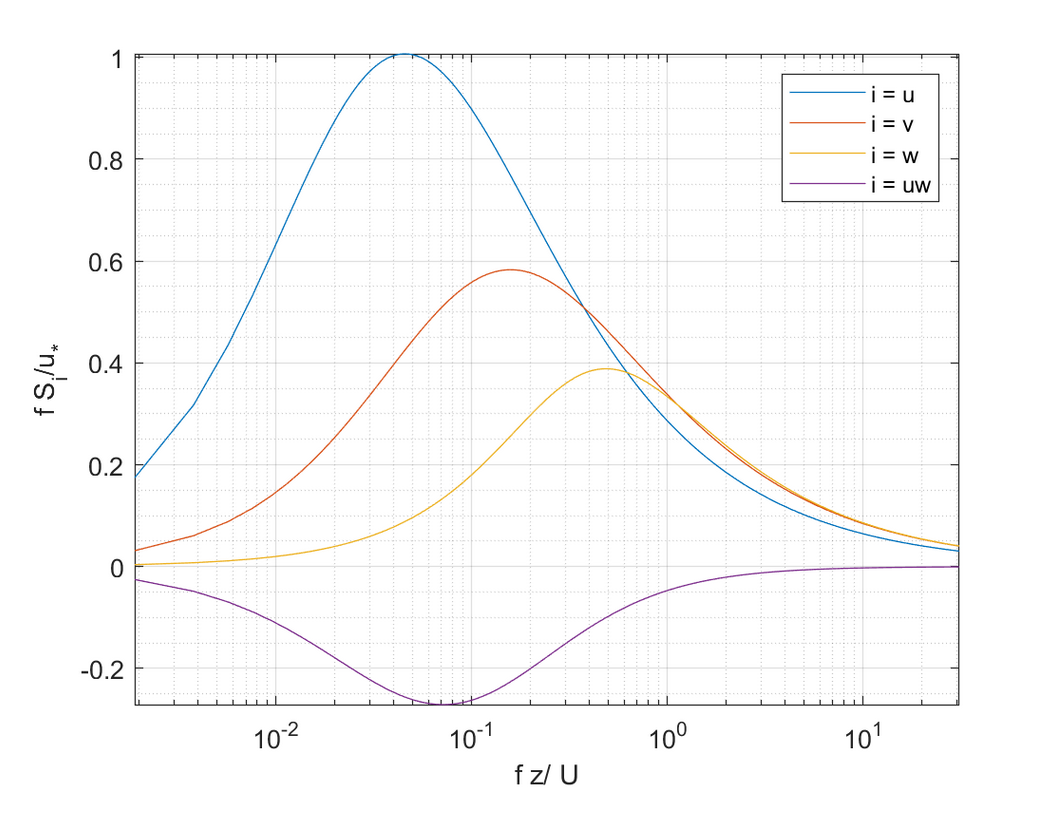
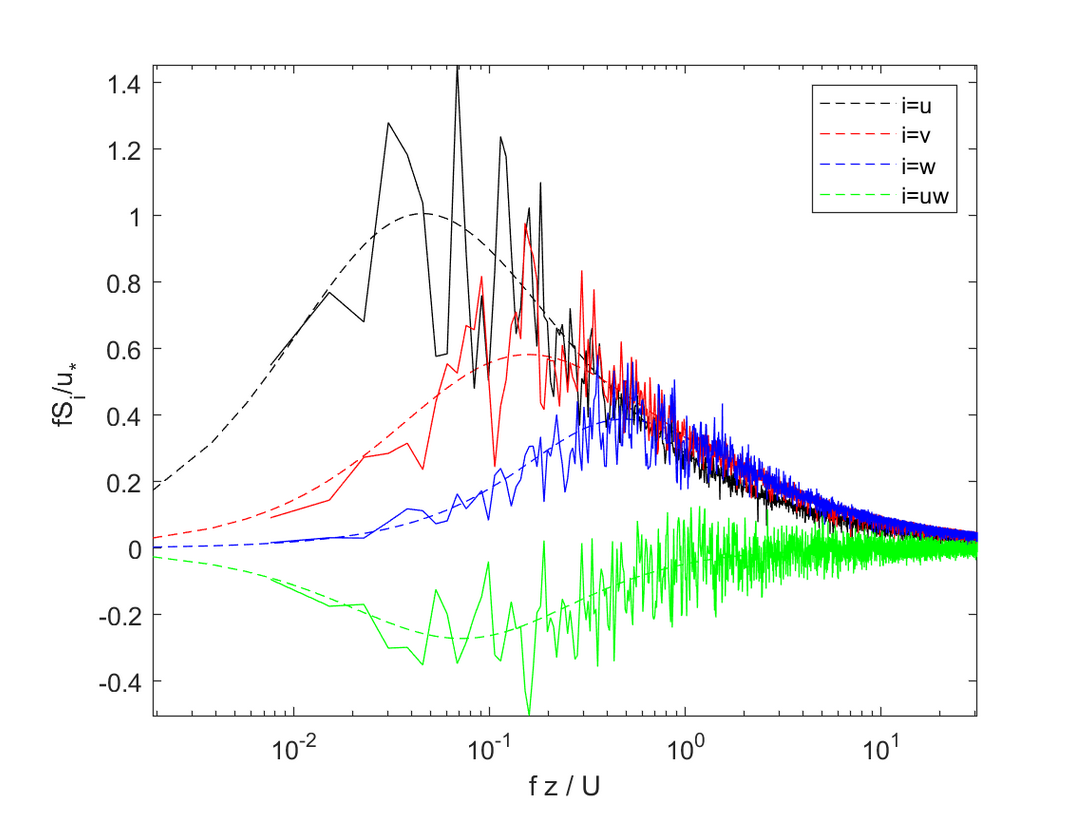
生成速度波动的单点自相关和交叉谱密度的KaimalModel.m函数,遵循Kaimal模型[3]。我已经校正了Kaimal等人使用的交叉谱密度公式,以使模拟的摩擦速度等于目标速度。
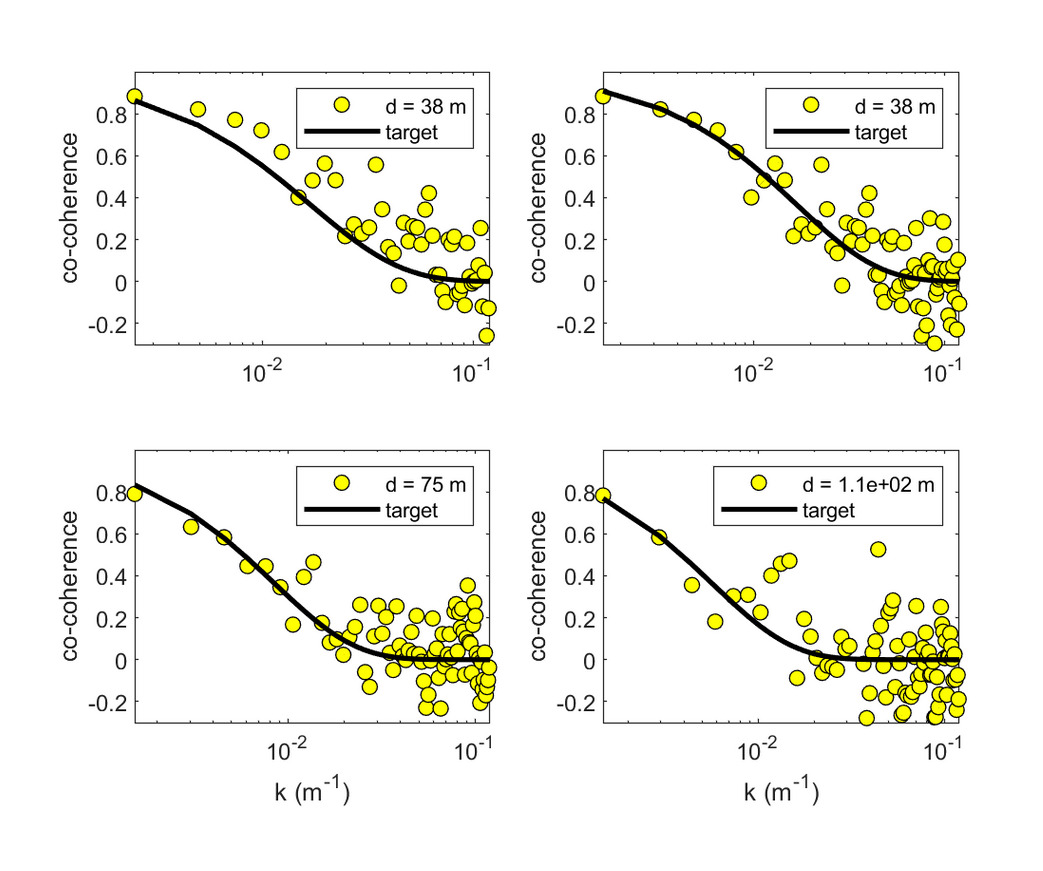
用于估算均方根相干性、相互相干性和四象限相干性的函数coherence。
将数据转换为.bts文件(二进制数据)的write2bts函数。该函数仍在测试中,我不确定它的表现如何。
风场模拟技术概述:三维空间中复杂湍流风场的高效率建模
摘要:本研究聚焦于一种创新的三维湍流风场模拟技术,该技术通过精密的随机过程在三维空间框架下(涵盖两个空间维度及一个时间维度)复现了风速分布的动态特性,具体表现为风速的三个分量u、v、w。此模拟方法在计算效率上取得了显著突破,较之经典的windSim函数,根据文献[1]的理论基础,模拟所需时间大幅度缩减。尽管目前的应用场景局限于垂直于主流向的规则二维垂直网格环境,但这一进展为后续复杂风场模拟的拓展奠定了坚实的基础。
核心内容概览:
-
算例展示:
- 算例2.1: 提供了一个直观的示范,通过展示输出变量的具体形态,使用户能够清晰理解模拟结果的结构与特征。
- 算例2.2: 进一步扩展,详尽模拟了一个更为复杂的7x7网格布局下的三维湍流风场,全面展示了模拟系统在实际应用场景中的潜力和效果。
-
关键数据与工具集:
- 数据支撑: 随附的
exampleData.mat数据文件,作为算例2.1的输入基础,确保用户可以便捷地复现研究结果,促进方法验证与学习。
- 数据支撑: 随附的
-
算法与函数实现:
windSimFast.m: 核心模拟函数,其设计灵感源自文献[2],并在原有基础上进行了优化,有效加快了模拟进程,对于大规模风场模拟具有重要价值。- 辅助函数:
getSamplingPara.m,负责计算关键的计算时间和相应的频率向量,是优化模拟频率域分析的核心工具。KaimalModel.m,遵循Kaimal模型[3]开发,用以生成速度波动的单点自相关和交叉谱密度,特别地,已修正交叉谱密度公式以保证模拟所得的摩擦速度精确匹配预设目标值,体现了对模型精度的严格把控。coherence函数套件,用于评估风场中的均方根相干性、相互相干性及四象限相干性,这些参数对于深入理解风能转换系统设计及风场特性至关重要。write2bts.m,旨在将模拟数据转换为二进制.bts格式,以便于高效存储与后续分析。当前该函数正处于测试阶段,其性能表现与兼容性有待进一步验证与优化,但仍展现了面向未来数据交换需求的前瞻性。
综上所述,本研究不仅提出了一种高效模拟三维湍流风场的新方法,还通过一系列配套工具和实例演示,全方位展现了该方法的实用性和潜在应用价值,为风能研究、城市微气候模拟以及相关领域的科学研究提供了强有力的支撑工具。
在三维空间中模拟一个与空间紧密相关的三元湍流风场是一项复杂而又重要的研究课题,对于风能利用、建筑设计、飞行器设计、大气污染扩散分析等多个领域具有深远的意义。三元湍流风场指的是风速在三个维度(水平X、Y及垂直Z轴)上同时存在随机波动和脉动,其复杂性和不确定性要求使用先进的计算模型和数值方法来进行精确的模拟。以下是一些关键研究点和方法概述:
一、引言
三维湍流风场的模拟是风能开发、航空航天及建筑风荷载分析等领域的关键技术。其核心在于通过数学模型和数值方法复现风速在空间和时间上的动态特性,尤其是三元空间相关性(即u、v、w三个速度分量的相互关联)。研究需结合流体力学理论(如三元流理论)、湍流模型(如Kaimal或Mann模型)以及高效数值算法(如LES或RANS)。
二、理论基础
1. 三元流理论
三元流理论定义流动参数为三个空间坐标(如圆柱坐标系R、φ、Z)的函数,广泛应用于叶轮机械设计。例如:
- 叶轮内流场建模:通过离散化三元空间,建立流体质点的速度分布模型,优化叶片形状以减少水力损失。
- 湍流关联性:流速函数W = f(R, φ, Z)直接关联三维湍流的空间相关性,为风场模拟提供数学框架。
2. 湍流基本特性
- 能量级串与耗散:大尺度涡通过非线性相互作用将能量传递给小尺度涡,最终通过粘性耗散。
- 相干性与非平衡态:纵向相干性描述不同位置风速的关联程度,而风演变(Wind Evolution)模型需考虑涡旋衰减和横向扩散。
三、三维湍流模拟方法
1. 物理模型选择
- Kaimal模型:基于经验谱函数,适用于大气边界层模拟,其单点自谱和交叉谱密度可描述湍流能量分布。
- Mann模型:结合谱张量与快速失真理论,通过3D逆快速傅里叶变换(FFT)生成风场,计算效率高且物理意义明确。
- Dryden模型:利用高斯白噪声滤波生成湍流信号,适合无人机等动态系统的实时模拟。
2. 数值方法对比
| 方法 | 原理 | 适用场景 | 局限性 |
|---|---|---|---|
| RANS | 雷诺平均简化方程,计算平均流动特性 | 工程快速计算 | 无法捕捉脉动细节 |
| LES | 显式求解大尺度涡,次网格模型模拟小尺度涡 | 高精度风场模拟 | 计算资源需求高 |
| DNS | 直接求解所有尺度涡 | 理论研究 | 仅适用于低雷诺数 |
3. 关键参数设置
- 湍流强度:与地表粗糙度和高度相关,需结合IEC 61400-1标准设定。
- 积分长度尺度:反映涡旋平均尺寸,影响能量谱分布。
- 相干性模型:指数衰减或概率模型量化空间关联,如Simley-Pao修正模型。
四、实施步骤与工具
1. 网格与边界条件
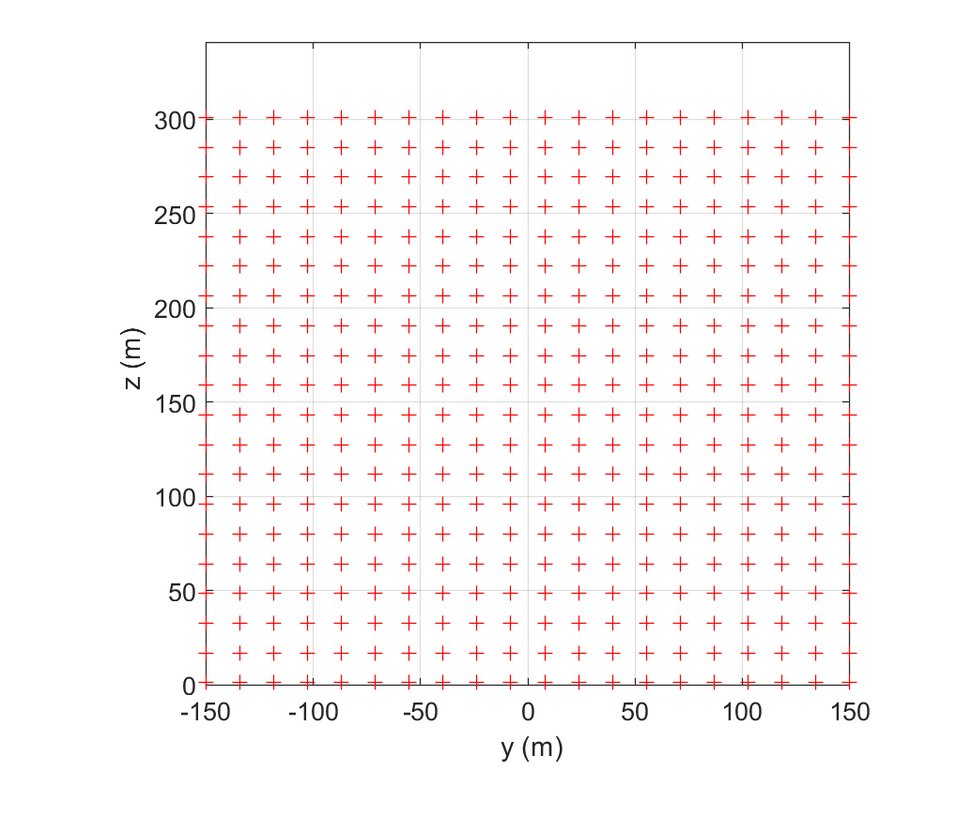
- 网格生成:垂直方向采用规则二维网格(如7×7网格),水平方向扩展为三维域。
- 粗糙度处理:通过阻力源项或亚格子模型(LES)模拟地表效应。
2. 算法实现
- 随机过程生成:Matlab工具(如
windSimFast.m)利用Kaimal谱生成三维风场,效率较传统方法提升显著。 - 谱张量分解:Mann模型通过两步Cholesky分解整合纵向相干性,支持多距离激光雷达测量。
3. 验证与校准
- 数据库对比:模拟结果需与全球风特性数据库(如NREL 5MW涡轮机数据)匹配。
- 实验验证:通过风洞测试或现场测量(如FAST索网结构响应)验证雨滴运动轨迹与风荷载分布。
五、软件工具与应用案例
1. 主流工具对比
| 工具 | 优势 | 应用案例 |
|---|---|---|
| OpenFOAM | 开源、支持大规模并行计算 | 潜艇绕流、叶轮机械模拟 |
| ANSYS Fluent | 用户友好、多物理场耦合 | 建筑风荷载、航空器气动分析 |
| Matlab | 灵活算法开发、快速原型验证 | 三维湍流场生成与数据分析 |
2. 典型案例
- 风能工程:NREL 5MW涡轮机在Kaimal风场中的动态响应,结合PID控制优化功率输出。
- 建筑风振:FAST索网结构在风雨耦合作用下的位移分析,雨滴竖向速度比建模提升精度。
- 无人机控制:基于Dryden模型的四旋翼飞行器湍流适应性控制。
六、挑战与未来方向
- 计算效率:高雷诺数LES需依赖超算资源(如天河二号),并行算法优化是关键。
- 模型融合:三元流理论与非平衡湍流模型(如动态三元相互作用)的结合。
- 多物理场耦合:风-雨-结构相互作用、光生物反应器中的流动-传质耦合。
七、结论
三维湍流风场模拟需综合流体力学理论、高效数值方法和工程实践经验。未来通过模型创新与计算技术突破,可进一步提升模拟精度与适用范围,为可再生能源、城市气候研究等领域提供关键技术支撑。
📚2 运行结果
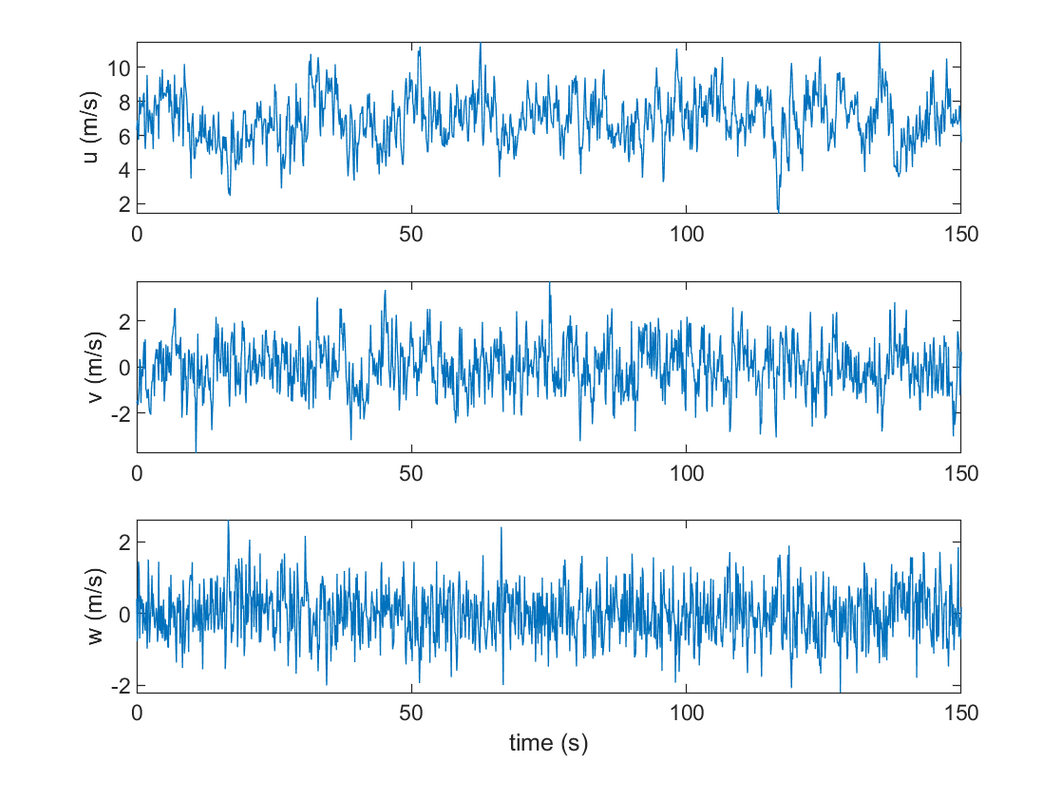
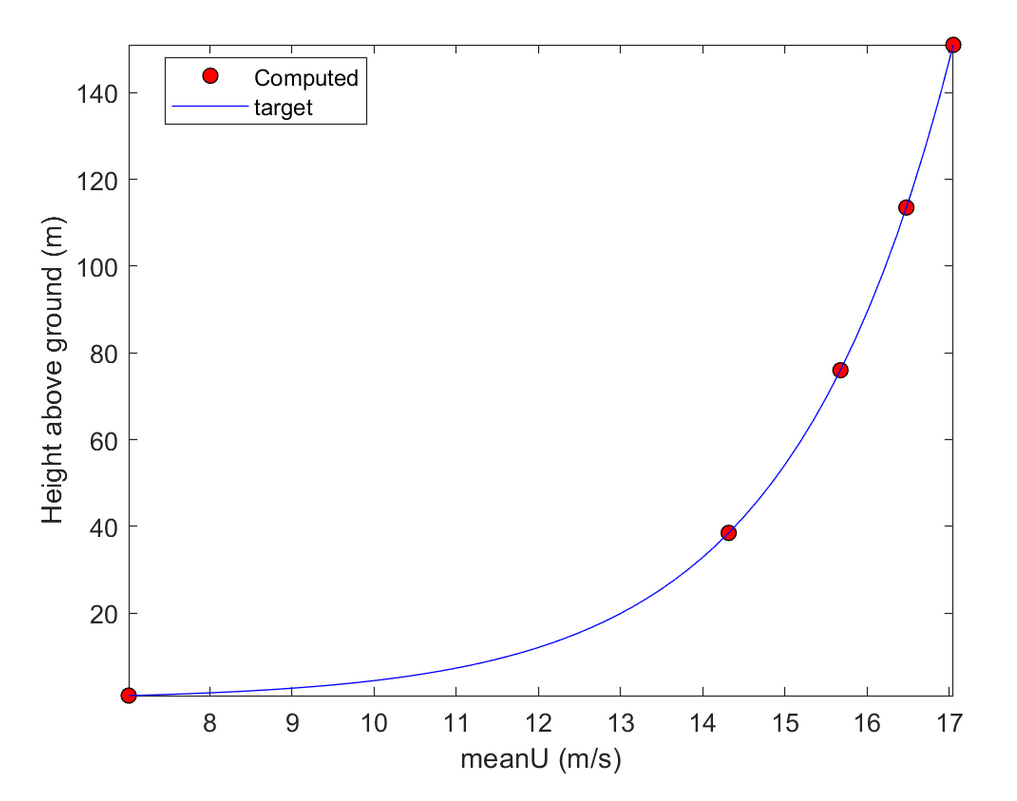
2.1 算例1
2.2 算例2
部分代码:
function [Su,Sv,Sw,Suw,Svw] = KaimalModel(U,Z,f,u_star)
% [Su,Sv,Sw,Suw,Svw] = KaimalModel(U,Z,f,u_star) computes the one-point
% auto and cross-spectral densities of the Kaimal model [1].
%
%
% Inputs:
% U: matrix [Ny x Nz] of mean wind velocity (in m/s) at each node of a grid.
% Z: matrix [Ny x Nz] of height (in m) at each node of a grid.
% f: vector [1 x Nfreq] of frequency (in Hz)
% u_star: scalar [1 x 1] friction velocity (in m/s)
%
% Outputs:
% Posing Nm = Nx*Ny and recalling that PSD = power spectral density and
% CPSD = cross-power spectral density:
% Su: vector [Nm x 1] corresponding to the PSD the u-component
% Sv: vector [Nm x 1] corresponding to the PSD the v-component.
% Sw: vector [Nm x 1] corresponding to the PSD the w-component
% Suw: vector [Nm x 1] corresponding to the CPSD the u and w components
%
% Author: E. Cheynet - UiS - last modified : 25-08-2018
%%
N = numel(f);
Nm = numel(U(:));
Su = zeros(Nm,N); % preallocation
Sv = zeros(Nm,N); % preallocation
Sw = zeros(Nm,N); % preallocation
Suw = zeros(Nm,N); % preallocation
Svw = zeros(Nm,N); % preallocation
dummyU = U(:);
dummyZ = Z(:);
for jj=1:Nm
fr = (f*dummyZ(jj)/dummyU(jj));
Su(jj,:) = 102.*fr./(1+33.*fr).^(5/3).*u_star.^2./f; % Kaimal model (NOT normalized)
Sv(jj,:) = 17.*fr./(1+9.5.*fr).^(5/3).*u_star.^2./f; % Kaimal model (NOT normalized)
Sw(jj,:) = (2.*fr./(1+5.*fr.^(5/3))).*u_star.^2./f; % Kaimal model (NOT normalized)
Suw(jj,:) = -14.*fr./(1+10.5*fr).^(7/3).*u_star.^2./f; % corrected (by me) Kaimal cross-spectrum model (NOT normalized)
end
end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1] Shinozuka, M., & Deodatis, G. (1991). Simulation of stochastic processes by spectral representation. Applied Mechanics Reviews, 44(4), 191-204.
[2] Wang, J., Cheynet, E., Snæbjörnsson, J. Þ., & Jakobsen, J. B. (2018). Coupled aerodynamic and hydrodynamic response of a long span bridge suspended from floating towers. Journal of Wind Engineering and Industrial Aerodynamics, 177, 19-31.
[3] Davenport, A. G. (1961). The spectrum of horizontal gustiness near the ground in high winds. Quarterly Journal of the Royal Meteorological Society, 87(372), 194-211.
🌈4 Matlab代码实现
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取