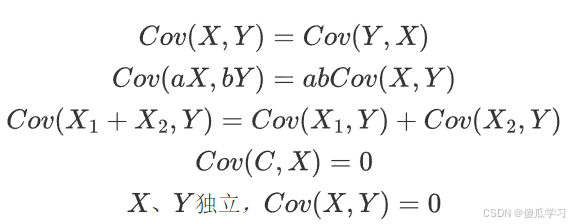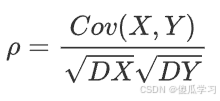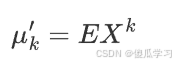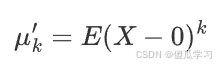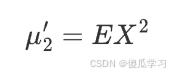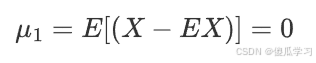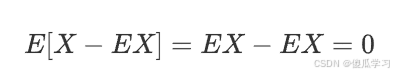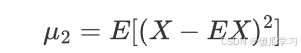数学期望
数学期望是概率论中的一个重要概念,它描述了一个随机变量的平均值或中心值。数学期望也被称为期望值或均值。它是对随机变量可能取值的加权平均,其中权重是每个可能取值的概率。
离散型随机变量的期望
1.对于离散随机变量 X ,其可能的取值为 x1,x2,…,xn,对应的概率为
,则 X 的数学期望定义为:
其中 xi是随机变量 X 的可能取值,pi是 X取值为 xi的概率。
2.例1
- 有三个人的体重分别为150、165、180,求体重的期望值。
- 解:
- 三个人体重的概率相等,都是1/3,所以期望值:
其实就是求平均体重。
3.例2
- 学校举行歌唱比赛,假设给一个参赛选手打分,专业评委打分90,老师打分100,学生打分80,专业评委分数权重为0.9,老师权重为0.09,学生权重为0.01,求给该选手的打分期望值。
- 解:
- 设随机变量X,其取值分别为打分值:90、100、80,对应的概率为打分权重:0.9、0.09、0.01
- 所以,X的期望值为:
该题其实就是加权平均值。
4.例3
- 甲乙两人X、Y生产产品,次品率分别为:
| X | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| P | 0.3 | 0.3 | 0.2 | 0.2 |
| Y | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| P | 0.2 | 0.5 | 0.3 | 0.0 |
- 求甲乙谁的次品率高。
- 解:根据期望值来计算:
- 甲:
- 乙:
所以甲的次品率高。
连续型随机变量的期望
1、对于连续随机变量 X ,其概率密度函数为 f(x) ,则 X 的数学期望定义为:
说明:
可以将x理解为随机变量X的取值,f(x)理解为对应的概率。在严格意义上不是正确的,帮助我们理解。
2.例子
- 假设概率密度函数
- 求期望值。
- 解:
随机变量函数的期望
离散型随机变量函数的期望
1.如果 X 是一个离散随机变量,其可能的取值为 x1,x2,…,xn,对应的概率为 P(X=xi)=pi,那么函数 Y=g(X) 的期望值定义为:
说明:
g(xi):X的取值xi带入函数Y=g(X)得到的新的取值。
计算逻辑:
将X的取值直接带入Y=g(X)函数得出新的取值,然后新值乘以对应的概率,将所有新取值与对应概率乘积相加即可。
2.例子
- 假设X的概率分布表:
| X | 0 | 1 | 2 |
|---|---|---|---|
| P | 0.1 | 0.6 | 0.3 |
- 函数Y=4X+1,求Y的期望。
- 解:
连续型随机变量函数的期望
1.如果 X 是一个连续随机变量,其概率密度函数为 f(x),那么函数 Y=g(X)的期望值定义为:
2.例1
- 假设密度函数
- 函数Y=4X+1,求Y的期望。
- 解:直接代入公式
二维离散型随机变量函数的期望
1.如果 (X,Y) 是离散随机变量,其取值集合为 {(xi,yj)} ,对应的概率为
,那么函数 Z=g(X,Y) 的数学期望定义为:
说明:
表示将X、Y的所有取值按照Z=g(X,Y) 计算出新的取值。
2.例2
- 假设X、Y联合概率分布表:
| X\y | 0 | 1 | 2 |
|---|---|---|---|
| 1 | 0.1 | 0.1 | 0.2 |
| 2 | 0.2 | 0.2 | 0.2 |
求
的期望。
- 解:
- 将X、Y的所有取值按照Z=g(X,Y) 计算出新的取值,乘以对应的概率,然后相加。
二维连续型随机变量函数的期望
1.如果 (X,Y) 是连续随机变量,其联合概率密度函数为 f(x,y),那么函数 Z=g(X,Y)的数学期望定义为:
这里,g(X,Y) 是 X和 Y的函数。
2.例子
- 假设X、Y的联合密度函数
求E(XY)
- 解:直接代入公式
数学期望的性质
-
常数的期望等于常数,EC=C
-
E(X+C)=EX+C
-
E(CX)=C*EX
-
E(kX+b)=k*EX+b
-
E(X±Y)=EX+EY (任何时候都成立 ) E(∑CiXi) = ∑CiEXi
-
X、Y独立,E(XY)=EX*EY
1.例子
- 假设X、Y独立,X和Y的分布表如下:
| X | 9 | 10 | 11 |
|---|---|---|---|
| P | 0.3 | 0.5 | 0.2 |
| Y | 6 | 7 |
|---|---|---|
| P | 0.4 | 0.6 |
求:
- 解:
- 先计算EX和EY:
- 使用性质5计算
- 使用性质6计算
- 两个事件Y不能确定是独立的,所以不能使用性质计算,使用定义来做
方差
1.方差是统计学中一个重要的概念,用于衡量随机变量或一组数据的离散程度。它反映了数据点与其平均值之间的偏离程度。方差越大,数据点越分散;方差越小,数据点越集中。
2.对于一个随机变量 X,其方差 Var(X)或DX定义为:
3.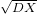
4.DX的推导
- 由E(kX+b)=k*EX+b可将DX进行展开,EX是一个常数
离散型随机变量的方差
1.对于离散型随机变量 X,其方差可以表示为:
4.例子
- 假设
| X | -2 | 0 | 2 |
|---|---|---|---|
| P | 0.4 | 0.3 | 0.3 |
- 求方差DX。
- 解:
- 先求EX:
- 再求EX^2:
- 求方差:
连续型随机变量的方差
1.对于连续型随机变量 XX,其方差可以表示为:
2.例子
- 假设密度函数:
- 求方差DX。
- 解:
- 求EX:
- 求EX^2:
- 求DX:
方差的性质
-
常数的方差:
-
-
-
X、Y独立,
-
X、Y不独立,
是协方差,后边会讲
推导
这里需要注意方差的性质与期望性质的不同。
常见离散型的期望与方差
1 0-1分布
| X | 0 | 1 |
|---|---|---|
| p | 1-p | p |
其中q=1-p
二项分布
期望与方差:
几何分布
泊松分布
常见连续型的期望与方差
均匀分布
指数分布
正态分布
期望与方差:
协方差
1.协方差是衡量两个随机变量之间线性关系强度的统计量。如果两个变量的协方差为正,它们之间存在正相关关系;如果协方差为负,它们之间存在负相关关系;如果协方差为零,它们之间没有线性关系。
2. 定义:对于两个随机变量 X 和 Y,它们的协方差定义为:
其中 EX 和 EY 分别是 X 和 Y 的期望值。
协方差的计算公式可以表示为:
推导
3. 性质
4.相关系数
- 协方差的一个限制是它的值依赖于变量的尺度。为了克服这个限制,通常使用相关系数(Pearson相关系数)来衡量两个变量之间的线性关系,其定义为:
相关系数的值在 -1 和 1 之间,其中 -1 表示完全负相关,1 表示完全正相关,0 表示没有线性关系。
解释
- 正相关:如果相关系数为正,表明当一个变量的值增加时,另一个变量的值也倾向于增加。
- 负相关:如果相关系数为负,表明当一个变量的值增加时,另一个变量的值倾向于减少。
- 无相关:如果相关系数为零,表明两个变量之间没有线性关系。
原点矩和中心距
1.中心距和原点矩分别描述了随机变量在其期望值(中心)和原点(零点)周围的分布情况。
原点矩
1.原点矩是随机变量 X与原点0的差 的幂次期望值。对于随机变量 X,其 k 阶原点矩定义为:
其中 E 表示期望值。可以理解为:
常见原点矩
1.一阶原点矩
这实际上是随机变量 X 的期望值(平均值)。
2.二阶原点矩
这实际上是随机变量 X 的平方的期望值。
中心距
1.中心距是随机变量 X 与其期望值 EX的差的幂次期望值。对于随机变量 X,其 k 阶中心距定义为:
其中 E 表示期望值。
常见中心距
1.一阶中心距
这实际上是零,因为
2.二阶中心距:
这实际上是随机变量 X 的方差 DX。
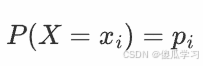
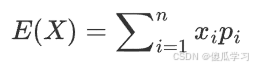
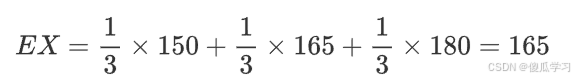
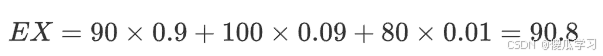
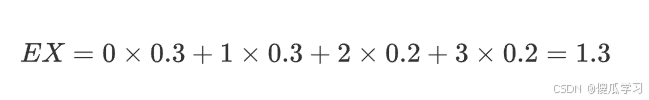
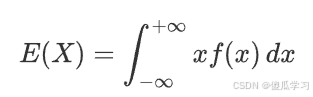
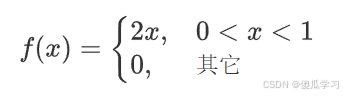
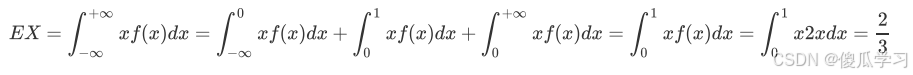
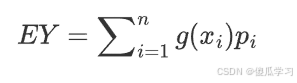
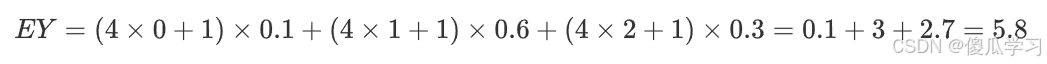
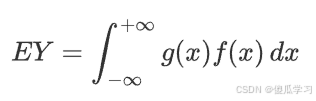

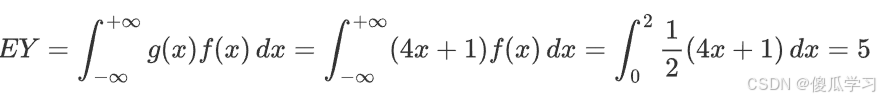
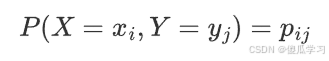
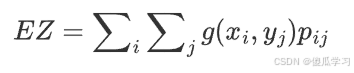
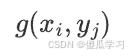
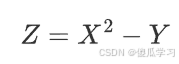
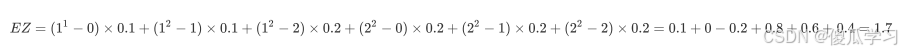
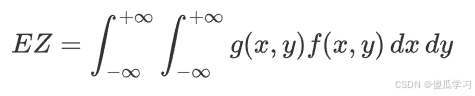

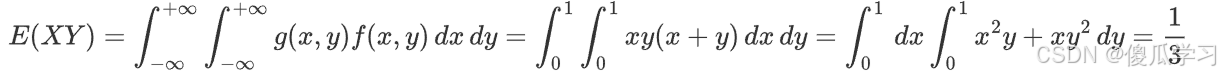
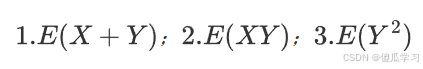
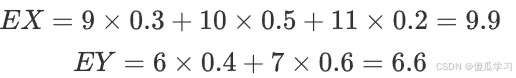
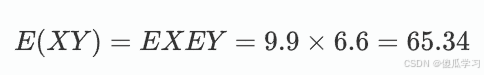
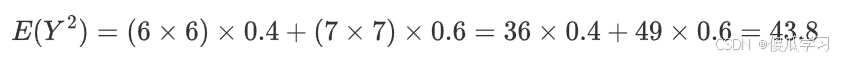

![DX=E[(X-EX)^2]=E(X^2)-2EXEX+(EX^2)=E(X^2)-(EX)^2](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8%3DDX%3DE%5B%28X-EX%29%5E2%5D%3DE%28X%5E2%29-2EXEX+%28EX%5E2%29%3DE%28X%5E2%29-%28EX%29%5E2)

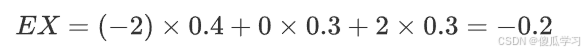
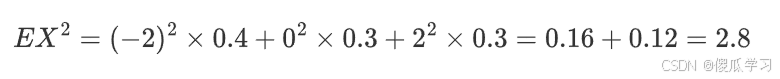
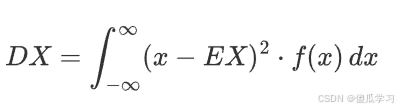

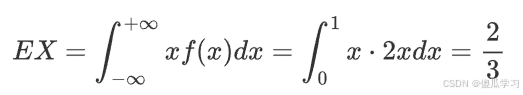
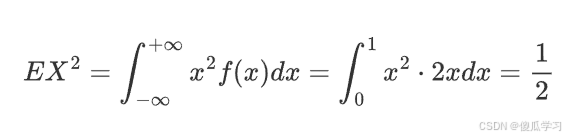
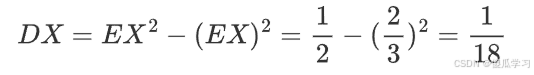
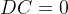

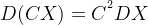


![D(X\pm Y)=E[(X \pm Y)-E(X \pm Y)]^2=E[(X\pm Y)-(EX \pm EY)]^2=E[(X-EX) \pm (Y-EY)]^2=E[(X-EX)^2+(Y-EY)^2 \pm 2(X-EX)(Y-EY)]=E(X-EX)^2+E(Y-EY)^2 \pm 2E[(X-EX)(Y-EY)]=DX^2+DY^2 \pm 2COV(X,Y)](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8%3DD%28X%5Cpm%20Y%29%3DE%5B%28X%20%5Cpm%20Y%29-E%28X%20%5Cpm%20Y%29%5D%5E2%3DE%5B%28X%5Cpm%20Y%29-%28EX%20%5Cpm%20EY%29%5D%5E2%3DE%5B%28X-EX%29%20%5Cpm%20%28Y-EY%29%5D%5E2%3DE%5B%28X-EX%29%5E2+%28Y-EY%29%5E2%20%5Cpm%202%28X-EX%29%28Y-EY%29%5D%3DE%28X-EX%29%5E2+E%28Y-EY%29%5E2%20%5Cpm%202E%5B%28X-EX%29%28Y-EY%29%5D%3DDX%5E2+DY%5E2%20%5Cpm%202COV%28X%2CY%29)
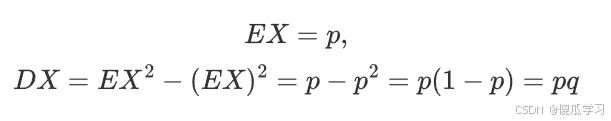
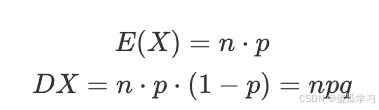
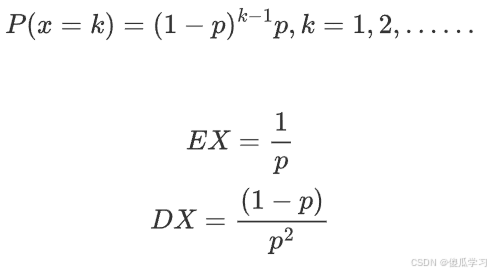
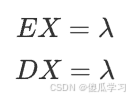
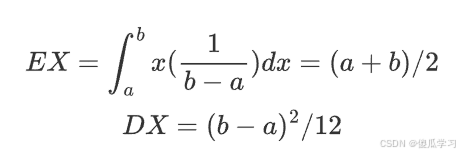
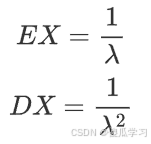
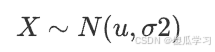
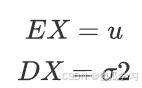
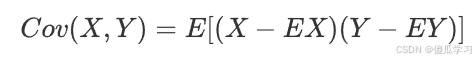
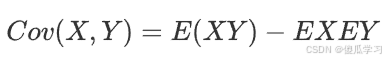

![Cov(x,y)=E[(X-EX)(Y-EY)]=E(XY-XEY-YEX+EXEY)=E(XY)-EXEY-EYEX+EXEY=E(XY)-EXEY](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8%3DCov%28x%2Cy%29%3DE%5B%28X-EX%29%28Y-EY%29%5D%3DE%28XY-XEY-YEX+EXEY%29%3DE%28XY%29-EXEY-EYEX+EXEY%3DE%28XY%29-EXEY)