101 对称二叉树

我比较喜欢用迭代的方法来做题目 因为有的用递归法真的理解不了 这道题用迭代的方法思路很清晰 首先就是判断根节点 判断结束后 用层序遍历的方式 用一个队列que 放入根节点的左右孩子 然后开始进入while当队列里面不为空的时候 用两个临时的节点 接受队列出口的两个节点（即左孩子和右孩子）if判断 当左右孩子都为空 则continue 若左右孩子有一个为空 或者都不为空但是左右孩子的值不相等 返回false 最后按顺序加入左节点的左孩子 右节点的右孩子 左节点的右孩子 右节点的左孩子

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(root==nullptr) return true;
        queue<TreeNode*> que;
        que.push(root->left);
        que.push(root->right);
        while(!que.empty()){
            TreeNode* leftnode = que.front();
            que.pop();
            TreeNode* rightnode = que.front();
            que.pop();
            if(!leftnode && !rightnode){
                continue;
            }
            if(!leftnode||!rightnode||(leftnode->val!=rightnode->val)){
                return false;
            }
            que.push(leftnode->left);
            que.push(rightnode->right);
            que.push(leftnode->right);
            que.push(rightnode->left);
        }
        return true;
    }   
};

 二叉树的最大深度

主要在这里写一下递归的方法（迭代法用层序遍历可以很容易写出来）递归的三步 1.确定递归函数的参数和返回值 返回int 传入的是节点 然后判断终止条件 当该节点是空 返回0；然后分别计算左子树的深度 右子树的深度 最后取左右子树的最大值加上1 得到二叉树的最大深度

class Solution {
public:
    int getdepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftdepth = getdepth(node->left);       // 左
        int rightdepth = getdepth(node->right);     // 右
        int depth = 1 + max(leftdepth, rightdepth); // 中
        return depth;
    }
    int maxDepth(TreeNode* root) {
        return getdepth(root);
    }
};

  二叉树的最小深度

主要写一下递归的方法 同样是节点为空 return 0；然后分别计算左右子树的深度 然后当一个左子树的左右孩子有一个不为空 分两个情况 左子树为空时 返回的时右子树的深度+1 若右子树为空 则返回左子树的深度+1 最小的深度就是左右子树的深度取最小值加上1

class Solution {
public:
    int getDepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftDepth = getDepth(node->left);           // 左
        int rightDepth = getDepth(node->right);         // 右
                                                        // 中
        // 当一个左子树为空，右不为空，这时并不是最低点
        if (node->left == NULL && node->right != NULL) { 
            return 1 + rightDepth;
        }   
        // 当一个右子树为空，左不为空，这时并不是最低点
        if (node->left != NULL && node->right == NULL) { 
            return 1 + leftDepth;
        }
        int result = 1 + min(leftDepth, rightDepth);
        return result;
    }

    int minDepth(TreeNode* root) {
        return getDepth(root);
    }
};

求深度的类型 都是用后序遍历 从孩子节点开始 一步一步往上计算深度 

110 平衡二叉树 判断是否是平衡二叉树

平衡二叉树时一个节点的左右子树的高度差不能超过1 遇到高度差也是两个子树的深度差 求深度用后序遍历 同样先判断节点若为空 返回0 然后分别计算左右孩子的深度 如果左孩子为空 返回-1 右孩子为空返回-1 然后最后返回判断左右孩子的深度差是否大于1 如果大于1 则返回-1 如果不是就返回左右子树中最大的深度+1

class Solution {
public:
    int getHeight(TreeNode* node){
        if(node == nullptr) return 0;
        int leftheight = getHeight(node->left);
        int rightheight = getHeight(node->right);
        
        if(leftheight==-1){
            return -1;
        }
        if(rightheight==-1){
            return -1;
        }
        return abs(leftheight-rightheight) > 1 ? -1 : 1 + max(leftheight,rightheight);
    }
    bool isBalanced(TreeNode* root) {
        return getHeight(root) == -1 ? false : true;
    }
};

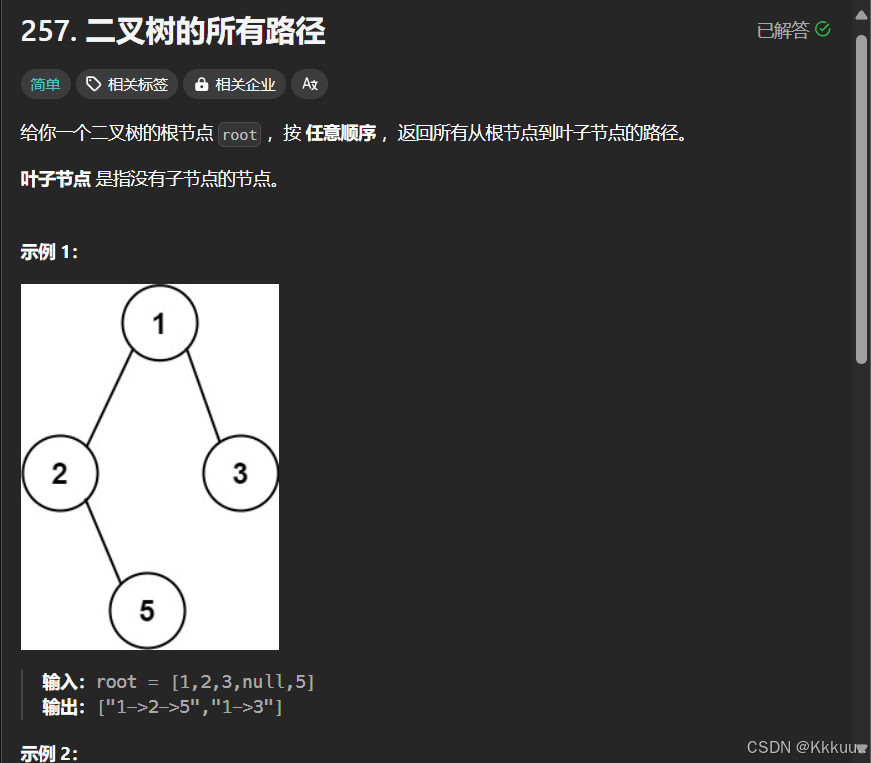
257 二叉树的所有路径

这题需要用到回溯的思想 这个题目递归函数的参数要有一个节点 一个数组来接收路径 另一个数组接收答案 首先需要先让节点放入路径数组 因为如果先判断该节点是否是叶子的节点的话 如果是叶子节点 就要处理路径数组了 最后的叶子节点就放不进数组了 所以先把节点放入路径数组 然后判断该节点是否是叶子节点 如果不是 就再判断 该节点的左孩子是否为空 如果不为空 就递归左孩子 但是要回溯 路径数组要弹出元素 右孩子也是同样操作 （这个回溯代码就如下图相当于 一直往左孩子遍历直到节点为空后 返回出来 然后要弹出放入节点的左孩子 才能回到原来的父节点 进入下面的右孩子的遍历）

class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& path, vector<string>& ans){
        path.push_back(cur->val);
        if(cur->left==nullptr && cur->right==nullptr){
            string spath;
            for(int i=0;i<path.size()-1;i++){
                spath+= to_string(path[i]);
                spath+="->";
            }
            spath+=to_string(path[path.size()-1]);
            ans.push_back(spath);
            return;
        }

        if(cur->left){
            traversal(cur->left,path,ans);
            path.pop_back();
        }
        if(cur->right){
            traversal(cur->right,path,ans);
            path.pop_back();
        }
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        vector<int> path;
        vector<string> ans;
        if(root==nullptr) return ans;
        traversal(root,path,ans);
        return ans;
    }
};

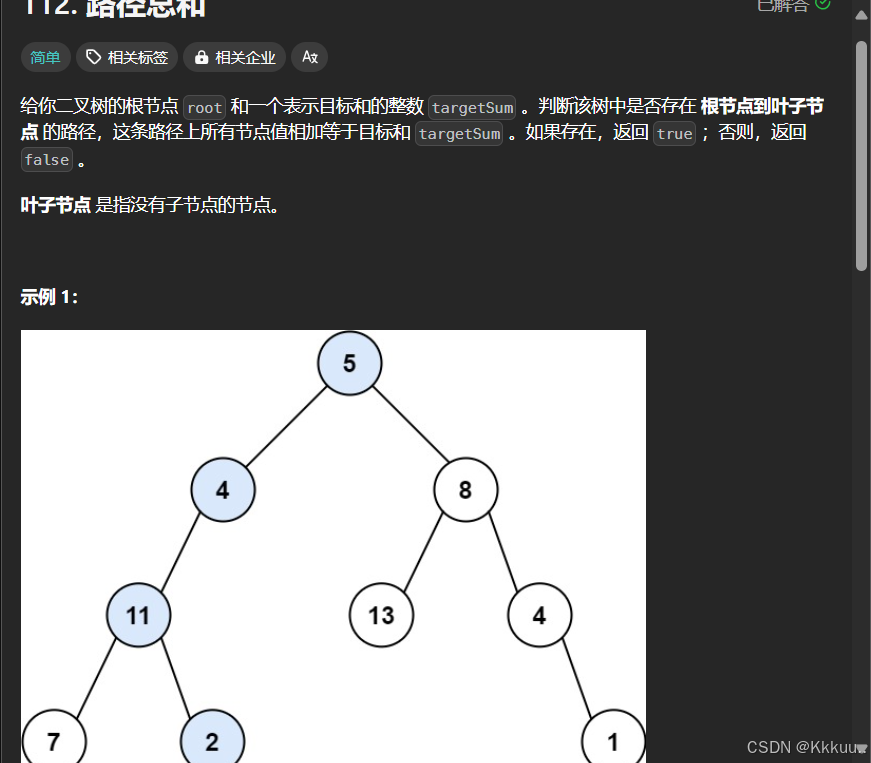
 112 路径总和

这道题和求路径很像 都是需要回溯的 我们这一题 在原函数判断根节点的情况 然后return 递归函数的时候 把参数设为目标值减去根节点的值 然后写递归函数的参数需要一个节点 一个count值 判断根的左右孩子如果为空 并且传进来的值为0 就代表这个路径就是根节点 若值不为0 返回false；接下来就是如果左孩子不为空 则向左孩子遍历 然后递归count减去左孩子的值 回溯就是再加回来这个值 右孩子也是同样的逻辑 最后如果在之前没有返回true则在最后返回false

class Solution {
public:
    bool traversal(TreeNode* cur, int count){
        if(!cur->left && !cur->right && count==0){
            return true;
        }
        if(!cur->left && !cur->right) return false;

        if(cur->left){
            count-=cur->left->val;
            if(traversal(cur->left,count)) return true;
            count+=cur->left->val;
        }
        if (cur->right) { 
            count -= cur->right->val; 
            if (traversal(cur->right, count)) return true;
            count += cur->right->val;
        }
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==nullptr) return false; 
        return traversal(root,targetSum-root->val);
    }
};

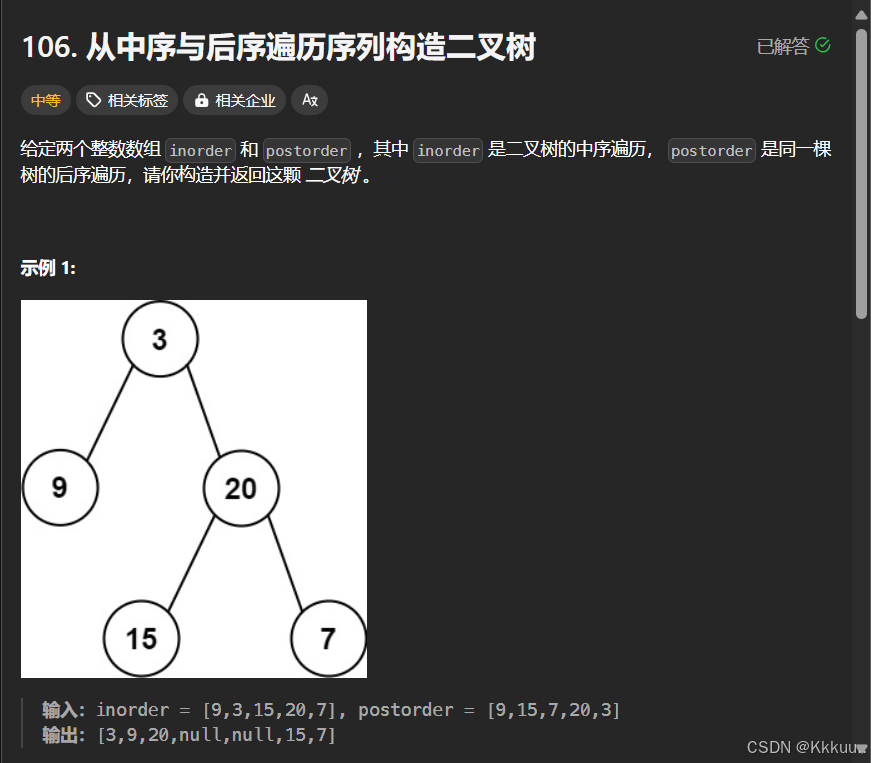
 106 从中序后序遍历序列构造二叉树

这题思路其实很清晰 但是代码写起来很多问题 写一个遍历的递归函数 参数是两个遍历数组 判断终止条件 就是后序的数组如果为空了 return nullptr 然后后序遍历数组的最后一个值 就是根节点的值 用一个节点接收（如果后序数组就1个值 就直接return root）然后就开始在中序遍历数组找到这个根节点 用两个vector容器在中序遍历数组确定左子树和右子树的区间 确定之后 在后序遍历数组删除最后的根节点 然后再用两个vector容器在后序遍历数组确定左右子树的区间 让接收根节点的临时节点的左孩子用得到的两个左子树区间递归 右孩子也是同样逻辑

class Solution {
public:
    TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {
        if(postorder.size()==0) return nullptr;

        int rootvalue = postorder[postorder.size()-1];
        TreeNode* root = new TreeNode(rootvalue);
        if(postorder.size()==1) return root;
        
        int index;
        for(index=0;index<inorder.size();index++){
            if(inorder[index]==rootvalue){
                break;
            }
        }

        vector<int> leftinorder(inorder.begin(),inorder.begin()+index);
        vector<int> rightinorder(inorder.begin()+index+1,inorder.end());

        postorder.resize(postorder.size()-1);

        vector<int> leftpostorder(postorder.begin(),postorder.begin()+leftinorder.size());
        vector<int> rightpostorder(postorder.begin()+leftinorder.size(),postorder.end());

        root->left = traversal(leftinorder,leftpostorder);
        root->right = traversal(rightinorder,rightpostorder);
        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size()==0 || postorder.size()==0) return nullptr;
        return traversal(inorder,postorder);
    }
};

 105 从中序前序遍历序列构造二叉树 

和上一个题目的逻辑其实是一样的 但是递归函数的参数 需要两个数组 以及两个数组的开始位置和终止位置（我认为是vector不好删除第一个根节点的元素 后序递归的时候 不好处理 我尝试用过106类似的代码 一直有错误 不知道是不是我哪里写错了） 其余逻辑都是一样的 要主要前序遍历数组的根节点是该数组的第一个元素 

class Solution {
public:
    TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
        if (preorderBegin == preorderEnd) return NULL;

        int rootvalue = preorder[preorderBegin];
        TreeNode* root = new TreeNode(rootvalue);
        if(preorderEnd-preorderBegin==1) return root;

        int index;
        for(index=inorderBegin;index<inorderEnd;index++){
            if(inorder[index]==rootvalue){
                break;
            }
        }

        int leftinorderbegin = inorderBegin;
        int leftinorderend = index;
        int rightinorderbegin = index+1;
        int rightinorderend = inorderEnd;

        int leftpreorderbegin = preorderBegin+1;
        int leftpreorderend = preorderBegin+1+index-inorderBegin;
        int rightpreorderbegin = preorderBegin+1+index-inorderBegin;
        int rightpreorderend = preorderEnd;

        root->left = traversal(inorder, leftinorderbegin, leftinorderend,  preorder, leftpreorderbegin, leftpreorderend);
        root->right = traversal(inorder, rightinorderbegin, rightinorderend, preorder, rightpreorderbegin, rightpreorderend);

        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0 || inorder.size()==0){
            return nullptr;
        }
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
    }
};

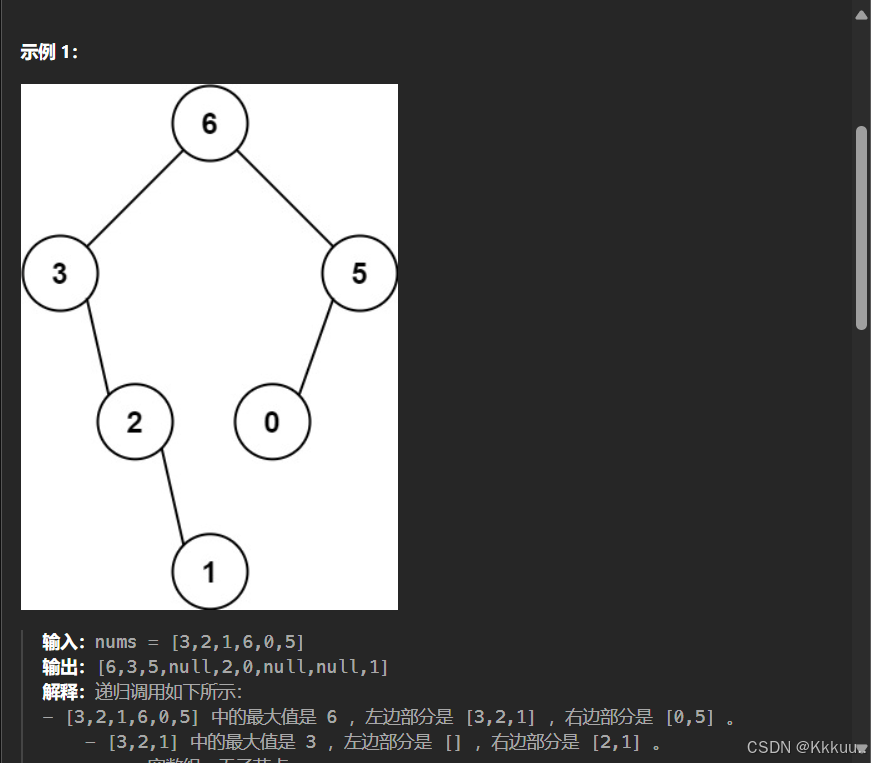
654 最大的二叉树 

本题的思路和前两个题目也很像 判断数组只有一个元素的情况 就直接返回根节点 然后用两个int变量通过循环记录最大值以及它的下标 如果下标>0 不是第一个元素 用一个数组把该元素左边的区间收集起来 作为左子树进入递归函数 如果下标<数组长度-1 即不是最后一个元素 用一个数组把该元素右边的区间收集起来 作为右子树进入递归函数

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        TreeNode* node = new TreeNode(0);
        if(nums.size()==1){
            node->val = nums[0];
            return node;
        }
        int maxvalue =0;
        int maxindex =0;
        for(int i=0;i<nums.size();i++){
            if(nums[i]>maxvalue){
                maxvalue=nums[i];
                maxindex=i;
            }
        }
        node->val = maxvalue;
        if(maxindex>0){
            vector<int> vec(nums.begin(),nums.begin()+maxindex);
            node->left = constructMaximumBinaryTree(vec);
        }
        if(maxindex<nums.size()-1){
            vector<int> vec(nums.begin()+maxindex+1,nums.end());
            node->right = constructMaximumBinaryTree(vec);
        }
        return node;
    }
};