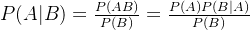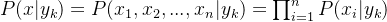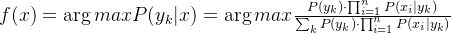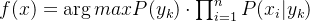目录
一、引言:朴素贝叶斯算法
朴素贝叶斯算法是一种基于贝叶斯定理的监督学习算法,主要用于分类问题,特别是在处理离散特征时。朴素贝叶斯算法是假设特征之间相互独立的,因此称之为“朴素”。尽管这个假设在现实中往往不成立,但它在实际应用中仍然表现出很好的性能,特别是在文本分类(如垃圾邮件检测、情感分析)等领域。
二、朴素贝叶斯概述
朴素贝叶斯是贝叶斯决策理论中的一部分,而贝叶斯决策理论是基于贝叶斯定理的一种统计方法,因此我会先为大家介绍何为“贝叶斯定理”。
2.1 贝叶斯定理
贝叶斯定理是概率论中的一个定理,它描述了在已知的一些条件下,某事件发生的概率。人对某一事件未来会发生的认知,大多取决于该事件或类似事件过去发生的频率。这就是贝叶斯定理的数学模型,它最早由数学家托马斯·贝叶斯提出。
贝叶斯定理的过程可以归纳为:“过去经验”加上“新的证据”得到“修正后的判断”。它提供了一种将新观察到的证据和已有的经验结合起来进行推断的客观方法。
在介绍贝叶斯定理前,先为大家引入先验概率、后验概率和条件概率的概念。
先验概率:是基于统计的概率,是基于以往历史经验和分析得到的结果,不需要依赖当前发生的条件。
条件概率:记事件A发生的概率为P(A),事件B发生的概率为P(B),则在事件B发生的前提下,事件A发生的概率即为条件概率,记为P(A|B)。
后验概率:则是从条件概率而来,由因推果,是基于当下发生了事件之后计算的概率,依赖于当前发生的条件。
贝叶斯公式:假设有随机事件A和B,则贝叶斯公式如下:
-
其中,事件A是要考察的目标事件,P(A)是事件A的初始概率,称为先验概率,它是根据一些先前的观测或者经验得到的概率。
-
B是新出现的一个事件,它会影响事件A。P(B)表示事件B发生的概率。
-
P(B|A)表示在事件A发生的条件下事件B发生的概率,称之为条件概率。
-
P(A|B)表示当事件B发生时事件A发生的概率(也是条件概率),它是我们要计算的后验概率,指在得到一些观测信息后某事件发生的概率。
因此,根据贝叶斯公式可知,先验概率一般是由以往的数据分析或统计得到的概率数据。后验概率是在某些条件下发生的概率,是在得到信息之后再重新加以修正的概率。也就是说,后验概率可以在先验概率的基础上进行修正并得到。
2.2 朴素贝叶斯
朴素贝叶斯是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法。在给定的训练数据集上,朴素贝叶斯学习每个特征与每个类别的概率关系,然后使用贝叶斯定理来预测新实例的类别。
特征条件假设:假设每个特征之间没有联系,给定训练数据集,其中每个样本x都包括n维特征,即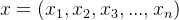
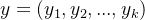
对于给定的新样本x,判断其属于哪个标记的类别,根据贝叶斯定理,可以得到x属于类别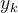
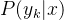
后验概率最大的类别记为预测类别,即: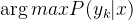
朴素贝叶斯算法对条件概率分布作出了独立性的假设,通俗地讲就是说假设各个维度的特征互相独立,在这个假设的前提上,条件概率可以转化为:
代入上面贝叶斯公式中,得到:
于是,朴素贝叶斯分类器可表示为:
因为对所有的,上式中的分母的值都是一样的,所以可以忽略分母部分,朴素贝叶斯分类器最终表示为:
三、简单的案例实现
接下来是以python中sklearn库自带的乳腺癌数据集为例,分别GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernouliNB(伯努利朴素贝叶斯)3种分类器进行分类预测,并比较输出3种分类器预测的准确率优劣。
3.1 案例过程分析
3.1.1 获取数据集
从python中的sklearn库中导入自带的乳腺癌数据集;
# 从sklearn库中获取自带的乳腺癌数据集
from sklearn import datasets
cancers = datasets.load_breast_cancer()3.1.2 数据处理
用X存放乳腺癌数据集的患者的具体信息,用Y存放该数据集的目标值(乳腺癌数据集的类别);
#数据处理 划分特征向量和目标向量
X = cancers.data
Y = cancers.target
# 打印特征矩阵(属性)
# print(X.shape)
# 打印标签向量矩阵(分类)
# print(Y.shape)
# 描述数据集的详细信息
# print(cancers.DESCR)3.1.3 划分训练集和测试集
在划分训练集和测试集时,调用sklearn库中的train_test_split函数来分割训练集和测试集;
# 划分训练集和测试集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2)3.1.4 创建朴素贝叶斯模型
以下是分别使用GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernouliNB(伯努利朴素贝叶斯)3种方法创建朴素贝叶斯模型的代码;
#利用高斯朴素贝叶斯创建分类器
from sklearn.naive_bayes import GaussianNB
model_linear1 = GaussianNB()
model_linear1.fit(x_train, y_train)
# 使用多项式贝叶斯创建分类器
from sklearn.naive_bayes import MultinomialNB
model_linear2 = MultinomialNB()
model_linear2.fit(x_train, y_train)
# 使用伯努利贝叶斯创建分类器
from sklearn.naive_bayes import BernoulliNB
model_linear3 = BernoulliNB()
model_linear3.fit(x_train, y_train)3.1.5 模型预测与评估
#高斯贝叶斯分类器
train_score1 = model_linear1.score(x_train, y_train)
test_score1 = model_linear1.score(x_test, y_test)
print('高斯贝叶斯训练集的准确率:%f; 测试集的准确率:%f'%(train_score1, test_score1))
preresult = model_linear1.predict(x_test)
print(preresult)
print(y_test)
#多项式贝叶斯分类器
train_score2 = model_linear2.score(x_train, y_train)
test_score2 = model_linear2.score(x_test, y_test)
print('多项式贝叶斯训练集的准确率:%f; 测试集的准确率:%f'%(train_score2, test_score2))
preresult = model_linear2.predict(x_test)
print(preresult)
print(y_test)
#伯努利贝叶斯分类器
train_score3 = model_linear3.score(x_train, y_train)
test_score3 = model_linear3.score(x_test, y_test)
print('伯努利贝叶斯训练集的准确率:%f; 测试集的准确率:%f'%(train_score3, test_score3))
preresult = model_linear3.predict(x_test)
print(preresult)
print(y_test)3.2 代码汇总
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import MultinomialNB
from sklearn.naive_bayes import BernoulliNB
# 从sklearn库中获取自带的乳腺癌数据集
cancers = datasets.load_breast_cancer()
#数据处理 划分特征向量和目标向量
X = cancers.data
Y = cancers.target
# print(X.shape) #打印特征矩阵(属性)
# print(Y.shape) #打印标签向量矩阵(分类)
# print(cancers.DESCR) #描述数据集的详细信息
# x_train为训练集的特征值,y_train为训练集的目标值,x_test为测试集的特征值,y_test为测试集的目标值
# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2)
#三种朴素贝叶斯分类方式
#高斯贝叶斯分类器
model_linear1 = GaussianNB()
model_linear1.fit(x_train, y_train)
train_score1 = model_linear1.score(x_train, y_train)
test_score1 = model_linear1.score(x_test, y_test)
print('高斯贝叶斯训练集的准确率:%f; 测试集的准确率:%f'%(train_score1, test_score1))
preresult = model_linear1.predict(x_test)
print(preresult)
print(y_test)
#多项式贝叶斯分类器
model_linear2 = MultinomialNB()
model_linear2.fit(x_train, y_train)
train_score2 = model_linear2.score(x_train, y_train)
test_score2 = model_linear2.score(x_test, y_test)
print('多项式贝叶斯训练集的准确率:%f; 测试集的准确率:%f'%(train_score2, test_score2))
preresult = model_linear2.predict(x_test)
print(preresult)
print(y_test)
#伯努利贝叶斯分类器
model_linear3 = BernoulliNB()
model_linear3.fit(x_train, y_train)
train_score3 = model_linear3.score(x_train, y_train)
test_score3 = model_linear3.score(x_test, y_test)
print('伯努利贝叶斯训练集的准确率:%f; 测试集的准确率:%f'%(train_score3, test_score3))
preresult = model_linear3.predict(x_test)
print(preresult)
print(y_test)
3.3 运行结果说明
以下是GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernouliNB(伯努利朴素贝叶斯)3种分类器进行分类预测的结果运行图;
(1)高斯朴素贝叶斯分类器
(2)多项式朴素贝叶斯分类器
(3)伯努利朴素贝叶斯分类器
四、实验总结
通过构建朴素贝叶斯分类器模型并对乳腺癌数据集进行分类,我体会到朴素贝叶斯算法的简洁性和解释性。朴素贝叶斯分类器的结构非常直观,易于理解,这使得它在很多领域都有广泛的应用。同时,也需要注意朴素贝叶斯算法对特征独立性的假设,这可能会降低模型的准确性。