💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学,什么是电的时候,不要觉得这些问题搞笑。哲学是科学之母,哲学就是追究终极问题,寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能让人胸中升起一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它居然给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
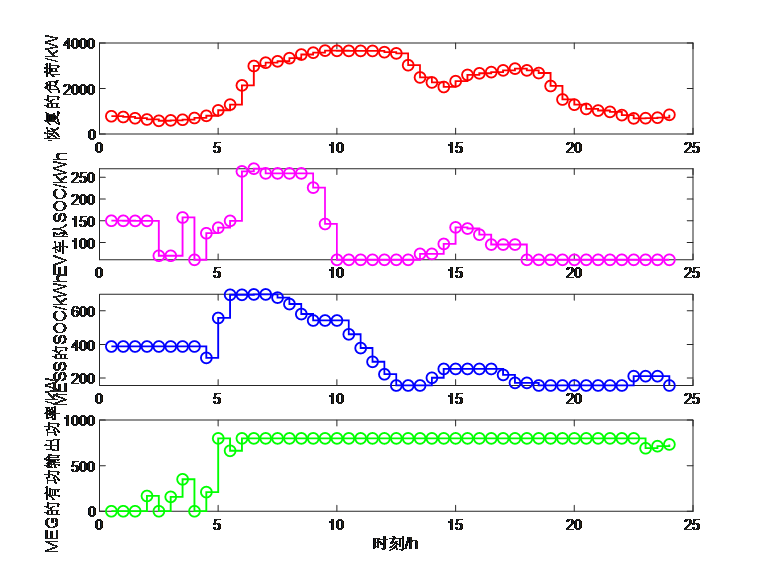
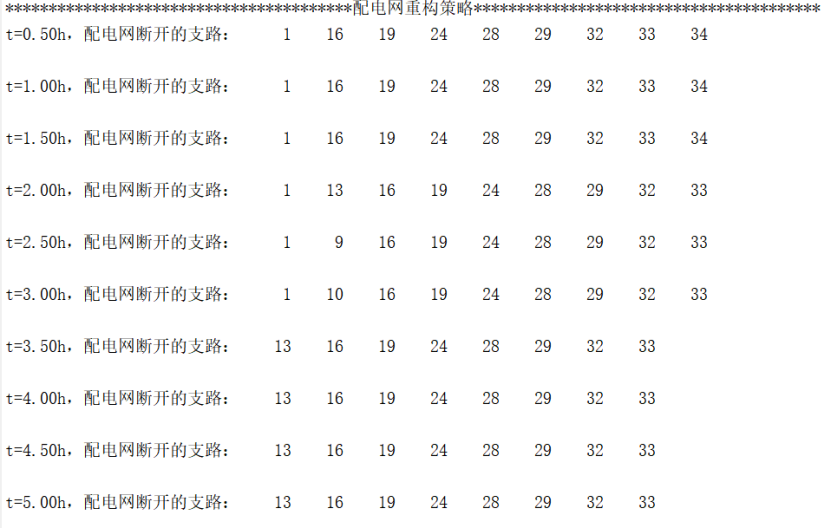
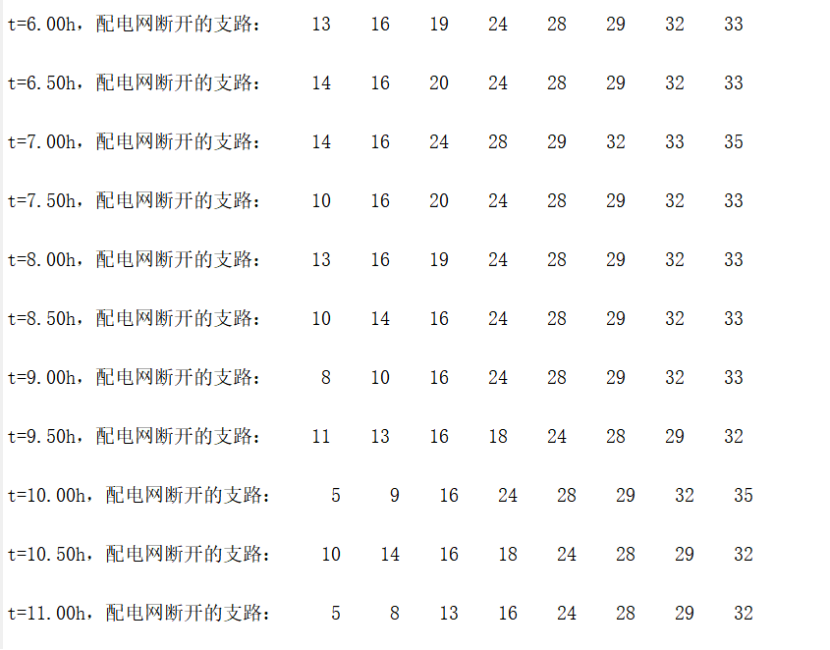
本文是上述SCI一区论文的部分复现,即采用求解MPS动态调度策略的部分。
Abstract:
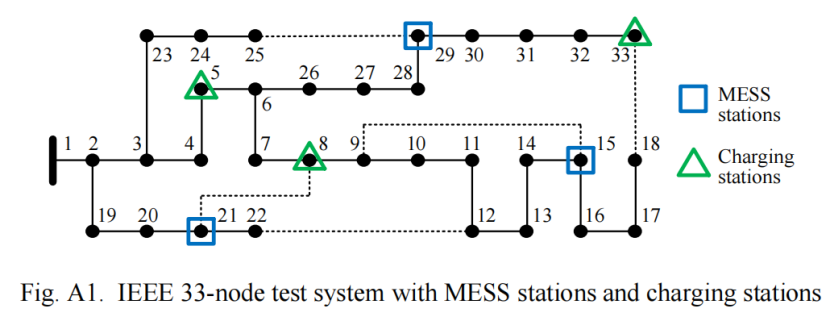
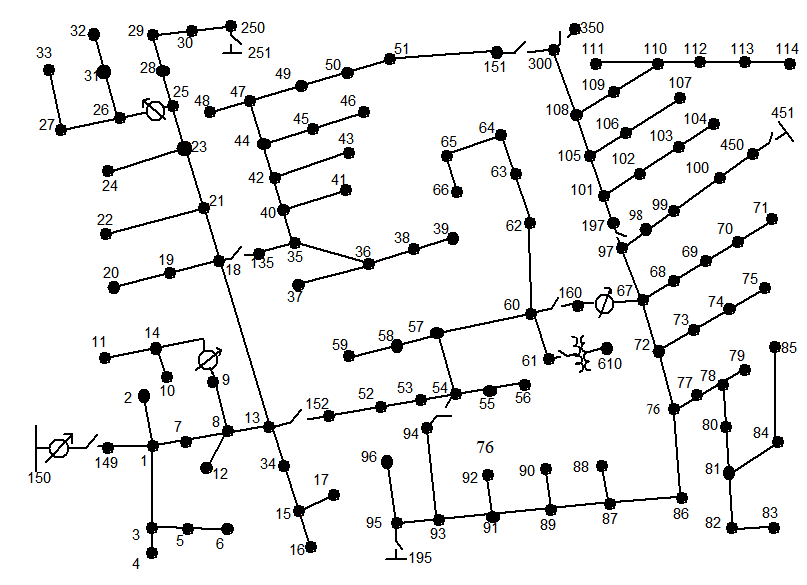
Mobile power sources (MPSs), including electric vehicle fleets, truck-mounted mobile energy storage systems, and mobile emergency generators, have great potential to enhance distribution system (DS) resilience against extreme weather events. However, their dispatch is not well investigated. This paper implements resilient routing and scheduling of MPSs via a two-stage framework. In the first stage, i.e., before the event, MPSs are pre-positioned in the DS to enable rapid pre-restoration, in order to enhance survivability of the electricity supply to critical loads. DS network is also proactively reconfigured into a less impacted or stressed state. A two-stage robust optimization model is constructed and solved by the column-and-constraint generation algorithm to derive first-stage decisions. In the second stage, i.e., after the event, MPSs are dynamically dispatched in the DS to coordinate with conventional restoration efforts, so as to enhance system recovery. A novel mixed-integer programming model that resolves different timescales of MPS dispatch and DS operation, coupling of road and power networks, etc., is formulated to optimize dynamic dispatch of MPSs. Case studies conducted on IEEE 33-node and 123-node test systems demonstrate the proposed method's effectiveness in routing and scheduling MPSs for DS resilience enhancement.
摘要:
移动电源(MPSs),包括电动汽车车队、车载移动储能系统和移动应急发电机,在增强配电系统(DS)对极端天气事件的抵御能力方面具有巨大潜力。然而,他们的派遣情况并没有得到很好的调查。本文通过两阶段框架实现了MPS的弹性路由和调度。在第一阶段,即在事件发生之前,MPS被预先放置在DS中,以实现快速预恢复,从而提高关键负载的电力供应的生存能力。DS网络也主动重新配置为受影响较小或压力较小的状态。构建了一个两阶段鲁棒优化模型,并使用列约束生成算法求解,以得出第一阶段的决策。在第二阶段,即在事件发生后,在DS中动态调度MPS以协调常规恢复工作,从而增强系统恢复能力。一种新型的混合整数规划模型,解决了MPS调度和DS运行的不同时间尺度、道路和电力网络的耦合等问题,以优化MPS的动态调度。在IEEE 33节点和123节点测试系统上进行的案例研究表明,所提出的方法在路由和调度MPS以提高DS弹性方面是有效的。

📚2 运行结果

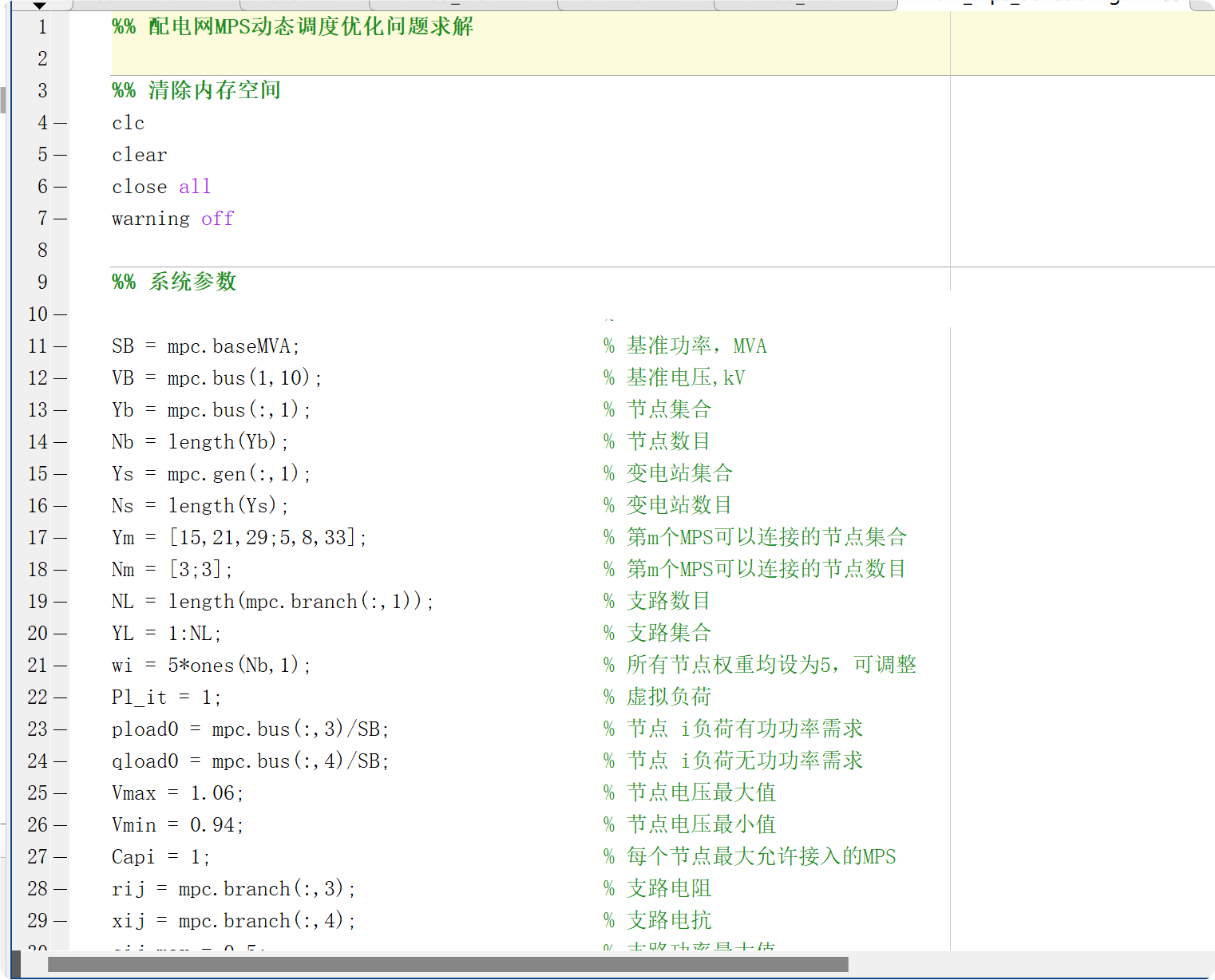
部分代码:
%% 配电网MPS动态调度优化问题求解
%% 清除内存空间
clc
clear
close all
warning off
%% 系统参数
Copyright; % 配电网参数,脆弱支路和非脆弱支路,负荷曲线
SB = mpc.baseMVA; % 基准功率,MVA
VB = mpc.bus(1,10); % 基准电压,kV
Yb = mpc.bus(:,1); % 节点集合
Nb = length(Yb); % 节点数目
Ys = mpc.gen(:,1); % 变电站集合
Ns = length(Ys); % 变电站数目
Ym = [15,21,29;5,8,33]; % 第m个MPS可以连接的节点集合
Nm = [3;3]; % 第m个MPS可以连接的节点数目
NL = length(mpc.branch(:,1)); % 支路数目
YL = 1:NL; % 支路集合
wi = 5*ones(Nb,1); % 所有节点权重均设为5,可调整
Pl_it = 1; % 虚拟负荷
pload0 = mpc.bus(:,3)/SB; % 节点 i负荷有功功率需求
qload0 = mpc.bus(:,4)/SB; % 节点 i负荷无功功率需求
Vmax = 1.06; % 节点电压最大值
Vmin = 0.94; % 节点电压最小值
Capi = 1; % 每个节点最大允许接入的MPS
rij = mpc.branch(:,3); % 支路电阻
xij = mpc.branch(:,4); % 支路电抗
sij_max = 0.5; % 支路功率最大值
Pm_max = [300,500,800]/(SB*1e3); % 第m个MPS的输出有功功率上限
Qm_max = [500,776,600]/(SB*1e3); % 第m个MPS的输出无功功率上限
G1 = 5; % 脆弱支路的最大故障数
G2 = 3; % 非脆弱支路的最大故障数
K1 = Nb - Ns; % 足够大的正数K1
K2 = Nb; % 足够大的正数K2
YT = 0.5:0.5:24; % 控制时段集合
NT = 48; % 控制时段数
dt = 0.5; % 一个控制时段的持续时间
tr_ij = ... % MPS从节点i到节点j的通行时间。
{[0,4,2;4,0,2;2,2,0],[0,2,2;2,0,4;2,4,0]};
SOC0 = 0.5*[300;776]/(SB*1e3); % 初始荷电状态
nc = 0.95; % 充电效率
nd = 0.95; % 放电效率
SOC_max = 0.9*[300;776]/(SB*1e3); % 荷电状态上限
SOC_min = 0.2*[300;776]/(SB*1e3); % 荷电状态下限
tp = 0.25/(SB*1e3); % EV车队能耗率
YL_RCS = 1:37; % 拥有自动开关的支路集合
dm = 0.002; % MPS的运输成本系数
Zm = 0.000015; % MPS电池老化速度
CBm = 0.01; % MPS单位充放电价格
Lij0 = ones(NL,1); % 初始支路开断状态
Lij0([2,10,13,15,24]) = 0;
branch_to_node = zeros(Nb,NL); % 节点的上游支路
branch_from_node = zeros(Nb,NL); % 节点的下游支路
for k = 1:NL
branch_to_node(mpc.branch(k,2), k) = 1;
branch_from_node(mpc.branch(k,1), k) = 1;
end
Ysrc = cell(1,NT); % t时刻的虚拟电源节点集合
L_off = cell(1,NT); % t时刻仍未修复的支路
It = zeros(1,NT); % 在t时刻形成的孤岛数
for t = 1:NT
if t >= 1 && t <= 6
L_off{t} = [1,19,33,16,32,29,28,24];
Ysrc{t} = [1,2,25,30,33];
It(t) = 5;
elseif t >= 7 && t <= 12
L_off{t} = [19,33,16,32,29,28,24];
Ysrc{t} = [1,25,30,33];
It(t) = 4;
elseif t >= 13 && t <= 18
L_off{t} = [33,16,32,29,28,24];
Ysrc{t} = [1,25,30,33];
It(t) = 4;
elseif t >= 19 && t <= 26
L_off{t} = [16,32,29,28,24];
Ysrc{t} = [1,25,30,33];
It(t) = 4;
elseif t >= 27 && t <= 32
L_off{t} = [32,29,28,24];
Ysrc{t} = [1,25,30];
It(t) = 3;
elseif t >= 33 && t <= 40
L_off{t} = [29,28,24];
Ysrc{t} = [1,25];
It(t) = 2;
elseif t >= 41 && t <= 44
L_off{t} = [28,24];
Ysrc{t} = 1;
It(t) = 1;
elseif t >= 45 && t <= 48
L_off{t} = [24];
Ysrc{t} = 1;
It(t) = 1;
end
end
%% 设决策变量
bimt_EV = binvar(Nm(2),NT); % 0-1变量,如果EV预配置到节点i,取值为1,否则取值为0。
bimt_MESS = binvar(Nm(1),NT); % 0-1变量,如果MESS预配置到节点i,取值为1,否则取值为0。
bimt_MEG = binvar(Nm(1),NT); % 0-1变量,如果MEG预配置到节点i,取值为1,否则取值为0。
ymt_EV = binvar(1,NT); % 0-1变量,如果EV在t时刻正在行驶,则取值为1,否则取值为0。
ymt_MESS = binvar(1,NT); % 0-1变量,如果MESS在t时刻正在行驶,则取值为1,否则取值为0。
ymt_MEG = binvar(1,NT); % 0-1变量,如果MEG在t时刻正在行驶,则取值为1,否则取值为0。
cmt_EV = binvar(1,NT); % 0-1变量,如果EV在t时刻正在充电,则取值为1,否则取值为0。
cmt_MESS = binvar(1,NT); % 0-1变量,如果MESS在t时刻正在充电,则取值为1,否则取值为0。
dmt_EV = binvar(1,NT); % 0-1变量,如果EV在t时刻正在放电,则取值为1,否则取值为0。
dmt_MESS = binvar(1,NT); % 0-1变量,如果MESS在t时刻正在放电,则取值为1,否则取值为0。
cpmt_EV = sdpvar(1,NT); % EV在t时刻充电功率。
cpmt_MESS = sdpvar(1,NT); % MESS在t时刻充电功率。
dpmt_EV = sdpvar(1,NT); % EV在t时刻放电功率。
dpmt_MESS = sdpvar(1,NT); % MESS在t时刻放电功率。
SOC_mt_EV = sdpvar(1,NT); % EV在t时刻的荷电状态
SOC_mt_MESS = sdpvar(1,NT); % MESS在t时刻的荷电状态
gp_mt = sdpvar(3,NT); % MPS在t时刻的有功输出
gq_mt = sdpvar(3,NT); % MPS在t时刻的无功输出
Lijt = binvar(NL,NT); % 0-1变量,取值为1时表示支路闭合,取值为0时表示支路断开
git = cell(1,NT); % 虚拟电源的出力
for t = 1:NT
git{t} = sdpvar(It(t),1);
end
fijt = sdpvar(NL,NT); % 支路ij的虚拟功率
pload = sdpvar(Nb,NT); % 节点i的实际有功负荷
qload = sdpvar(Nb,NT); % 节点i的实际无功负荷
Pi = sdpvar(Nb,NT); % 节点i注入有功功率
Qi = sdpvar(Nb,NT); % 节点i注入无功功率
pf_ijt = sdpvar(NL,NT); % 支路ij的有功功率
qf_ijt = sdpvar(NL,NT); % 支路ij的无功功率
vit = sdpvar(Nb,NT); % 节点i的电压平方
%% 约束条件
省略。。。。。。。
%% 目标函数
objective = sum(wi.*sum(pload, 2)) - dm*sum(ymt_EV + ymt_MESS + ymt_MEG) - Zm*CBm*sum(cpmt_EV + dpmt_EV + cpmt_MESS + dpmt_MESS);
%% 设求解器
% gurobi求解器
ops = sdpsettings('verbose', 3, 'solver', 'gurobi','showprogress',1, 'debug', 1);
ops.gurobi.TimeLimit = 600; % 运行时间限制为10min
ops.gurobi.MIPGap = 0.01; % 收敛精度限制为0.01
sol = optimize(Constraints, -objective, ops);
%% 分析错误标志
if sol.problem == 0
disp('求解成功');
else
disp('运行出错');
yalmiperror(sol.problem)
end
%% 展示运行结果
show_result;
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1] Lei S , Chen C , Zhou H ,et al.Routing and Scheduling of Mobile Power Sources for Distribution System Resilience Enhancement[J].IEEE Transactions on Smart Grid, 2019:5650-5662.DOI:10.1109/TSG.2018.2889347.
🌈4 Matlab代码实现
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取