注:本篇文章针对PID算法的类型做了较为全面的整理和归纳,有的类型理解较为困难,但是希望读者能有所了解和印象,不懂的地方可以通过查阅相关书籍和网站自行领悟。
文章末尾附有PID相关资料书籍和知识总结的链接,需要的请私信我,我会第一时间回复。本人知识有限,很多内容都是通过总结前人的智慧,站在巨人的肩膀上来和大家共享知识,一同进步。
最后,希望我们能一起奔跑,逐梦不止!
本篇文章是对PID算法的原理和类型做了较为全面的概述。具体的算法实现和运用请读者转看:
PID算法详解(代码详解篇),位置式PID、增量式PID(通用)_小小_扫地僧的博客-CSDN博客
一.什么是PID算法
在了解PID算法之前,我个人觉得有必要先介绍一下PID的全称,为什么呢,因为顾名方可思义。了解其名子的含义,更加有助于我们理解该算法的原理,也能帮助我们灵活地运用PID算法。
先来举个例子说明PID的运用:
比如你骑自行车,如何控制才能确保自行车不倒呢?
会骑车的都知道,当车的重心向一个方向倾斜时,笼头要向同方向打。而且这个打的角度,与重心倾斜的角度是成正比的,倾斜度越大,笼头角度也要打得越多。——这就是P(比例)控制。
打完笼头后,车是不会倒了,但是并不意味着你的车轮就能走直线,可能还会歪歪扭扭。为什么呢?因为还存在静态误差,需要在骑的过程中,不断地“微调”修正,才能确保行车路径笔直。——这就是l(积分)控制。
有时为了急转弯,我们会把笼头打过头,接下来就要赶紧回打,以抵消刚才的过调,求得平衡。——这就是D(微分)控制。
骑车时,人的大脑就是控制器,眼睛是传感器,手足是执行器。
1.简介
PID即:Proportional(比例)、Integral(积分)、Differential(微分)的缩写。顾名思义,PID控制算法是结合比例、积分和微分三种环节于一体的控制算法,它是连续系统中技术最为成熟、应用最为广泛的一种控制算法。
2.用途
适用于对被控对象模型了解不清楚的场合。实际运行的经验和理论的分析都表明,运用这种控制规律对许多工业过程进行控制时,都能得到比较满意的效果。PID控制的实质就是根据输入的偏差值,按照比例、积分、微分的函数关系进行运算,运算结果用以控制输出。
接下来我会分别介绍PID的各个组成部分Proportional(比例)、Integral(积分)、Differential(微分)
最后将Proportional(比例)、Integral(积分)、Differential(微分)这三部分组合到一起,就是PID算法
-
PID控制原理图解


3.位置式PID控制算法
按模拟PID控制算法,以一系列的采样时刻点kT代表连续时间t,以矩形法数值积分近似代替积分,以一阶后向差分近似代替微分,即:

4.增量式PID控制算法
当执行机构需要的是控制量的增量(例如驱动步进电机〉时,应采用增堂式PID控制。
根据递推原理可得:
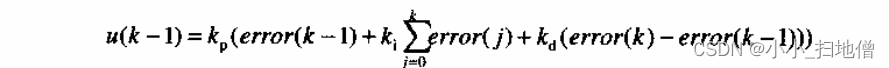

-
积分分离PID控制算法
在普通PID 控制中引入积分环节的目的,主要是为了消除静差,提高控制精度。但在过程的启动、结束或大幅度增减设定时,短时间内系统输出有很大的偏差,会造成PID运算的积分积累,致使控制量超过执行机构可能允许的最大动作范围对应的极限控制量,引起系统较大的超调,甚至引起系统较大的振荡,这在生产中是绝对不允许的。
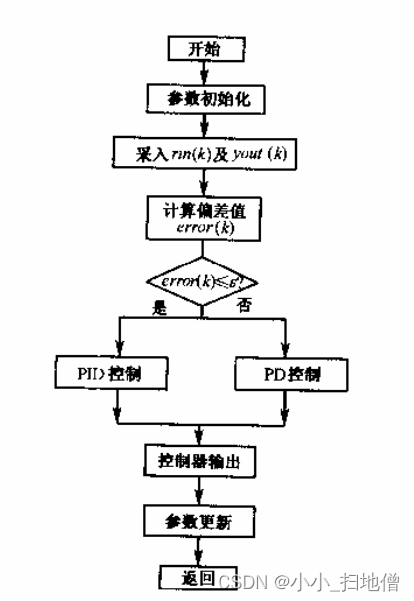
积分分离控制基本思路是:当被控量与设定值偏差较大时,取消积分作用,以免由于积分作用使系统稳定性降低,超调量增大;当被控量接近给定值时,引入积分控制,以便消除静差,提高控制精度。其具体实现步骤如下:


根据积分分离式PID控制算法得到其程序框图如图所示:
5.抗积分饱和PID控制算法
1.积分饱和现象
所谓积分饱和现象是指若系统存在: ‘个方向的偏差,PID控制器的输出由于积分作用的不断累加而加人、从而导致执行机构达到极限位置mae (例如阀门开度达到最大),如图1-20所示,若控制器输出u(k)继续增大,阀门开度不可能再增大,此时就称讣算机输出控制量超比了止常运行范围而进入了饱和区.。﹒旦系统出现反向偏差,u(k)逐渐从饱和区退出。进入饱和x.愈深则退出饱和区所需时间愈长。在这段时间内,执行机构仍停留在极限位置而不能随偏差反向立即做出相应的改变,这时系统就像失去控制一样,造成拧制性能恶化。这种现象称为积分饱和现象或积分失控现象。

2.抗积分饱和算法
作为防止积分饱和的方法之一就足抗积分饱和法,该方法的思路是在计算u(k)时,首先判断卜-一时刻的控制量u(k一1)是否已超出限制范围:

6.变速积分PID算法
在普通的PID 控制算法巾,出于积分系数k是常数,所以在整个控制过程中,积分增量不变。而系统对积分项的要求是.系统偏差大时积分作用应减弱甚至全无,而在偏差小时则应加强。积分系数取大了会产生超调,共至积分饱和,取小了又迟迟不能消除静差。因此,如何根据系统偏差大小改变积分的速度,对于提高系统品质是很重要的。变速积分PID可较好地解决这一问题
变速积分PID的基本思想是设法改变积分项的累加速度,使其与偏差大小相对应:偏越人,积分越慢,反之则越快。

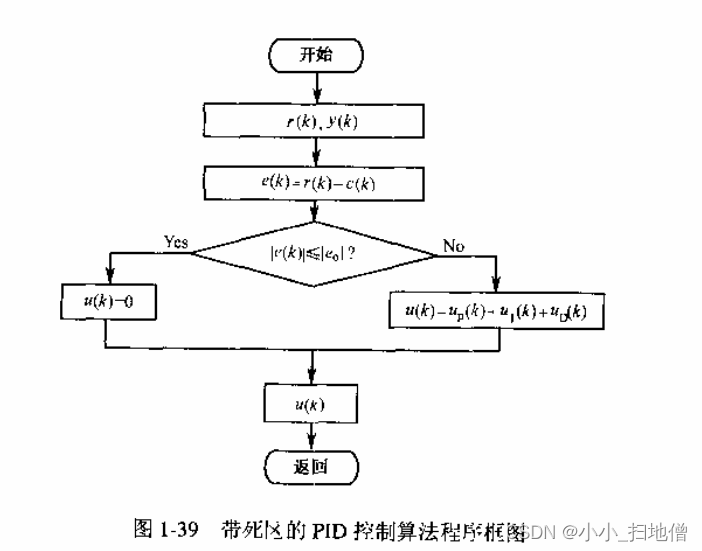
7.带死区的PID算法

8.基于前馈补偿的PID控制算法
在高精度伺服控制中,前馈控制可用来提高系统的跟踪性能。经典控制理论中的前馈控制设计是基于复合控制思想,当闭环系统为连续系统时,使前馈环节与闭环系统的传递函数之积为1,从而实现输出完全复现输入。作者利用前馈控制的思想,针对PID控制设计了前馈补偿,以提高系统的跟踪性能,其结构如图1-42所示。
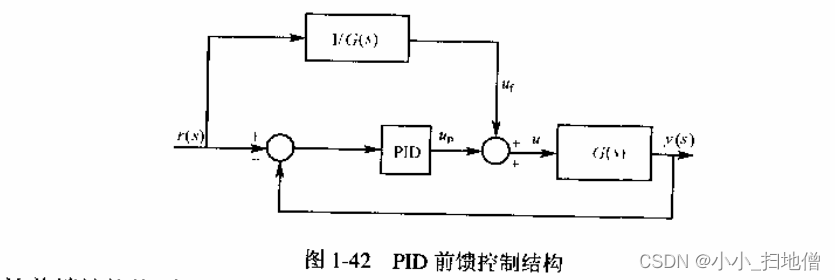
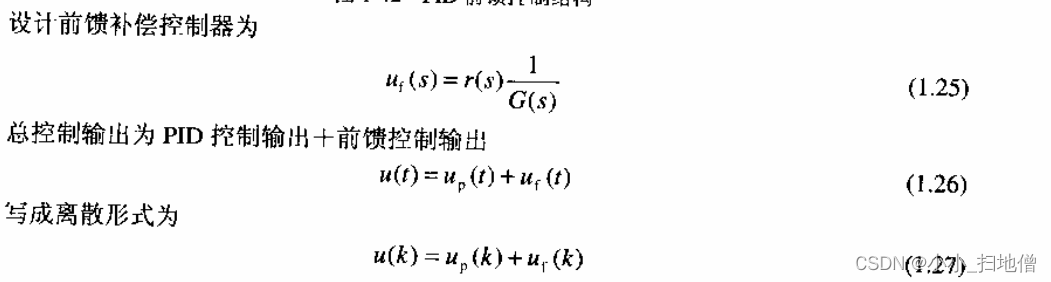
9.梯形积分PID控制算法
在PD 控制律中积分项的作用是消除余差,为了减小余差,应提高积分项的运算精度,为此,可将矩形积分改为梯形积分。梯形积分的计算公式为
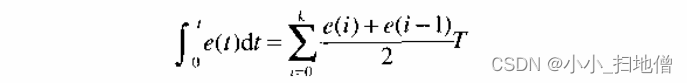
10.变速积分PID 算法
在普通的PID挖制算法中,由于积分系数k是常数,所以在:整个控制过程中,积分增量不变。而系统对积分项的要求是.系统偏差大时积分作用应减弱甚至全无,而在偏差小时则应加强。积分系数取大了会产生超调,共至积分饱和,取小了又迟迟不能消除静差。因此,如何根据系统偏差大小改变积分的速度,对于提高系统品质是很重要的。变速积分PID可较好地解决这―问题-
变速积分PID的基本思想是设法改变积分项的累加速度,使其与偏差大小相对应:偏箦越人,积分越慢,反之则越快。
为此,设置系数 f(e(k)),它是e(k)的函数。当|e(k)|增大时,f减小,反之增人。变速积分的PID积分项表达式为
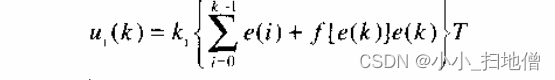
系数f与偏差当前值|e(k)的关系可以是线性的或非线性的,可设为
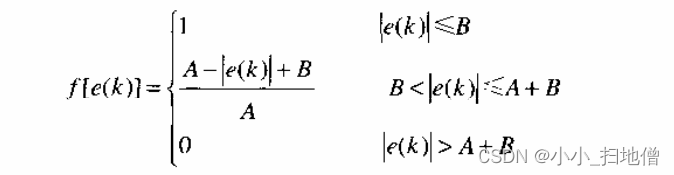

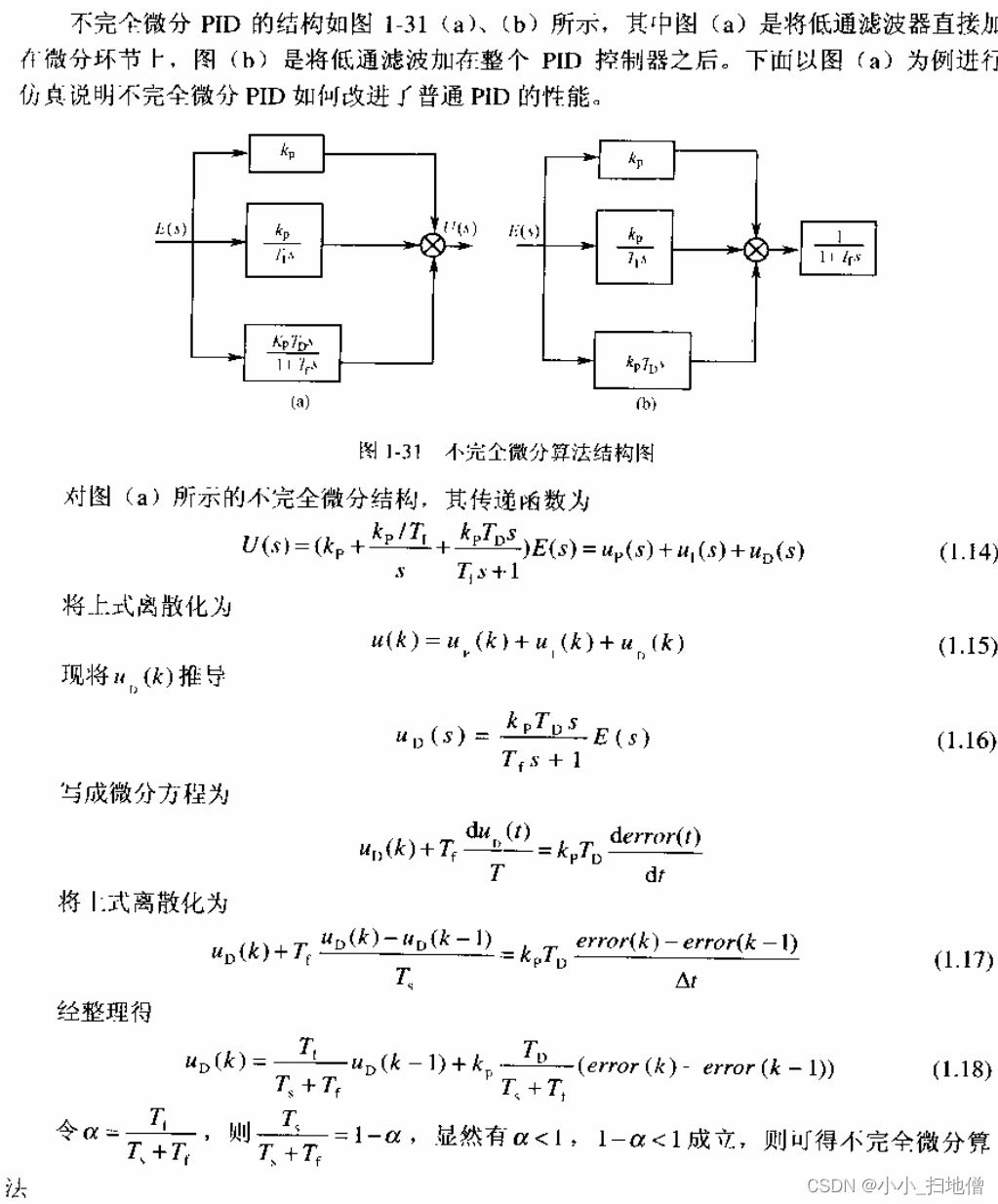
11.不完全微分PID控制算法
在: PID 控制中,微分信号的引入可改善系统的动态特性,但也易引进高频F扰,在误差拢动突变时尤其显}出微分项的不足。若在控制算.法中加入低通滤波器,则可使系统性能得到改善。
克服上述缺点的方法之一是在 PID 算法中加入一个一阶惯性环节(低通滤波器)

可使系统性能得到改善.

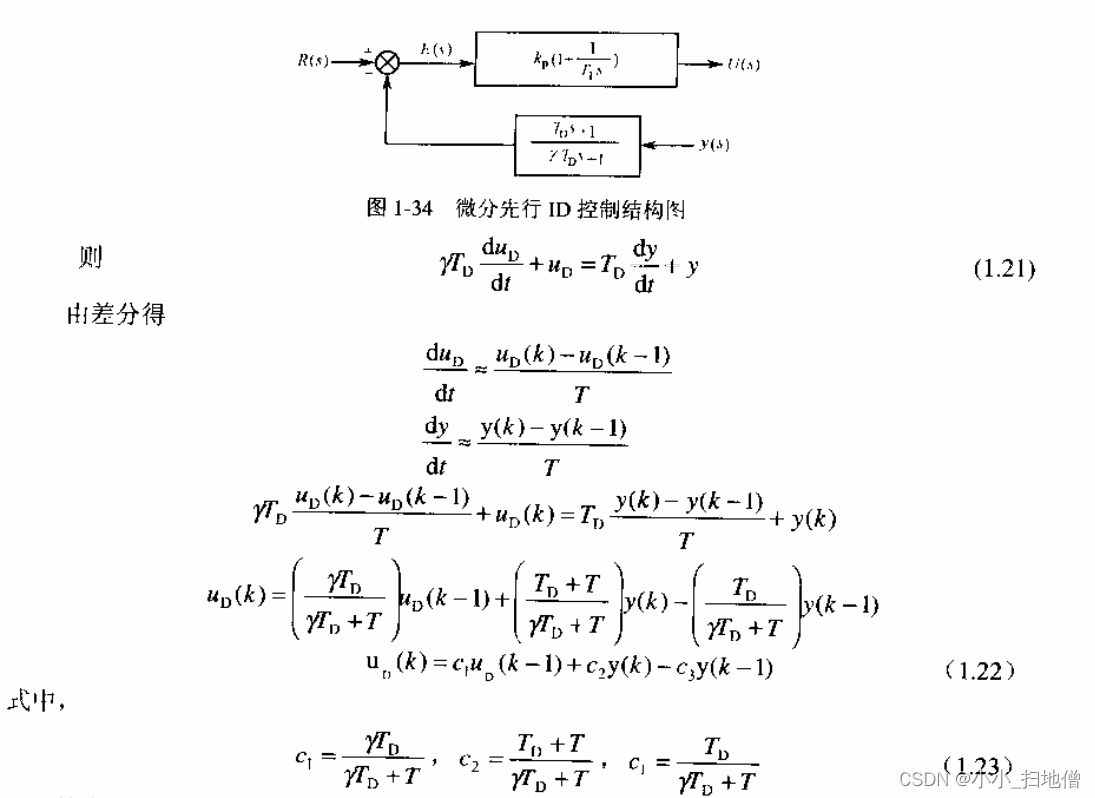
12.微分先行PD控制算法
微分先行PID 控制的结构如图1-34所示,其特点是只对输出量yout(k)进行微分,而对给定值rin(k)不作微分。这样,在改变给定值时,输出不会改变,而被控量的变化通常是比较缓和的。这种输出量先行微分控制适用于给定值rin(k)频繁升降的场合,可以避免给定值升降时所引起的系统振荡,从而明显地改善了系统的动态特性。
令微分部分的传递函数为

13.步进式PID控制算法
在较大阶跃响应时,很容易产生超调。采用步进式积分分离PID控制,该方法不直接对阶跃信号进行响应,而是使输入指令信号一步一步地逼近所要求的阶跃信号,可使对象运行平稳,适用于高精度伺服系统的位置跟踪。
这是相关PID资料,需要的读者请私信我或者入群领取(815239036),收到后我会第一时间回复: