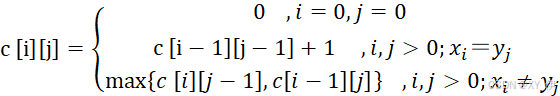目录
一、实验目的
掌握动态规划求解问题的思想;针对不同的问题,会利用动态规划进行设计求解以及时间复杂度分析,并利用JAVA/C/C++等编程语言开展编码实践(语言自选)。
理解两组序列的最长公共子序列问题,能够利用动态规划,开展问题的最优子结构性质分析、子结构递归关系构建、自底向上最优值求解以及最优解构造。
二、实验环境
1、机房电脑 Window11
2、Eclipse/Dev-C++等
三、实验内容
实验要求:
①掌握动态规划求解问题的策略及思路;
①基于动态规划开展最长公共子序列问题的算法设计与优化;
③对上述算法进行时间复杂性分析,并输出程序运行时间及运行结果。
实验原理:
1、按照自己的理解,总结描述动态规划求解问题的思路策略;
动态规划是针对于递归分治所存在的缺点而设计出来的算法思想,递归分治算法存在大量子问题被重复计算,效率低下的问题,如下图,多个子节点在不同的递归表达式中被重复计算,增加了算法冗余度。
而在动态规划的算法中,虽然与分治法类似,但是动态规划却在思考如果能够保存已解决的子问题的答案,而在需要时再直接找出已求得的节点,就可以避免大量重复计算,从而得到多项式时间算法,这样就可以避免同一个问题被多次计算的问题,如下图。
动态规划是解决具有重叠子问题和最优子结构性质的问题的有效方法。 它的基本原理是将大问题分解为小问题,通过保存中间结果来避免重复计算,从而提高算法的效率。动态规划方法所耗时往往远少于一般解法。
2、针对最长公共子序列问题,如何利用动态规划进行建模设计与优化;
①给出求解过程及建模思路,以及子序列的构造原理;
用动态规划算法可以解决最长公共子序列这一经典问题,公共子序列问题,寻找两个字符串中都存在的最长子序列,这个最长子序列可以不是连续的,但是要保证其相对顺序一样
先找出最优问题特点:设有两个序列X={
x1 , x2
,…, xm
}和Y={
y1
, y2
,…, yn
}的最长公共子序列为Z={
z1
, z2
,…, zk
}
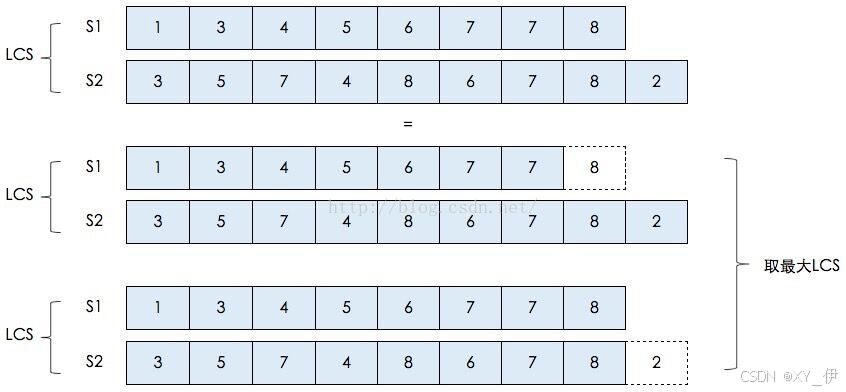
(1)若xm =yn
,则zk
=xm
=yn
,且zk-1
是xm-1
和yn-1
的最长公共子序列。
(2)若xm ≠yn
且Zk
≠xm
,则zk
是xm-1
和Y的最长公共子序列。
(3)若xm ≠yn
且Zk
≠yn
,则zk
是X和yn-1
的最长公共子序列。
所以2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列,最长公共子序列问题具有最优子结构性质。
定义递归关系;根据以上已经求得的最长公共子序列问题的性质,我们可以知道如下图:
根据此递归关系我们可以求得以下递归方程,其中c [i][j]数组记录序列的最长公共子序列长度。首先当i=0或j=0时,有一个序列为空,所以c [i][j]=0
该算法的时间复杂度为O(m n)
②针对序列X={a,b,a,d,e},Y={a,r,f,a,e},给出子结构二维数组。
根据上列的c[i][j]表达式可以求出:
| X Y | ∅ | a | b | a | d | e |
| ∅ | 0 | 0 | 0 | 0 | 0 | 0 |
| a | 0 | 1 | 1 | 1 | 1 | 1 |
| r | 0 | 1 | 1 | 1 | 1 | 1 |
| f | 0 | 1 | 1 | 1 | 1 | 1 |
| a | 0 | 1 | 1 | 2 | 2 | 2 |
| e | 0 | 1 | 1 | 2 | 2 | 3 |
由此表可知公共子序列长度为3,是aae
四、核心代码
int c[10001][10001]; //数组记录序列的最长公共子序列长度
int b[10001][10001]; //标记是递归关系中的哪一种情况
void LCS_num(int m,int n,char *X,char *Y){
for(int i=1;i<=m;i++){ //首先当i=0或j=0时,代表有一个序列为空,所以c [i][j]=0
c[i][0]=0;
}
for(int j=1;j<=n;j++){
c[0][j]=0;
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(X[i-1]==Y[j-1]){ //当X序列的第i个元素和Y序列的第j个元素相等时
c[i][j]=c[i-1][j-1]+1; //那么当前i元素一定再最长公共子序列里,长度+1
b[i][j]=1; //b数组用来标记1,表示此情况
}else if(c[i-1][j]>=c[i][j-1]){ //如果不相等,此时分两种情况进行比较
c[i][j]=c[i-1][j];
b[i][j]=2;
}else{
c[i][j]=c[i][j-1];
b[i][j]=3;
}
}
}五、记录与处理
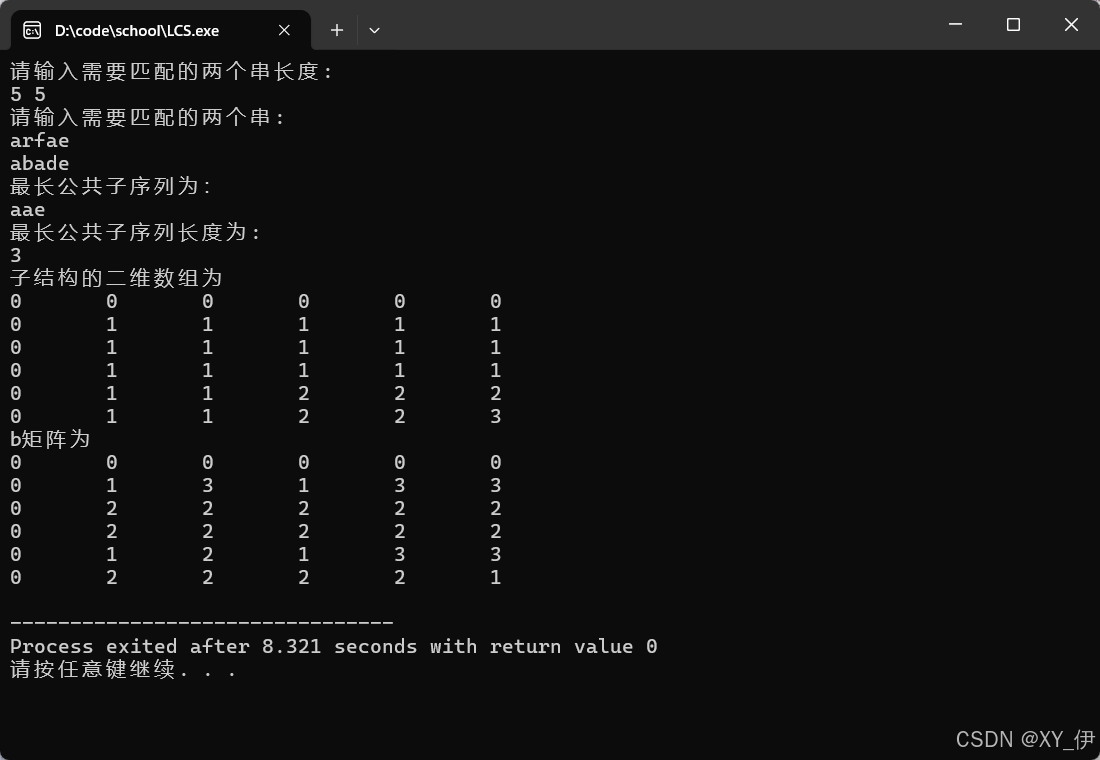
实验数据及结果分析:
输入实例中的数据,与自行计算的结果一致,同时还输出了b数组,代表每个字符进行匹配的情况。
b数组标记1,表示X序列的第i个元素和Y序列的第j个元素相等;
b数组标记2,表示{X减去最后一个元素}与Y的最长公共子序列的序列较大;
b数组标记3,X与 {Y减去最后一个元素}的最长公共子序列的序列较大。
最长公共子序列为3,aae
六、思考与总结
动态规划算法通常分为以下几个步骤:
找出最优问题特点:明确问题的最优解具有什么样的性质,这是使用动态规划的前提。
定义递归关系:根据问题的最优子结构,建立子问题之间的递归关系,这是动态规划的核心。
自底向上计算每一步结果:利用递归关系,从最小的子问题开始,逐步求解更大的子问题,直到求解出原问题。
构造最优解:根据保存的中间结果,构造出原问题的最优解。
七、完整报告和成果文件提取链接
完整可运行代码以及相关实验报告以下链接可获取:
链接: https://pan.baidu.com/s/1iss6-C2nxZQGkEpo-WDn0A?pwd=g5cg 提取码: g5cg