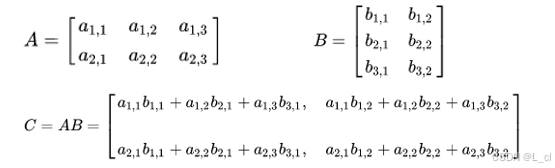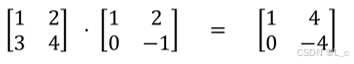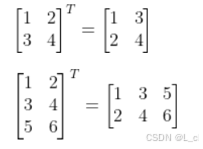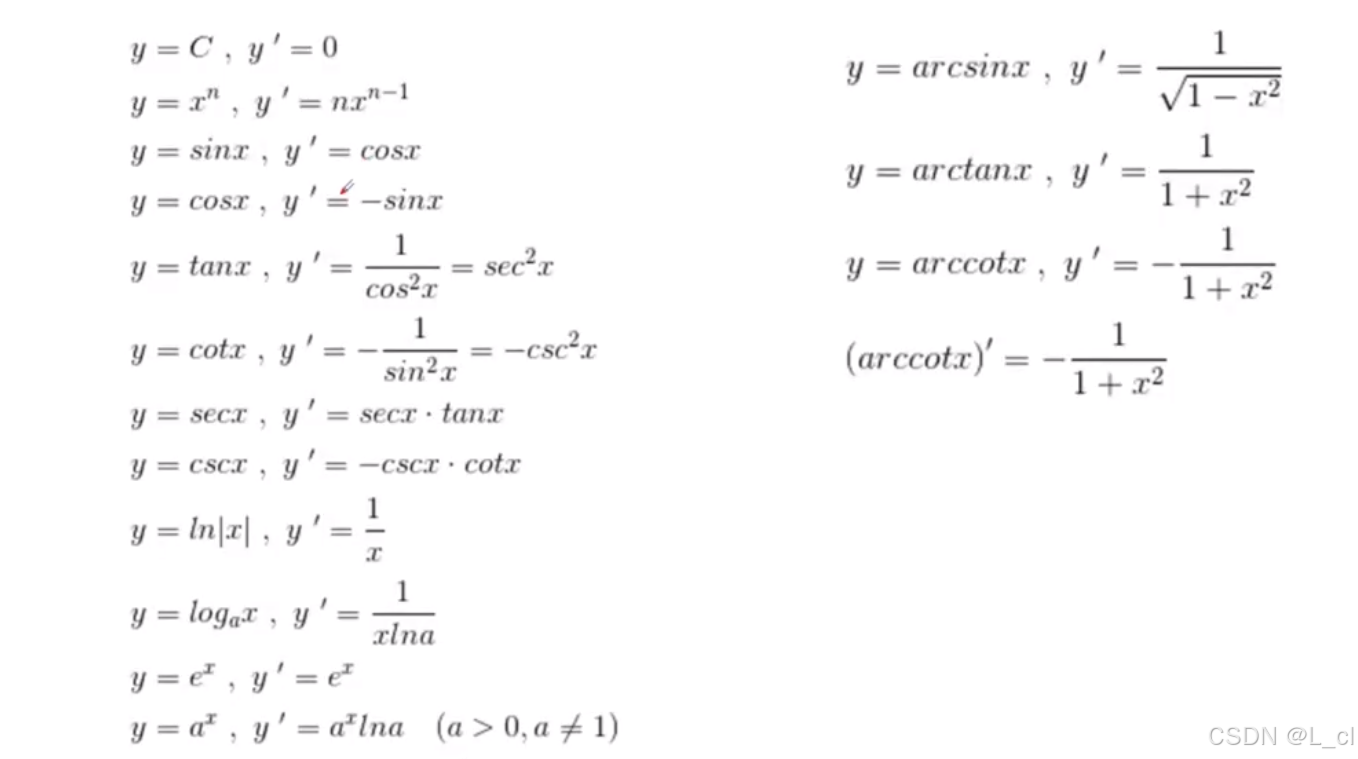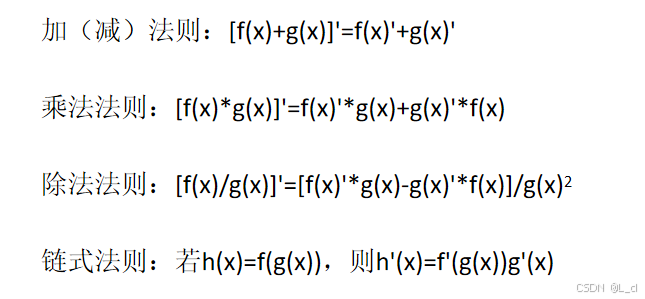此去经年,应是良辰美景虚设
—— 24.11.28
一、线性代数
1.标量和向量
① 标量 Scalar
一个标量就是一个单独的数
② 向量 Vector
一个向量是一列数
可以把向量看作空间中的点,每个元素是不同坐标轴上的坐标
向量中有几个数,就叫作几维向量;如四维向量:[1,2,3,4]
2.向量运算
① 向量加和
对位相加
A + B = B + A 需要维度相同
eg:[1, 2] + [3, 4] = [4, 6]
② 向量内积
对位相乘再相加
A * B = B * A 需要维度相同
eg:[1, 2] * [3, 4] = 3 + 8 = 11
③ 向量夹角余弦值
两个向量做内积 / 两个向量的模长乘积
夹角θ越小,说明两向量越接近
Cosθ = A * B / |A| * |B| 需要维度相同
向量的模 |A| = (x1^2+x2^+…+xn^2)^1/2
需要维度相同
3.矩阵 matrix
矩阵是一个二维数组,若干个等同维度的向量放在一起就可以看作是一个矩阵,矩阵中的每一个值是一个标量,可以通过行号和列号进行索引
① 矩阵加法
对位相加,需要矩阵的行列相同
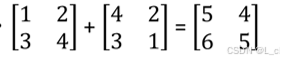
② 矩阵乘法
不满足交换律 A * B != B * A
当左矩阵A的列数等于右矩阵B的行数时,A与B可以相乘
M × N矩阵 乘以 N × P矩阵 得到 M × P维度矩阵
矩阵乘法可以理解为多个向量做向量内积运算
叉乘:卷积神经网络
符合分配律 A * (B + C) = A * B + A * C
符合结合律 A * (B * C) = (A * B) * C
另一种矩阵乘法是矩阵点乘
两矩阵必须形状一致,对位相乘
点乘:Transformer
③ 常见矩阵操作
矩阵转置
行列互换transpose
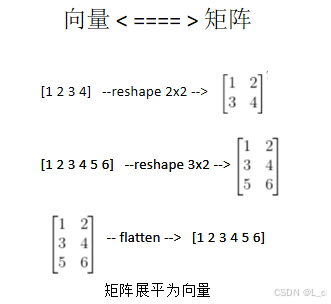
向量与矩阵的互换
矩阵的重塑reshape和展平flatten是为了改变矩阵的形状,使矩阵能够合法参与运算
4.张量 tensor
将多个矩阵叠加在一起
张量是神经网络的训练中最为常见的数据形式
所有的输入,输出,中间结果,几乎都是以张量的形式存在
① 常见张量操作
shape 重塑 transpose 转置 view 展平
矩阵相乘是在做某种意义上的批量运算
二、numpy常用操作
1.Python中矩阵的定义
① 列表(List)
定义方式:在Python中,列表是最常用的用于存储一组数据的数据结构。可以使用方括号 [] 来定义一个列表,列表中的元素可以是不同的数据类型,如整数、浮点数、字符串、甚至是其他列表等。
访问元素:可以通过索引来访问列表中的元素。在Python中,索引是从0开始的。
列表的操作:
修改元素:可以通过索引来修改列表中的元素。
添加元素:可以使用append()方法在列表末尾添加一个元素
插入元素:可以使用insert("元素名")方法在指定位置插入一个元素
删除元素:可以使用remove("元素名")方法删除指定元素、使用pop("索引数")方法删除指定索引位置的元素
'''
修改元素:可以通过索引来修改列表中的元素。
添加元素:可以使用append()方法在列表末尾添加一个元素
插入元素:可以使用insert("元素名")方法在指定位置插入一个元素
删除元素:可以使用remove("元素名")方法删除指定元素、使用pop("索引数")方法删除指定索引位置的元素
'''
my_list = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print(my_list[4])
my_list[4] = 1
print(my_list[4])
my_list.append(4)
print(my_list)
my_list.insert(0, 0)
print(my_list)
my_list.remove(4)
print(my_list)
my_list.pop(0)
print(my_list)
② 数组模块(array)
定义方式:Python的array模块提供了一种更高效的存储同类型数据的数组结构。需要先导入array模块,然后使用array()函数来创建数组。
适用场景:当需要存储大量同类型的数据并且对性能(如内存占用和运算速度)有一定要求时,array模块比普通列表更合适。
③ NumPy数组(ndarray)
定义方式:如果需要进行更高级的数学运算和数据处理,NumPy库中的ndarray(多维数组)是一个很好的选择。首先需要安装NumPy库,然后导入并使用。
优势:
强大的数学运算功能:NumPy提供了大量的数学函数,可以对数组进行高效的数学运算,如加法、乘法、求平均值、标准差等。
支持广播机制:在进行不同形状数组的运算时,NumPy的广播机制可以自动调整数组的形状,使运算能够顺利进行。
高效的存储和计算:对于大规模数据的处理,NumPy数组在内存占用和计算速度上有很大的优势,尤其是在科学计算、数据分析和机器学习等领域。
2.Numpy中矩阵的属性
属性 说明
.ndim 秩,即轴的数量或维度的数量
.shape 对象的尺度,对于矩阵来说,即n行m列
.size 对象的个数,即n * m的值
.dtype 对象的类型
'''
.dim 秩,即轴的数量或维度的数量
.shape 对象的尺度,对于矩阵来说,即n行m列
.size 对象的个数,即n*m的值
.dtype 对象的类型
'''
import numpy as np
my_list = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(my_list)
print(my_list.ndim)
print(my_list.shape)
print(my_list.size)
print(my_list.dtype)3.Numpy中的函数
函数 说明
np.arange(n) 类似range函数,返回ndarray类型,元素从0 到 n - 1
np.ones(shape) 根据shape生成一个全1数组,shape是元组类型
np.zeros(shape) 根据shape生成一个全0数组,shape是元组类型
np.full(shape,val) 根据shape生成一个数组,每个元素值都为val
np.eye(n) 创建一个正方的n * n的单位矩阵,对角线全为1其余为0
np.linspace(b,e,n) 根据起始值等间距的填充数据,形成数组
np.abs(x) 计算数值各数的绝对值,参数随意,返回值类型和输入参数类型相同
np.fabs(x) 计算数值各数的绝对值,参数只适用浮点数和整数类型,返回值类型总是浮点数
np.sqrt(x) 计算数组各元素的平方
np.square() 计算数组各元素的平方根
np.log(x) 计算各元素的自然对数
np.log10(x) 计算各元素的10底对数
np.log2(x) 计算各元素的2底对数
np.ceil(x) 向上取整
np.floor(x) 向下取整
np.rint(x) 四舍五入
np.modf(x) 将各元素的小数和整数部分以两个独立的数组形式返回
np.cos(x) 计算数组中每个元素的余弦值
np.cosh(x) 计算数组中每个元素的双曲余弦值
np.sin(x) 计算数组中每个元素的正弦值
np.sinh(x) 计算数组中每个元素的双曲正弦值
np.tan(x) 计算数组中每个元素的正切值
np.tanh(x) 计算数组中每个元素的双曲正切值
np.exp(x) 各元素x次幂
np.sign(x) 计算各元素的符号值:1(+)、0(0)、-1(-)
sum(a,axis=None) 根据给定轴axis计算数组a相关元素之和,axis为整数或元组
mean(a,axis=None) 计算期望
average(a,axis=None,weights=None) 计算加权平均值
std(a.axis=None) 计算标准差
var(a,axis=None) 计算方差
min(a), max(a) 计算数组a中的最小值,最大值
ptp(a) 计算数组a中最大值与最小值的差
median(a) 计算中位数. reshape(shape) 不改变数组元素,返回一个shape形状的数组,但原数组不变
resize(shape) 与.reshape()功能一致,但修改原数组
swapaxes(ax1.ax2) 将数组n个维度中两个进行交换
flatten() 对数组进行降维,返回折叠后的一维数组,原数组不变
rand(d0,d1....dn) 根据d0-dn创建随机数数组,浮点数,[0,1),均匀分布
randn(d0,d1....dn) 根据d0-dn创建随机数组,标准正态分布
randint(low,high,shape) 根据shape创建随机整数或数组,范围是[low,high)
seed(s) 随机数种子,s是给定的种子值,作用:使得随机数据可预测,即设置了相同的随机数种子,生成的这三个随机矩阵的内容都将是固定不变的
import numpy as np
# np.arange(n) 类似range函数,返回ndarray类型,元素从0 到 n - 1
my_list = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(f"arange:\n{np.arange(0, 8)}")
print("———————————————————————————————————————————————————————————————————")
# np.ones(shape) 根据shape生成一个全1数组,shape是元组类型
my_list = np.ones((3, 3))
print(f"ones:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.zeros(shape) 根据shape生成一个全0数组,shape是元组类型
my_list = np.zeros((3, 3))
print(f"zeros:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.full(shape,val) 根据shape生成一个数组,每个元素值都为val
my_list = np.full((4, 4), 4)
print(f"full:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.eye(n) 创建一个正方的n * n的单位矩阵,对角线全为1其余为0
my_list = np.eye(3)
print(f"eye:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.linspace(b,e,n) 根据起始值等间距的填充数据,形成数组
my_list = np.linspace(0, 11, 5)
print(f"linspace:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.abs(x) 计算数值各数的绝对值,参数随意,返回值类型和输入参数类型相同
my_list = np.abs([-1, 0, 1])
print(f"abs:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.fabs(x) 计算数值各数的绝对值,参数只适用浮点数和整数类型,返回值类型总是浮点数
my_list = np.fabs([-1, 0, 1])
print(f"fabs:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.sqrt(x) 计算数组各元素的平方
my_list = np.sqrt([1, 4, 9])
print(f"sqrt:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.square() 计算数组各元素的平方根
my_list = np.square([1, 4, 9])
print(f"square:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.log(x) 计算各元素的自然对数
my_list = np.log([1, 4, 9])
print(f"log:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.log10(x) 计算各元素的10底对数
my_list = np.log10([1, 4, 9])
print(f"log10:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.log2(x) 计算各元素的2底对数
my_list = np.log2([1, 4, 9])
print(f"log2:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.ceil(x) 向上取整
my_list = np.ceil([1.1, 2.1, 3.1])
print(f"ceil:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.floor(x) 向下取整
my_list = np.floor([1.1, 2.1, 3.1])
print(f"floor:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.rint(x) 四舍五入
my_list = np.rint([3.6, 3.7, 4.3, 4.1])
print(f"rint:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.modf(x) 将各元素的小数和整数部分以两个独立的数组形式返回
my_list = np.modf([3.6, 3.7, 4.3, 4.1])
print(f"modf:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.cos(x) 计算数组中每个元素的余弦值
my_list = np.cos([3.6, 3.7, 4.3, 4.1])
print(f"cos:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.cosh(x) 计算数组中每个元素的双曲余弦值
my_list = np.cosh([3.6, 3.7, 4.3, 4.1])
print(f"cosh:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.sin(x) 计算数组中每个元素的正弦值
my_list = np.sin([3.6, 3.7, 4.3, 4.1])
print(f"sin:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.sinh(x) 计算数组中每个元素的双曲正弦值
my_list = np.sinh([3.6, 3.7, 4.3, 4.1])
print(f"sinh:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.tan(x) 计算数组中每个元素的正切值
my_list = np.tan([3.6, 3.7, 4.3, 4.1])
print(f"tan:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.tanh(x) 计算数组中每个元素的双曲正切值
my_list = np.tanh([3.6, 3.7, 4.3, 4.1])
print(f"tanh:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.exp(x) 各元素的x次幂
my_list = np.exp([3.6, 3.7, 4.3, 4.1])
print(f"exp:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# np.sign(x) 计算各元素的符号值:1(+)、0(0)、-1(-)
my_list = np.sign([3.6, 3.7, 4.3, 4.1])
print(f"sign:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# sum(a,axis=None) 根据给定轴axis计算数组a相关元素之和,axis为整数或元组
my_list = np.sum([1, 2, 3, 4, 5, 6, 7, 8, 9], axis=0)
print(f"sum:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# mean(a,axis=None) 计算期望
my_list = np.mean([1, 2, 3, 4, 5, 6, 7, 8, 9], axis=0)
print(f"mean:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# average(a,axis=None,weights=None) 计算加权平均值
my_list = np.average([1, 2, 3, 4, 5, 6, 7, 8, 9], axis=0)
print(f"average:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# std(a.axis=None) 计算标准差
my_list = np.std([1, 2, 3, 4, 5, 6, 7, 8, 9], axis=0)
print(f"std:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# var(a,axis=None) 计算方差
my_list = np.var([1, 2, 3, 4, 5, 6, 7, 8, 9], axis=0)
print(f"var:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# min(a), max(a) 计算数组a中的最小值、最大值
my_list = np.min([1, 2, 3, 4, 5, 6, 7, 8, 9])
print(f"min:\n{my_list}")
my_list = np.max([1, 2, 3, 4, 5, 6, 7, 8, 9])
print(f"max:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# ptp(a) 计算数组a中最大值与最小值的差
my_list = np.ptp([1, 2, 3, 4, 5, 6, 7, 8, 9])
print(f"ptp:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# median(a) 计算中位数
my_list = np.median([1, 2, 3, 4, 5, 6, 7, 8, 9])
print(f"median:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# reshape(shape) 不改变数组元素,返回一个shape形状的数组,但原数组不变
my_list = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
my_list_new = np.reshape(my_list, (3, 3))
print(f"mylist:\n{my_list}")
print(f"reshape:\n{my_list_new}")
print("———————————————————————————————————————————————————————————————————")
# resize(shape) 与.reshape()功能一致,但修改原数组
my_list = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
my_list_new = np.resize(my_list, (3, 3))
print(f"mylist:\n{my_list}")
print(f"resize:\n{my_list_new}")
print("———————————————————————————————————————————————————————————————————")
# swapaxes(ax1.ax2) 将数组n个维度中两个进行交换
my_list = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(f"mylist:\n{my_list}")
my_list_new = np.swapaxes(my_list, 0, 1)
print(f"swapaxes:\n{my_list_new}")
print("———————————————————————————————————————————————————————————————————")
# flatten() 对数组进行降维,返回折叠后的一维数组,原数组不变
my_list = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
my_list_new = my_list.flatten()
print(f"mylist_new:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# rand(d0,d1....dn) 根据d0-dn创建随机数数组,浮点数,[0,1),均匀分布
my_list = np.random.rand(3, 3)
print(f"rand:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# randn(d0,d1....dn) 根据d0-dn创建随机数组,标准正态分布
my_list = np.random.randn(3, 3)
print(f"randn:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# randint(low,high,shape) 根据shape创建随机整数或数组,范围是[low,high)
my_list = np.random.randint(1, 10, (3, 3))
print(f"randint:\n{my_list}")
print("———————————————————————————————————————————————————————————————————")
# seed(s) 随机数种子,s是给定的种子值,作用:使得随机数据可预测,即只要s的值一样,后续生成的随机数都一样
np.random.seed(4)
my_list1 = np.random.randint(0, 10, (3, 3))
print(f"seed 随机整数矩阵1:\n{my_list1}")
my_list2 = np.random.uniform(0, 1, (3, 3))
print(f"seed 随机均匀分布浮点数矩阵:\n{my_list2}")
my_list3 = np.random.normal(0, 1, (3, 3))
print(f"seed 随机正态分布浮点数矩阵:\n{my_list3}")
print("———————————————————————————————————————————————————————————————————")
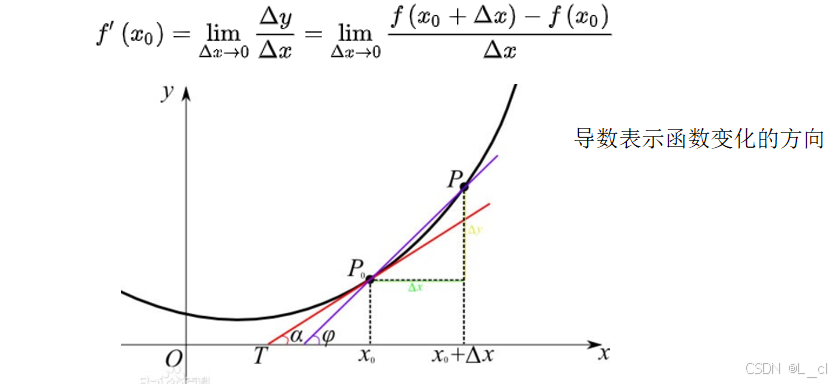
三、导数
导数反映了函数变化的方向