问题描述

小明在二维坐标系中放置了 ( n ) 个点，他想在其中选出一个包含三个点的子集，这三个点能组成三角形。然而这样的方案太多了，他决定只选择那些可以组成等腰三角形的方案。请帮他计算出一共有多少种选法可以组成等腰三角形？

输入格式

输入共 ( n+1 ) 行。

第一行为一个正整数 ( n )。

后面 ( n ) 行，每行两个整数 ( x_i ) 和 ( y_i ) 表示第 ( i ) 个点的坐标。

输出格式

输出共 1 行，一个整数。

样例输入

5
1 1
4 1
1 0
2 1
1 2

样例输出

4

评测用例规模与约定

• 对于 20% 的数据，保证 ( n <= 200)。
• 对于 100% 的数据，保证 ( n <= 2000)，( 0 <= xi, yi <= 1e9)。

题解:

正常的暴力代码👇 时间复杂度O(n^3) 会超时, 只过了不到一半数据

#include <bits/stdc++.h>
using namespace std;
#define int double

const signed N = 1e4;

int a[N], b[N];

signed main()
{
	signed n; cin >> n;
	for (signed i = 0; i < n; i ++) cin >> a[i] >> b[i];
	
	int cnt = 0;
	for (signed i = 0; i < n; i ++)
		for (signed j = i + 1; j < n;  j ++)
			for (signed k = j + 1; k < n; k ++)
			{
				int x1 = sqrt((a[i] - a[j]) * (a[i] - a[j]) + (b[i] - b[j]) * (b[i] - b[j]));
				int x2 = sqrt((a[j] - a[k]) * (a[j] - a[k]) + (b[j] - b[k]) * (b[j] - b[k]));
				int x3 = sqrt((a[i] - a[k]) * (a[i] - a[k]) + (b[i] - b[k]) * (b[i] - b[k]));
				if (x1 + x2 > x3 && x1 + x3 > x2 && x2 + x3 > x1)
				{
					if (abs(x1 - x2) < 1e-8 && abs(x2 - x3) < 1e-8 && abs(x1 - x3) < 1e-8) continue;  // 等边三角形不算， 也可以不写, 因为题中要求横纵坐标都是整数, 那么不可能构成等边三角形
					if (abs(x1 - x2) < 1e-8 || abs(x2 - x3) < 1e-8 || abs(x1 - x3) < 1e-8)  // double 类型判断是否相同要用差来判断, double类型的变量在计算机中存储的值会丢失精度, 不能直接用==
						cnt ++;
				}
			}
			
	cout << cnt << endl;
	return 0;
}

ac代码

这题的思路是尽可能优化时间复杂度,

• 我们枚举每个点, 然后对该点生成一个hash表, 把到该点距离相同的点放到一个数组中, 然后遍历这个hash表中的所有数组,任选数组中的两个点, 判断这三个点是否满足条件

ac代码👇 这个的时间复杂度是在O(n^2) 和 O(n^3)之间的

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define x first
#define y second
typedef pair<int, int> PII;
const double cha = 1e-8;
vector<PII> v;

double dist(int x1, int y1, int x2, int y2)
{
	return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}

bool check(PII a, PII b, PII c)
{
	double x1 = dist(a.x, a.y, b.x, b.y);
	double x2 = dist(a.x, a.y, c.x, c.y);
	double x3 = dist(b.x, b.y, c.x, c.y);
	
	if (x1 + x2 <= x3 || x1 + x3 <= x2 || x2 + x3 <= x1) return false;  // 不能构成三角形
	if (abs(x1 - x2) < cha && abs(x1 - x3) < cha && abs(x2 - x3) < cha) return false;  // 是等边三角形。也可以不写, 因为题中要求横纵坐标都是整数, 那么不可能构成等边三角形
	
	return true;
}

signed main()
{
	int n; cin >> n; v.resize(n);
	
	for (int i = 0; i < n; i ++) cin >> v[i].x >> v[i].y;
	
	int cnt = 0;
	
	for (int i = 0; i < n; i ++)
	{
		unordered_map<double, vector<int>> mp;  // 选用i为一个点的前提下, 其他点到i距离相同的点存放到一个 vector中
		for (int j = 0; j < n; j ++)
		{
			if (i == j) continue;
			double dis = dist(v[i].x, v[i].y, v[j].x, v[j].y);  // 计算距离
			mp[dis].emplace_back(j);  
		}
		
		for (auto it : mp)
		{
			vector<int> vv;
			vv = it.second;  // vv 是到i距离相同的点的 集合, 也就是说vv中的元素都是到i的距离相同的点
			for (int j = 0; j < vv.size(); j ++)
				for (int k = j + 1; k < vv.size(); k ++)
				{
					if (check(v[i], v[vv[j]], v[vv[k]])) cnt ++;  // 因为vv里面存的是下标, 所以是 v[vv[j]]
				}
		}
		
	}
	cout << cnt << endl;
	return 0;
}

下面是笔者自己理解的ac代码的时间复杂度的分析

hash时间复杂度分析:

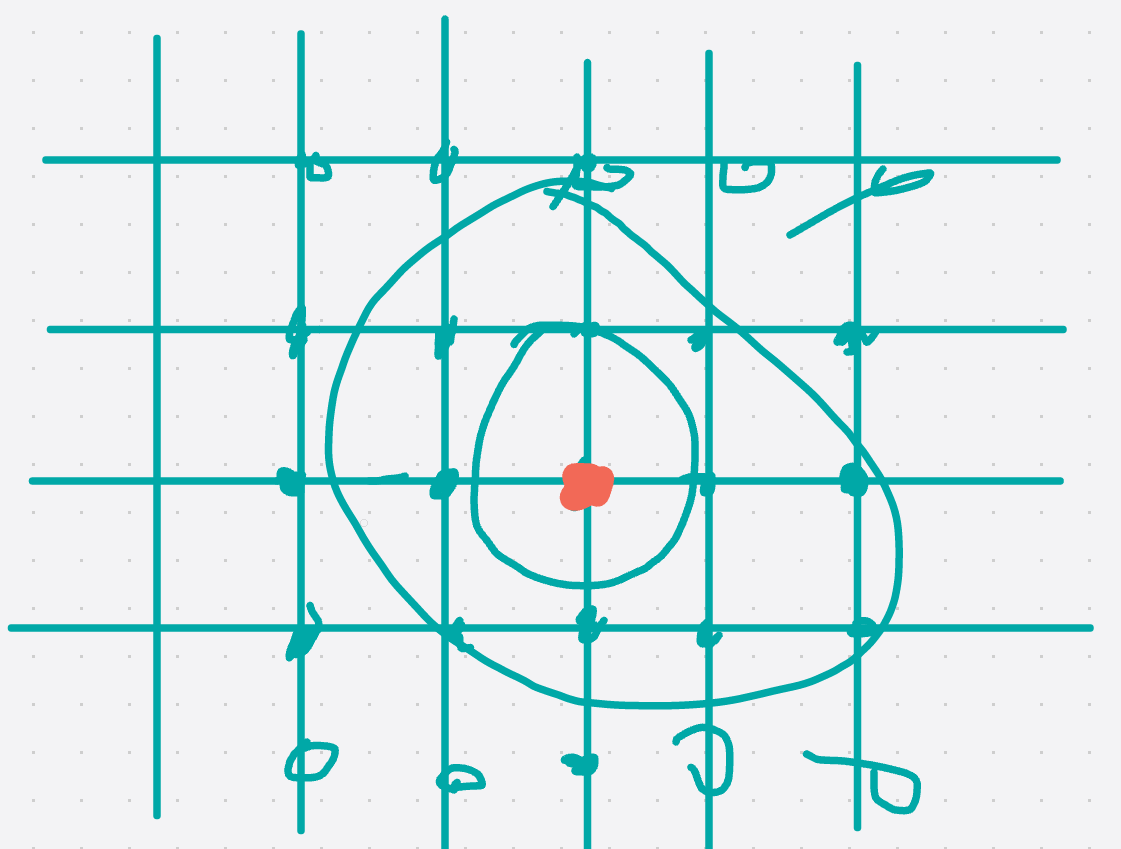
中间的点在执行hash时是最耗时的, 而且图中这种方式的点分布也是让所有点的时间复杂度尽可能多的情况。

下面分别是vector的个数和map个数分析

• 因为坐标的横纵坐标都只能是整数, 所有一个 map映射的vector中最多有4个数, 也就是说距离到i坐标相同的点最多有4个, 上下左右距离相同 4个, 4个对焦的点距离相同.

• 而map映射的个数是 中间的点的最外围每增加一圈, map映射的个数加2, 因为每增加一圈 横纵的距离+1, 斜线的距离+根号2， 一共是两种

hash执行总次数 m 和总个数 n 之间的大小关系分析

当点的个数增加到2000的时候, 实际hash执行的次数不到2000 (map的映射个数不到 100,(这里按50个外圈, 50 * 50是2500个点的个数, 比2000个点大), vecotr中最多是4个点, 4 * 4 = 16) 所以hash执行的次数是100 * 16 == 1600, 这还是中间点的情况, 而且是按2500个点算, 其他点的遍历次数更少 ( m < n )

还有就是, 从上面的分析可以看到, 点的个数越小, 遍历hash的总次数有可能反而比 n 次还要多, 但是当点的个数n边大的时候, 遍历hash的总次数会比(n - 1)小很多。------> 比如一共9个点, 3*3, 中间的点正常应该遍历(n - 1) = 8次, 但是用hash的话应该遍历了 2 * (4 * (4 - 1) / 2) = 12次, 2是hash的两个映射 距离为1和距离为根号2, 4是距离为1和根号2的vector中各有4各元素 。(ps:代码中的for ( int j = 0; j < vv.size(); j ++);for (int k = j + 1; k < vv.size(); k ++) 时间复杂度是(n * (n - 1) / 2)

总的时间复杂度

当点的个数比较大的时候, O(n * (n + m)), m < n, 时间复杂度很OK
即使当点的个数n比较小的时候m可能比n大, 但无伤大雅, 因为它不会比n大特别多,而且也说了 n 比较小这个前提, 这个ac代码的时候复杂度可以看成是O(n^2)

觉得写的不错的话, 点个赞吧~