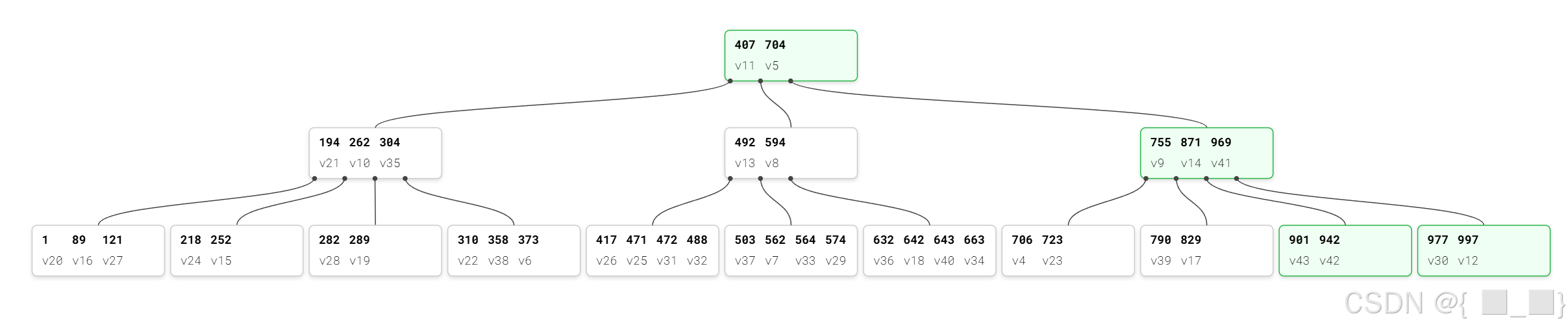
从二叉查找树到B+树的演进
通过对比二叉查找树、平衡二叉树、B树和B+树,从简单到复杂,逐步帮助理解B+树的特点及优势。
1. 二叉查找树(Binary Search Tree, BST)
二叉查找树是一种简单的树结构,特点是每个节点最多有两个子节点:
- 左子树:所有节点值小于根节点。
- 右子树:所有节点值大于根节点。
特点
- 查询时间复杂度:
- 平均情况:(O(log n))
- 最差情况:(O(n))(当树退化为链表时)
- 数据存储位置:数据存储在每个节点中。
示例图
10
/ \
5 20
/ \ \
3 7 30
缺点
- 树容易变得不平衡,影响查询效率。
2.平衡二叉树(Balanced Binary Tree, AVL Tree)
平衡二叉树在二叉查找树的基础上,通过旋转操作保持树的平衡。
特点
- 始终保持查询复杂度为
- O(log n)
- 数据存储位置:和二叉查找树相同,数据存储在每个节点中。
- 插入和删除操作时,可能需要通过旋转来维持平衡。
示例图
10
/ \
5 20
/ \ / \
3 7 19 30
缺点
- 对频繁插入/删除操作不友好,调整成本高。
3.B树(B-Tree)
B树是多路平衡树,特点是每个节点可以存储多个键值。
B树的阶数m:每个节点最多包含 m-1 个键值,最多有 m 个子节点。
特点
- 树高度较低:相比二叉树,B树每个节点存储多个键值,减少树的高度。
- 数据存储分布:数据存储在非叶子节点和叶子节点中。
- 磁盘优化:每个节点通常对应一个磁盘页,减少磁盘I/O。
缺点
- 数据存储在非叶子节点和叶子节点中,范围查询效率不如B+树。
4.B+树(B+ Tree)
B+树是对B树的进一步优化:
- 非叶子节点:只存储键值,用于索引。
- 叶子节点:存储所有数据,并按照大小顺序排列,叶子节点之间用链表连接。
特点
- 查询效率:时间复杂度为(O(log n))
- 数据存储分布:
- 非叶子节点:只存储键值,用于索引。
- 叶子节点:存储所有数据,并按顺序排列。
- 磁盘优化:节点存储多个键值,充分利用磁盘页预读特性。
- 适用场景:数据库索引、文件系统等。
| 特性 | 二叉查找树 | 平衡二叉树 | B树 | B+树 |
|---|---|---|---|---|
| 树的阶数 | 2 | 2 | m > 2 | m > 2 |
| 节点存储 | 1个键值 | 1个键值 | 多个键值 | 多个键值 |
| 数据存储位置 | 所有节点 | 所有节点 | 所有节点 | 仅叶子节点 |
| 范围查询效率 | 不高 | 不高 | 较高 | 非常高 |
| 树的高度 | 较高 | 较高 | 较低 | 最低 |
| 适用场景 | 内存中简单查找 | 内存中高效查找 | 数据库、磁盘系统 | 数据库、文件系统优化 |
每层节点的存储能力
- 根节点:存储 1000 个键值,可以指向 1001 个子节点。
- 中间节点:每个节点可以存储 1000 个键值,并指向 1001 个下一层节点。
- 叶子节点:最终存储实际数据,每个节点可以存储 1000 条记录。
3层 B+树的计算
- 第一层(根节点):根节点最多可以指向1000个键值(节点数)。
- 第二层(中间层):每个中间节点又可以指向1000个键值,总共有1000×1000=
1,000,000个键值(节点数)。 - 第三层(叶子节点):叶子节点每个可以存储1000条实际数据,总共有1000×1000×
1000=1,000,000,000条数据。
3层 B+树的存储总量
3层 B+树的存储总量就是叶子节点的总存储量,所以这里的计算结果是 10亿条数据。