A. Submission Bait（博弈）

题意：爱丽丝和鲍勃在大小为n的数组a中进行游戏，他们轮流进行运算，爱丽丝先开始，不能运算的一方输，一开始mx=0，每次操作，玩家可以选择一个牵引i，ai>=mx，mx设置为ai，ai设为0.判断爱丽丝是否有一个获胜策略。

分析：只要一个数出现奇数个，那么爱丽丝就可以先手拿走那出现奇数个的数的最大值，从这个数到数组最大值都是剩下偶数个，无论鲍勃怎么拿，爱丽丝都能取走最后一个并获得胜利。

代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t; cin>>t;
    while(t--){
        int n; cin>>n;
        map<int,int>mp;
        for(int i=1;i<=n;i++){
            int x;cin>>x;
            mp[x]++;
        }
        int cnt=1;
        for(auto &x:mp){
            if(x.second%2==1){
                cnt=0;
                break;
            }
        }
        if(!cnt)cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    return 0;
}

B. Array Craft（构造，贪心）

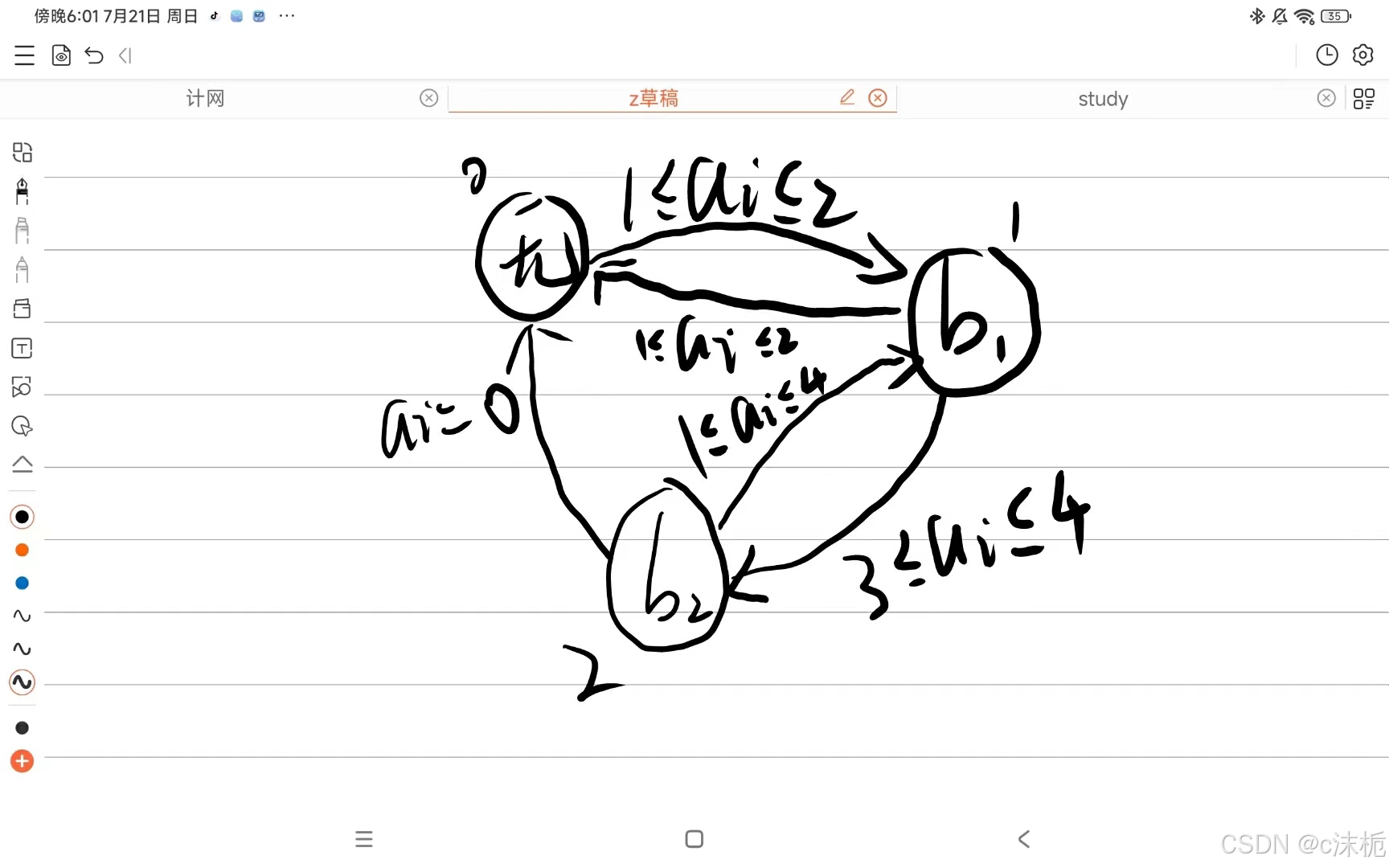
题意：对于长度为m的数组b可以定义：(j为数组任意下标)

b的最大前缀位置是b1+...bi=max(b1+...+bj)的最小牵引i

b的最大后缀位置是bi+....bm=max(bj+...+bm)的最大牵引i

现在给三个整数，n，x，y，构造一个数组满足：

对于所有1<=i<=n，ai要么是1要么是-1

a的最大前缀位置是x，a的最大后缀位置是y。

分析：因为y<x,可以分成三部分,[1,y-1],[y,x],[x+1,n]，可以让第一部分等于-1，这样不会对后缀和最大值有影响，第三部分等于-1，这样不会对前缀和产生影响，让中间部分都等于1.

代码：

#include<bits/stdc++.h>
using namespace std;
void sol(){
    int n,x,y;cin>>n>>x>>y;
    for(int i=1;i<=n;i++){
        int a;
        if(i<y)a=(y-i)%2==0?1:-1;
        else if(i<=x)a=1;
        else a=(i-x+1)%2==0?-1:1;
        cout<<a<<" ";
    }
    cout<<endl;
}
int main(){
    int t;cin>>t;
    while(t--)sol();
    return 0;
}

C. Mad MAD Sum（贪心）

题意：定义MAD为数组中至少出现两次的最大数字，如果没有就是0.给定一个长度为n的数组a，sum=0，下面的过程将依次循环执行，直到a中的所有数字都变成0：

设置sum+=∑ai；设bi=MAD（a1,a2..ai),ai=bi

求过程结束后sum的值。

分析：经历操作一次后的数组是非递减的，以后每次都是将数组向右移动，为了防止数组从左往右，不含0的第一个数字在数组里只出现1此，我们可以再执行一次操作，所以只要执行两次操作就能知道剩下的操作次数。

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+10;
bool c[N];
ll n,a[N];
void g(){
    for(ll i=1;i<=n;i++)c[i]=false;
    ll ma=0;
    for(ll i=1;i<=n;i++){
        if(c[a[i]])ma=max(ma,a[i]);
        c[a[i]]=true;
        a[i]=ma;
    }
}
void sol(){
    cin>>n;
    ll ans=0;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        ans+=a[i];
    }
    g();
    for(ll i=1;i<=n;i++)ans+=a[i];
    g();
    for(ll i=1;i<=n;i++){
        ans+=(n-i+1)*a[i];
    }
    cout<<ans<<endl;
}
int main(){
    int t;cin>>t;
    while(t--)sol();
    return 0;
}

D. Grid Puzzle

题意：给定一个数组，有一个nn的网格。在第i行，从第一个到第ai个都是黑格子，剩下的是白格子。可以进行以下操作：将2×2子网格染白；将整行染白。找出将所有单元格染白的最少操作次数。

分析：如果ai>=5我们会想使用操作2，因为至少需要三个2×2的子网覆盖它，第i-1和i+1行不一定是黑格子，所以有可能浪费了。先考虑ai<=4的情况。

只右三种情况：不受上一行影响；涂前两格：涂后两格。

代码：（贪心）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
void sol(){
    int n;cin>>n;int a[n+10];
    for(int i=1;i<=n;i++)cin>>a[i];
    bool b1=0,b2=0;ll ans=0;
    for(int i=1;i<=n;i++){
        if((!b1)&&(!b2)){
            if(a[i]==0)continue;
            ans++;
            if(a[i]<=2)b1=1;
        }
        else if(b1){
            b1=0;
            if(a[i]<=2)continue;
            ans++;
            if(a[i]<=4)b2=1;
        }
        else{
            b2=0;
            if(a[i]==0)continue;
            ans++;
            if(a[i]<=4)b1=1;
        }
    }
    cout<<ans<<endl;
}
int main(){
    int t;cin>>t;
    while(t--)sol();
    return 0;
}

（dp）

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int a[N],dp[N];
void sol(){
    int n;cin>>n;
    int b[2]={N,N};
    for(int i=1;i<=n;i++)cin>>a[i];
    //b0=N，b1=N就是对下一行无影响
    for(int i=1;i<=n;i++){
        dp[i]=dp[i-1]+1;
        if(a[i]==0)dp[i]=min(dp[i],dp[i-1]);
        if(a[i]<=2)dp[i]=min(dp[i],i+b[1-i%2]);//上一个位置在奇数，现在在偶数，就可以减去1.反之一偶一奇也可以
        if(a[i]<=2)b[i%2]=min(b[i%2],dp[i-1]-i);
        else if(a[i]>4)b[0]=b[1]=N;
    }
    cout<<dp[n]<<endl;
}
int main(){
    int t;cin>>t;
    while(t--)sol();
    return 0;
}